3.5: MOS-режими

Last updated
Save as PDF

Page ID: 34482

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

CNX йде на пенсію! Підручники OpenStax завжди будуть доступні на сайті openstax.org. Створений спільнотою вміст залишатиметься доступним до серпня 2022 року, а потім буде переміщений до Інтернет-архіву. Дізнатися більше тут

Остаточне рівняння розділу 3.4 дуже схоже на\(I \text{-} V\) характеристики резистора! \(I_{d}\)просто пропорційно напрузі стоку\(V_{\text{ds}}\). Константа пропорційності залежить від габаритів пристрою,\(W\) причому\(L\), як вони інтуїтивно повинні. Струм збільшується, коли транзистор стає ширшим; він зменшується, коли транзистор стає довшим. Це також залежить\(c_{\text{ox}}\) і від\(\mu_{s}\), і від різниці між напругою затвора і пороговим напругою\(V_{T}\). Зверніть увагу, що якщо ми\(V_{\text{gs}}\) скоригуємо, ми можемо змінити нахил\(I \text{-} V\) кривої. Ми зробили резистор, керований напругою!

Малюнок\(\PageIndex{1}\):\(I\text{-}V\) Графік MOSFET в лінійному режимі

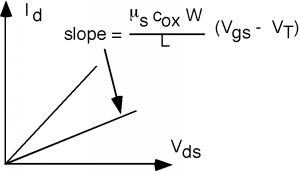
Графік I_D проти V_DS, у першому квадранті. Графік приймає форму прямої, що проходить через початок, з нахилом, рівним добутку mu_s, c_ox і W, поділеної на L, ціле помножене на різницю між v_GS і V_T. — Малюнок\(\PageIndex{1}\):\(I\text{-}V\) Графік MOSFET в лінійному режимі

Однак з цим результатом рекомендується обережність, оскільки ми пропустили щось досить важливе. Повернемося до нашої картини затвора і акумуляторів, що беруть участь в роботі МОП-транзистора. Тут ми явно показали канал як чорну смугу, і ми ввели нову величину\(V_{c} (x)\), напругу вздовж каналу та координату\(x\), яка говорить нам, де ми знаходимося на каналі щодо джерела та стоку. Зверніть увагу, що як тільки ми застосуємо потенціал джерела зливу\(V_{\text{ds}}\), потенціал в каналі\(V_{c} (x)\) змінюється з відстанню уздовж каналу. На кінці джерела,\(V_{c}(0) = 0\) як джерело заземлений. У зливному кінці,\(V_{c}(L) = V_{\text{ds}}\). Визначимо напругу\(V_{\text{gc}}\), яка є різницею потенціалів між напругою затвора і напругою в каналі. \[V_{\text{gc}} (x) \equiv V_{\text{gs}} - V_{c} (x)\]

Таким чином,\(V_{\text{gc}}\) йде від\(V_{\text{gs}}\) вихідного кінця до\(V_{\text{gs}} - V_{\text{ds}}\) зливного кінця.

Малюнок\(\PageIndex{2}\): Вплив\(V_{\text{ds}}\) на потенціал каналу

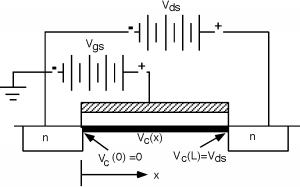
Зміщений MOSFET транзистор з джерелом зліва і стоком праворуч. Напруга каналу між витоком і стоком - функція х, відстань від лівого краю каналу. При x=0 напруга каналу дорівнює 0; при x=L, на правому краю каналу напруга каналу V_DS. — Малюнок\(\PageIndex{2}\): Вплив\(V_{\text{ds}}\) на потенціал каналу

Чиста щільність заряду в каналі залежить від різниці потенціалів між затвором і каналом в кожній точці вздовж каналу, а не тільки\(V_{\text{gs}} - V_{T}\). Таким чином, ми повинні змінити рівняння іншого модуля, щоб врахувати це. \[\begin{array}{l} Q_{\text{chan}} &= c_{\text{ox}} \left(V_{\text{gc}} (x) - V_{T}\right) \\ &= c_{\text{ox}} \left(V_{\text{gs}} - V_{c} (x) - V_{T}\right) \end{array}\]

Це, в свою чергу, змінює інтегральне співвідношення між\(I_{d}\) і\(V_{\text{gs}}\). \[\int\limits_{0}^{V_{\text{ds}}} \mu_{s} c_{\text{ox}} \left(V_{\text{gs}} - V_{T} - V_{c}(x) \right) W \ dV_{c} (x) = \int\limits_{0}^{L} I_{d} \ dx\]

\(\PageIndex{3}\)Рівняння лише трохи складніше інтегрувати, ніж раніше, і ми отримуємо за струм стоку\[I_{d} = \frac{\mu_{s} c_{\text{ox}} W}{L} \left( \left(V_{\text{gs}}-V_{T}\right) V_{\text{ds}} - \frac{V_{\text{ds}}{ }^2}{2} \right)\]

Це рівняння називається рівнянням Саха після C.T. Sah, який вперше описав роботу МОП-транзистора таким чином ще в 1964 році. Це дуже важливо, оскільки описує основну поведінку МОП-транзистора.

Зауважте\(V_{\text{ds}}\), що для малих значень попереднього рівняння та рівняння\(\PageIndex{4}\) дадуть нам таку ж\(I_{d} \text{-} V_{\text{ds}}\) поведінку, оскільки ми можемо ігнорувати\(V_{\text{ds}}{ }^2\) термін у Рівнянні\(\PageIndex{4}\). Це називається лінійним режимом, оскільки ми маємо пряму залежність між струмом стоку та напругою сток-джерело. Як\(V_{\text{ds}}\) починає збільшуватися, однак, квадрат термін почне штовхнути, і сюжет почне перегинатися. Очевидно, що щось призводить до того, що струм падає, коли\(V_{\text{ds}}\) стає більшим. Це пояснюється тим, що різниця напруг між затвором і каналом стає менше, а це означає, що в каналі менше заряду для забезпечення провідності. Ми можемо графічно показати це, зробивши шар каналу більш тонким, коли ми рухаємося від джерела до стоку. Рівняння\(\PageIndex{4}\), і насправді, Рисунок\(\PageIndex{3}\) змусить нас думати, що якщо\(V_{\text{ds}}\) стає досить великим, що струм стоку\(I_{d}\) повинен фактично почати зменшуватися знову, і, можливо, навіть стати негативним! Це здається не дуже інтуїтивним, тому давайте більш детально розберемося в тому місці, де\(I_{d}\) стає максимум. Ми можемо визначити\(V_{\text{d sat}}\) як напругу джерела-стоку, де\(I_{d}\) стає максимальним. Ми можемо знайти це, взявши\(I_{d}\) похідну щодо\(V_{\text{ds}}\) та встановивши похідну\(0\). \[\begin{array}{l} \frac{d}{d V_{\text{ds}}} \left(I_{d}\right) &= 0 \\ &= \frac{\mu_{s} c_{\text{ox}} W}{L} \left(V_{\text{gs}} - V_{T} - V_{\text{d sat}} \right) \end{array}\]

На скидання констант: \[V_{\text{d sat}} = V_{\text{gs}} - V_{T}\]

Перестановка цього рівняння дає нам трохи більше розуміння того, що відбувається. \[\begin{array}{l} V_{\text{gs}} - V_{\text{d sat}} &= V_{T} \\ &= V_{\text{gc}} (L) \end{array}\]

Малюнок\(\PageIndex{3}\):\(I\text{-}V\) характеристики, що показують перевертання

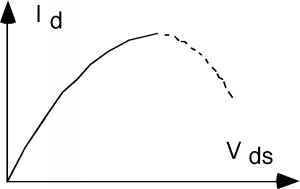
Графік I_D проти V_DS, у першому квадранті. Вигнутий графік приймає форму увігнутої вниз параболи, починаючи з початку, поки не буде досягнуто максимуму параболи; для більших значень v_ds загальна форма параболи триває, але графік розбитий на багато коротких сегментів. — Малюнок\(\PageIndex{3}\):\(I\text{-}V\) характеристики, що показують перевертання

Малюнок\(\PageIndex{4}\): Вплив\(V_{\text{ds}}\) на канал

Перспективний вид прямокутної призми джерела і стоку, розташованих зліва і справа відповідно. Канал між ними представлений у вигляді прямої трикутної призми, причому верхня грань врівень з верхніми гранями витоку і стоку, основа трикутника розташована поруч з витоком, а вершина трикутника торкається верхнього лівого кута стоку. — Малюнок\(\PageIndex{4}\): Вплив\(V_{\text{ds}}\) на канал

На зливному кінці каналу, коли\(V_{\text{ds}}\) просто дорівнює\(V_{\text{d sat}}\), різниця між напругою затвора і напругою каналу,\(V_{\text{gc}} (L)\) якраз дорівнює\(V_{T}\), пороговому напрузі. Будь-яке подальше збільшення\(V_{\text{ds}}\) і різниця між затвором і каналом (в районі каналу трохи біля стоку) опуститься нижче порогового напруги. Це означає, що коли\(V_{\text{ds}}\) стає більше\(V_{\text{d sat}}\), канал просто біля області зливу зникає! У нас більше немає достатньої напруги між затвором і областю каналу для підтримки інверсійного шару, тому ми просто повертаємося до стану виснаження. Це називається відщипнути, як видно на малюнку\(\PageIndex{5}\).

Малюнок\(\PageIndex{5}\): Канал в защемлення

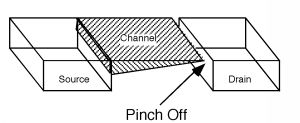
Канал в защемлення: аналогічно малюнку 4 зверху, але з каналом, що не поширюється на весь шлях до зливу. Між стоком і вершиною правотрикутної призми каналу є невеликий зазор. — Малюнок\(\PageIndex{5}\): Канал в защемлення

Що відбувається з струмом стоку, коли ми вдаримо затиснути? Схоже, це може піти на нуль, але це не правильна відповідь! Хоча немає активного каналу в області защемлення, все ще є кремній - він просто виснажується з усіх вільних носіїв. Існує електричне поле, що йде від стоку до каналу, і будь-які електрони, які рухаються по каналу в область защемлення, всмоктуються поперек полем і потрапляють в стік. Це так само, як струм, який протікає в стані зворотного насичення діода. У області виснаження діода немає вільних носіїв, але\(I_{\text{sat}}\) протікає через область з'єднання.

В умовах защемлення, далі збільшується\(V_{\text{ds}}\), не призводить до більшого струму стоку. Ви можете думати про защемлений канал як резистор, з напругою\(V_{\text{d sat}}\) на ньому. Коли\(V_{\text{ds}}\) стає більше\(V_{\text{d sat}}\), надлишкова напруга з'являється в області відключення, а напруга на каналі залишається фіксованою\(V_{\text{d sat}}\). Якщо канал тримає той же заряд, і має на ньому однакове напруга, то струм через канал (і в стік) залишиться фіксованим, за значенням ми зателефонуємо\(I_{\text{d sat}}\).

Є ще одна фігура, яка іноді допомагає бачити, що відбувається. Ми побудуємо потенційну енергію для електрона, коли він проходить через канал. Оскільки джерело знаходиться на нульовому потенціалі, а стік - на\(V_{\text{ds}}\), електрон втратить потенційну енергію, коли вона тече від джерела до стоку. \(\PageIndex{6}\)На малюнку наведено кілька прикладів для різних значень\(V_{\text{ds}}\):

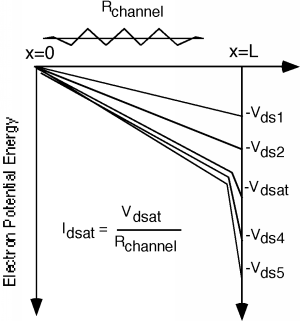
Переходячи від джерела до стоку, потенційна енергія електронів зменшується. Графік приймає форму прямих ліній з відносно неглибокими схилами, що йдуть від 0 до -v_DS1 і -v_DS2; для досягнення значень -v_DSAT, -v_DS4 та -v_DS5, графік має неглибокі ухили для більшої частини довжини каналу перед різким переходом на більш крутий нахил для останньої ділянки. — Малюнок\(\PageIndex{6}\): Падіння енергії потенціалу електрона йде від джерела до стоку.

Для перших двох напруг стоку,\(V_{\text{ds}1}\) і\(V_{\text{ds}2}\), ми знаходимося нижче затискання, і тому падіння напруги через\(R_{\text{channel}}\)\(R_{\text{channel}}\) збільшується, а значить, так і відбувається\(I_{d}\). На\(V_{\text{d sat}}\), ми тільки що досягли pinch-off, і ми починаємо бачити, як «високе поле» виснаження області починають розвиватися. Оскільки електричне поле є лише похідною потенціалу, нахил кривих на малюнку\(\PageIndex{6}\) дає вам уявлення про те, наскільки великим буде електричне поле. Для подальшого збільшення\(V_{\text{ds}}\), таких як\(V_{\text{ds}4}\) і\(V_{\text{ds}5}\) вся додаткова напруга просто з'являється у вигляді високого падіння поля в кінці каналу. Падіння напруги на провідній частині каналу залишається фіксованим (більш-менш) при,\(V_{\text{d sat}}\) і тому струм стоку залишається більш-менш фіксованим\(I_{\text{d sat}}\). Підставивши вираз for\(V_{\text{sat}}\) в вираз for\(I_{d}\), ми можемо отримати вираз для\(I_{\text{d sat}}\):\[I_{\text{d sat}} = \frac{\mu_{s} c_{\text{ox}} W}{2L} \left(V_{\text{gs}} - V_{T}\right)^{2}\]

Ми можемо визначити нову константу\(k\), де\[k = \frac{\mu_{s} c_{\text{ox}} W}{L}\]

Так що \[I_{\text{d sat}} = \frac{k}{2} \left(V_{\text{gs}} - V_{T}\right)^{2}\]

Що це означає для малюнка\(\PageIndex{3}\) є те, що коли\(V_{\text{ds}}\) добирається\(V_{\text{d sat}}\), ми просто тримаємо\(I_{d}\) фіксованою з тих пір, зі значенням\(I_{\text{d sat}}\). Для різних значень\(V_{g}\) напруги затвора ми будемо мати іншу\(I_{d} \text{-} V_{\text{ds}}\) криву, і тому ще раз, ми в кінцевому підсумку з сімейством «характерних кривих» для MOSFET. Вони наведені на малюнку\(\PageIndex{8}\).

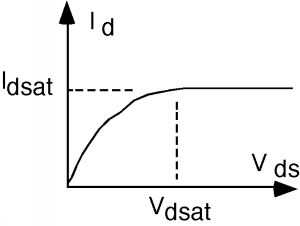
Малюнок\(\PageIndex{7}\): Повна\(I\text{-}V\) крива для MOSFET

Графік I_D проти v_DS, в першому квадранті.Починаючи з початку, графік піднімається в увігнуту вниз параболу, яка плавно переходить до горизонтальної лінії в точці (v_DSAT, I_DSAT). — Малюнок\(\PageIndex{7}\): Повна\(I\text{-}V\) крива для MOSFET

Малюнок\(\PageIndex{8}\): Характеристичні криві для MOSFET

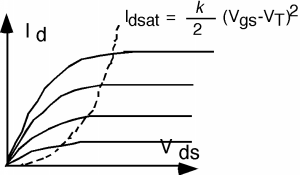
Набір характерних кривих для MOSFET, кожен з яких слідує шаблону кривої з малюнка 7 вище з різною крутизною для початкових кривих і змінними нахилами для пізніших лінійних частин. — Малюнок\(\PageIndex{8}\): Характеристичні криві для MOSFET

Це також дає нам досить простий спосіб «накидати» набір характерних кривих для даного пристрою. Припустимо, у нас є MOS польовий транзистор, який має порогову напругу 2 вольт, ширину 10 мкм і довжину каналу 1 мкм, товщину оксиду 150 ангстрем і поверхневу рухливість\(400 \ \frac{\mathrm{C}}{\mathrm{V} \cdot \mathrm{sec}}\). Використовуючи\(\varepsilon_{\text{ox}} = 3.3 \times 10^{-13} \ \frac{\mathrm{F}}{\mathrm{cm}}\), отримуємо значення\(2.2 \times 10^{-7} \ \frac{\mathrm{F}}{\mathrm{C}}\) for\(c_{\text{ox}}\). Це потім робить\(k\) значення\[\begin{array}{l} k &= \frac{\mu_{s} c_{\text{ox}} W}{L} \\ &= \frac{400 \cdot 2.2 \times 10^{-7} \cdot 10}{1} \\ &= 8.8 \times 10^{-4} \ \frac{\mathrm{amp}}{\mathrm{volt}^2} \end{array}\]