Skip to main content
LibreTexts - Ukrayinska

1.4: Плоскі хвилі

  1. Last updated
  2. Save as PDF
  • Page ID
    31907

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми можемо комбінувати коливання часу та просторової фази, щоб зробити біжить хвилю. Наприклад

    \[ \psi(x,t) = e^{i(k_{0}x-\omega_{0}t)} \nonumber \]

    Визначаємо інтенсивність хвилі як

    \[ |\psi|^{2} = \psi^{*} \psi \nonumber \]

    Де\(\psi^{*}\) знаходиться складний сполучений з\(\psi\). Оскільки інтенсивність цієї хвилі рівномірна скрізь,\(|\psi|^{2} =1\) вона відома як плоска хвиля.

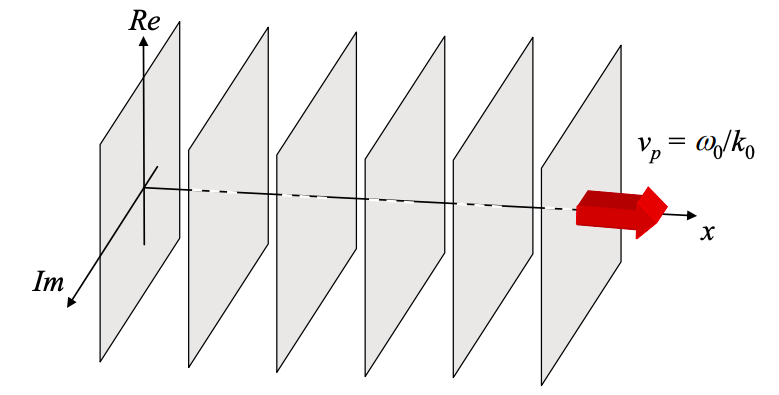
    Плоска хвиля має щонайменше чотири розміри (реальна амплітуда, уявна амплітуда, x та t), тому побудувати графік не так просто. Замість цього на малюнку 1.4.1 ми будуємо площини заданої фази. Ці площини рухаються через простір з\(v_{p}\) фазовою швидкістю хвилі. Для прикладу розглянемо площину, відповідну\(\phi=0\).

    \[ k_{0}x-\omega_{0}t=0 \nonumber \]

    Тепер,

    \[ v_{p} = \frac{dx}{dt} = \frac{\omega_{0}}{k_{0}} \nonumber \]

    Скріншот 2021-04-13 о 21.5.0.png
    Рисунок\(\PageIndex{1}\): У площині хвилі площини постійної фази рухаються через простір з фазовою швидкістю.