Skip to main content
LibreTexts - Ukrayinska

1.3: Огляд класичних хвиль

  1. Last updated
  2. Save as PDF
  • Page ID
    31915

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Хвиля - це періодичне коливання. Зручно описувати хвилі за допомогою комплексних чисел. Для прикладу розглянемо функцію

    \[ \psi (x) = e^{ik_{0}x} \nonumber \]

    де x - позиція, і\(k_{0}\) є константою, відомою як wavenumber. Ця функція побудована на малюнку 1.3.1 на комплексній площині як функція положення, х. фаза функції

    \[ \phi = k_{0}x \nonumber \]

    - кут на складній площині.

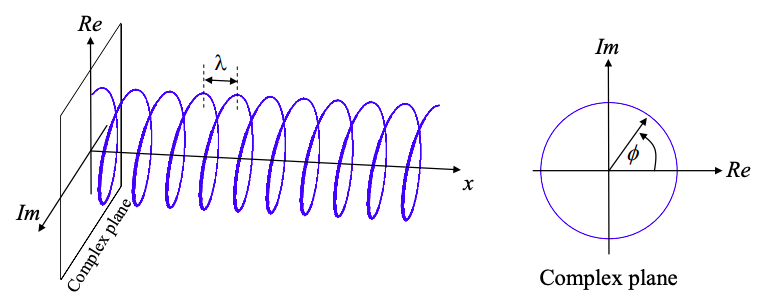
    Знімок екрана 2021-04-13 о 21.36,57.png
    Малюнок\(\PageIndex{1}\): Стояча хвиля з її фазою, нанесеною на складну площину.

    Довжина хвилі визначається як відстань між просторовими повтореннями коливання. Це відповідає фазовій зміні\(2\pi \). З рівнянь 1.3.1 і 1.3.2 отримуємо

    \[ k_{0} = \frac{2\pi}{\lambda} \nonumber \]

    Ця хвиля не залежить від часу, і відома як стояча хвиля. Але ми могли б визначити функцію, фаза якої змінюється з часом:

    \[ \psi(t) = e^{-i\omega_{0}t} \nonumber \]

    Ось t час, і\(\omega\) є кутова частота. Визначимо період, Т, як час між повтореннями коливання

    \[ \omega_{0} = \frac{2\pi}{T} \nonumber \]