6.23: Тонкощі кодування

Цілі навчання

• Деякі тонкощі кодування, включаючи самостійну синхронізацію і порівняння кодів Хаффмана і Морзе.

У коді Хаффмана бітові послідовності, що представляють окремі символи, можуть мати різну довжину, тому індекс бітового потоку m не збільшується в кроці блокування з індексом сигналу, що значиться символом n. Щоб зафіксувати, як часто біти повинні передаватися, щоб не відставати від виробництва символів джерела, ми можемо обчислити лише середні показники. Якщо у нашому вихідному коді середні

$$\overline{B(A)} \nonumber$$ біти/символ і символи виробляються зі швидкістю R, середня швидкість бітів дорівнює

$$\overline{B(A)}R \nonumber$$

і ця величина визначає тривалість бітового інтервалу T.

Вправа$\PageIndex{1}$

Обчисліть співвідношення між T і середнім бітрейтом

$$\overline{B(A)}R \nonumber$$

Рішення

$$T=\frac{1}{\overline{B(A)}R} \nonumber$$

Тонкість вихідного кодування полягає в тому, чи потрібні нам «коми» в бітовому потоці. Коли ми використовуємо нерівну кількість бітів для представлення символів, як приймач визначає, коли символи починаються і закінчуються? Якщо ви створили вихідний код, який вимагав маркер поділу в бітовому потоці між символами, це було б дуже неефективно, оскільки вам по суті потрібен додатковий символ у потоці передачі.

Примітка

Хорошим прикладом цієї потреби є код Морзе: між кожною буквою телеграфу потрібно вставити паузу, щоб повідомити одержувачу, коли виникають межі літер.

Як показано в цьому прикладі, в bitstream не розміщуються коми, але ви можете однозначно розшифрувати послідовність символів з бітового потоку. Хаффман показав, що його (максимально ефективний) код мав властивість prefix: Жоден код символу не починав код іншого символу. Після того, як у вас є властивість prefix, бітовий потік частково самосинхронізується: Після того, як приймач знає, де починається бітовий потік, ми можемо призначити унікальну і правильну послідовність символів для бітового потоку.

Вправа$\PageIndex{1}$

Намалюйте аргумент, який префікс кодування, незалежно від того, походить від коду Хаффмана чи ні, забезпечить унікальне декодування, коли в коді використовується нерівна кількість бітів/символів.

Рішення

Оскільки жодне кодове слово не починається з чужого кодового слова, перше кодове слово, що зустрічається в бітовому потоці, має бути правильним. Зауважте, що ми повинні починати на початку бітового потоку; стрибки в середину не гарантують ідеального декодування. Кінець одного кодового слова і початок іншого може бути кодовим словом, і ми б заблукали.

Однак наявність префіксного коду не гарантує повної синхронізації: Після переходу в середину бітового потоку ми завжди можемо знайти правильні межі символів? Проблема самосинхронізації пом'якшує використання ефективних алгоритмів кодування джерел.

Вправа$\PageIndex{1}$

Покажіть на прикладі, що бітовий потік, створений кодом Хаффмана, не обов'язково самосинхронізується. Коди фіксованої довжини самостійно синхронізуються?

Рішення

Розглянемо бітовий потік... 0110111... взятий з бітового потоку 0|10|110|110|111|... Ми б неправильно декодували початкову частину, потім синхронізували б. Якщо у нас був код фіксованої довжини (скажімо, 00,01,10,11), ситуація набагато гірша. Стрибки в середину призводить до відсутності синхронізації взагалі!

Інша проблема - бітові помилки, викликані цифровим каналом; якщо вони відбуваються (і вони будуть), синхронізація може бути легко втрачена, навіть якщо приймач почав «синхронізувати» з джерелом. Незважаючи на невеликі ймовірності помилки, пропоновані хорошим дизайном набору сигналів та відповідним фільтром, нечаста помилка може спустошити можливість перекладу бітового потоку в символічний сигнал. Потрібні способи зменшення помилок прийому, не вимагаючи, щоб р _е був меншим.

Приклад$\PageIndex{1}$:

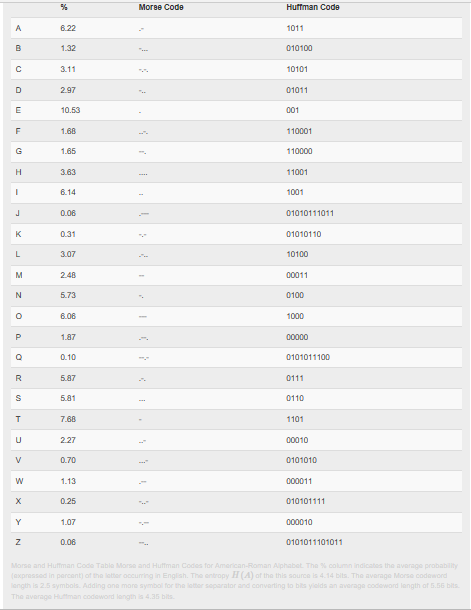
Перша система електричного зв'язку - телеграф - була цифровою. Коли він був вперше розгорнутий у 1844 році, він передавав текст через дротові з'єднання, використовуючи двійковий код - код Морзе - для представлення окремих букв. Щоб надіслати повідомлення з одного місця в інше, телеграфні оператори торкнулися повідомлення за допомогою телеграфного ключа іншому оператору, який би передавав повідомлення наступному оператору, імовірно наближаючи повідомлення до місця призначення. Коротше кажучи, телеграф спирався на мережу, не схожу на основи сучасних комп'ютерних мереж. Сказати, що це передбачало сучасні комунікації, було б заниженням. Він також значно випереджав деякі необхідні технології, а саме теорему кодування джерела. Код Морзе, показаний в таблиці нижче, не був кодом префікса. Щоб розділити коди для кожної літери, код Морзе вимагав, щоб між кожною буквою вставлявся пробіл - пауза. В теорії інформації цей пробіл вважається іншою кодовою літерою, а це означає, що код Морзе закодований текст з трилітерним вихідним кодом: крапками, тире і пробілом. Отриманий вихідний код не знаходиться в межах трохи ентропії і є грубо неефективним (близько 25%). У таблиці наведено код Хаффмана для англійського тексту, який, як ми знаємо, є ефективним.