4.11: Проблеми частотної області

Цілі навчання

• Проблеми, пов'язані з рядами Фур'є.

Прості серії Фур'є

Знайти комплексні зображення рядів Фур'є наступних сигналів без явного обчислення інтегралів Фур'є. Який період сигналу в кожному конкретному випадку?

1. $$s(t)=\sin (t) \nonumber$$
2. $$s(t)=\sin ^{2}(t) \nonumber$$
3. $$s(t)=\cos (t)+2\cos (2t) \nonumber$$
4. $$s(t)=\cos (2t)\cos (t) \nonumber$$
5. $$s(t)=\cos \left ( 10\pi t+\frac{\pi }{6} \right )\left ( 1+ \cos (2\pi t)\right ) \nonumber$$
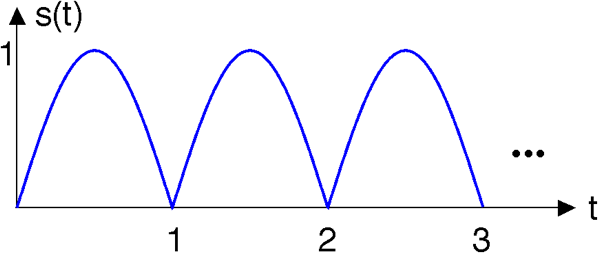
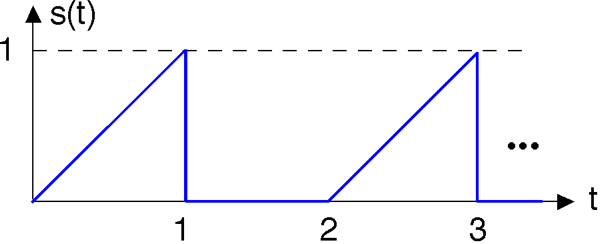
6. s (t), заданий зображеною формою хвилі:

Серія Фур'є

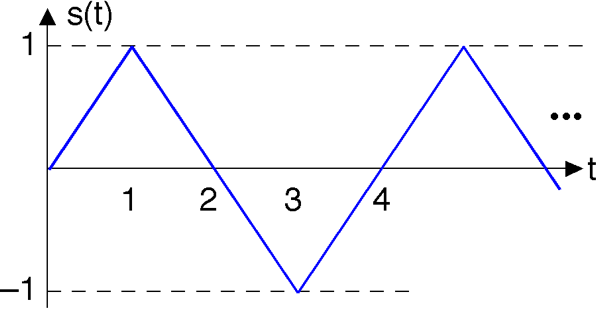
Знайдіть подання рядів Фур'є для наступних періодичних сигналів. Для третього сигналу знайти комплексний ряд Фур'є для хвилі трикутника без виконання звичайних інтегралів Фур'є. Підказка: Як цей сигнал пов'язаний з тим, для якого у вас вже є серія?

1. 
2. 
3. 

Фазові спотворення

Ми можемо дізнатися про фазові спотворення, повернувшись до ланцюгів і досліджуючи наступну схему.

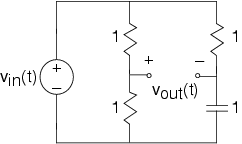
1. Знайдіть функцію перенесення цього фільтра.
2. Знайдіть величину і фазу цієї передавальної функції. Як би ви охарактеризували цю схему?
3. Нехай v _in (t) - квадратна хвиля періоду T. Що таке ряд Фур'є для вихідної напруги?
4. Використовуйте Matlab, щоб знайти форму сигналу вихідного сигналу для випадків T = 0.01 і T = 2. Яке значення T розмежовує два види результатів, які ви знайшли? Програмне забезпечення в fourier2.m може бути корисним.
5. Замість зображеної схеми квадратна хвиля пропускається через систему, яка затримує її вхід, яка застосовує лінійний фазовий зсув до спектру сигналу. Нехай затримка τ буде T/4. Скористайтеся передавальною функцією затримки для обчислення за допомогою Matlab рядів Фур'є вихідних даних. Покажіть, що квадратна хвиля дійсно затримується.

Наближення періодичних сигналів

Часто ми хочемо наблизити опорний сигнал дещо простішим сигналом. Для оцінки якості наближення найбільш часто використовуваною мірою похибки є середньоквадратична похибка. Для періодичного сигналу s (t),

$$\varepsilon ^{2}=\frac{1}{T}\int_{0}^{T}(s(t)-\overline{s}(t))^{2}dt \nonumber$$

де

$$s(t)=reference\; \; signal\\ \overline{s}(t)=approximation \nonumber$$

Одним із зручних способів знаходження наближень для періодичних сигналів є усічення їх рядів Фур'є.

$$\overline{s}(t)=\sum_{k=-K}^{K}c_{k}e^{i\frac{2\pi k}{T}t} \nonumber$$

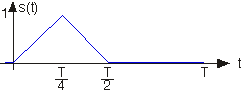
Суть цієї проблеми полягає в тому, щоб проаналізувати, чи є такий підхід найкращим (тобто завжди мінімізує середню квадратичну похибку). Знайдіть вираз частотної області для помилки наближення, коли ми використовуємо усічений ряд Фур'є як наближення. Замість того, щоб обрізати ряд, давайте узагальнимо характер наближення до включення будь-якого набору 2K+1 членів: Ми завжди будемо включати c ₀ і негативний індексований термін, що відповідає c _k. Який вибір термінів мінімізує середньоквадратичну похибку? Знайдіть вираз для помилки середнього квадрата, що виникає в результаті вашого вибору. Знайдіть ряд Фур'є для зображеного сигналу. Використовуйте Matlab для пошуку усіченого наближення та найкращого наближення за участю двох членів. Побудувати середню квадратичну похибку як функцію K для обох наближень.

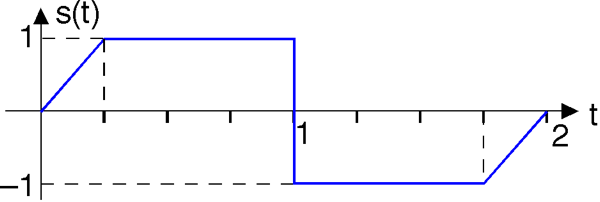
Довгі, спекотні дні

Добова температура є наслідком декількох ефектів, одним з них є сонячне нагрівання. Якби це було домінуючим ефектом, то добова температура була б пропорційна кількості світлового дня. Сюжет показує, що середньодобова висока температура поводиться не так.

У цій задачі ми хочемо зрозуміти температурну складову нашого середовища за допомогою ряду Фур'є та теорії лінійних систем. Файл temperature.mat містить ці дані (світловий день у першому рядку, відповідні середньодобові максимуми у другому) для Х'юстона, штат Техас. Нехай тривалість дня служить єдиним входом до системи, що має вихід, рівний середньодобовій температурі.

1. Вивчаючи графіки введення і виведення, ви б сказали, що система лінійна чи ні? Як ви дійшли висновку?
2. Знайдіть перші п'ять термінів (c ₀,... , c ₄) комплексного ряду Фур'є для кожного сигналу.
3. Що таке гармонійне спотворення в двох сигналах? Виключити c ₀ з цього розрахунку. Оскільки гармонійне спотворення невелике, давайте зосередимося тільки на першій гармоніці.
4. Що таке зсув фаз між вхідним і вихідним сигналами?
5. Знайдіть передавальну функцію найпростішої можливої лінійної моделі, яка б описувала дані.
6. Охарактеризувати і інтерпретувати структуру даної моделі. Зокрема, дайте фізичне пояснення фазового зсуву. Передбачте, яким буде вихід, якби модель не мала зсуву фаз. Чи були б дні спекотніше? Якщо так, то на скільки?

Пари перетворення Фур'є

Знайти Фур'є або обернене перетворення Фур'є наступного:

$$\forall :\left ( x(t)=e^{-(a\left | t \right |)} \right )x(t)=te^{-(at)}u(t)X(f)=\begin{cases} 1 & \text{ if } \left | f \right |< W \\ 0 & \text{ if } \left | f \right |> W \end{cases} \nonumber$$

$$x(t)=e^{-(at)}\cos (2\pi f_{0}t)u(t) \nonumber$$

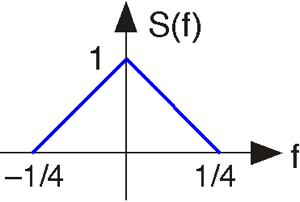
Подвійність у перетвореннях Фур'є

«Подвійність» означає, що перетворення Фур'є та зворотне перетворення Фур'є дуже схожі. Отже, форма хвилі s (t) у часовій області та спектр s (f) мають відповідно перетворення Фур'є та зворотне перетворення Фур'є, які дуже схожі.

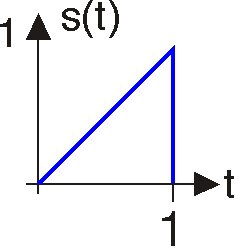
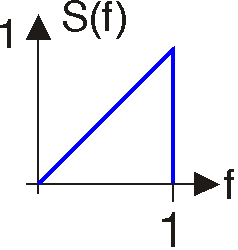
1. Обчисліть перетворення Фур'є сигналу, показаного вище.
2. Обчисліть зворотне перетворення Фур'є спектра, показаного вище.
3. Як пов'язані ці відповіді? Яка загальна залежність між перетворенням Фур'є s (t) та оберненим перетворенням s (f)?

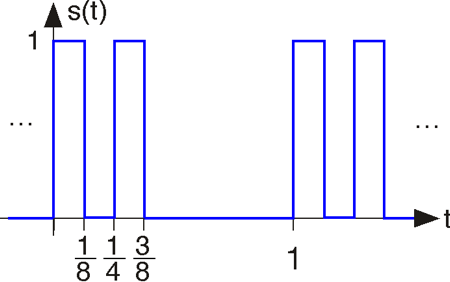
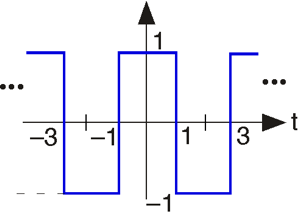
Спектри імпульсних послідовностей

Послідовності імпульсів часто трапляються в цифровому зв'язку та в інших сферах. Які їх спектральні властивості?

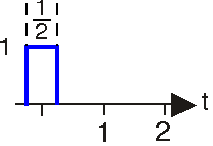
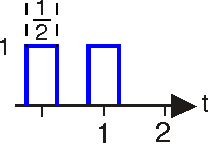
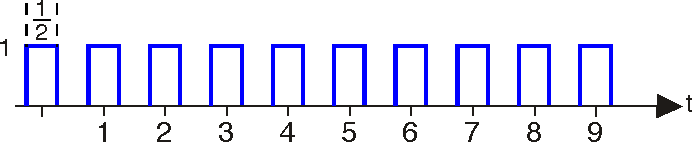
1. Обчисліть перетворення Фур'є одиночного імпульсу, показаного вище.
2. Обчисліть перетворення Фур'є двоімпульсної послідовності, наведеної вище.
3. Обчисліть перетворення Фур'є для десятиімпульсної послідовності, наведеної вище. Вам слід шукати загальний вираз, який містить послідовності будь-якої довжини.
4. Використовуючи Matlab, побудуйте величини трьох спектрів. Опишіть, як змінюються спектри при збільшенні кількості повторюваних імпульсів.

Спектри цифрових сигналів зв'язку

Один із способів представлення бітів сигналами показаний на малюнку нижче. Якщо значення біта дорівнює «1», воно представлено позитивним імпульсом тривалості T. Якщо це «0», він представлений негативним імпульсом тієї ж тривалості. Для представлення послідовності бітів належним чином підібрані імпульси розміщуються один за одним.

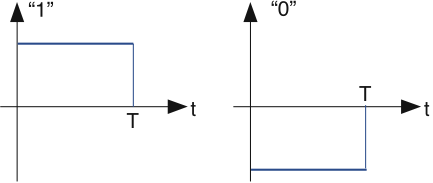
1. Який спектр форми хвилі представляє чергувану бітову послідовність «... 01010101...»?
2. Пропускна здатність цього сигналу визначається як діапазон частот, над яким міститься 90% потужності. Що таке пропускна здатність цього сигналу?
3. Припустимо, бітова послідовність стає «... 00110011...». Тепер що таке пропускна здатність?

Низькочастотна фільтрація квадратної хвилі

Нехай квадратна хвиля (період T) служить входом до системи нижніх частот першого порядку, побудованої як RC-фільтр. Ми хочемо отримати вираз для відповіді часової області фільтра на цей вхід. Спочатку розглянемо реакцію фільтра на простий імпульс, що має одиничну амплітуду і ширину T /2.

1. Вивести вираз для виведення фільтра до цього імпульсу. Відзначаючи, що квадратна хвиля є суперпозицією послідовності цих імпульсів, яка реакція фільтра на квадратну хвилю? Характер цієї реакції повинен змінюватися в міру зміни співвідношення між періодом квадратної хвилі та частотою зрізу фільтра.
2. Скільки часу повинен бути період, щоб відповідь не досягла відносно постійного значення між переходами в квадратній хвилі?
3. Яке відношення частоти зрізу фільтра до спектру квадратної хвилі в даному випадку?

Математика з схемами

Прості схеми можуть реалізовувати прості математичні операції, такі як інтеграція та диференціація. Ми хочемо розробити активну схему (вона містить операційний підсилювач), що має вихід, пропорційний інтегралу його входу. Наприклад, можна було використовувати інтегратор в автомобілі для визначення пройденої відстані від спідометра.

1. Що таке передавальна функція інтегратора?
2. Знайдіть схему операційного підсилювача так, щоб його вихідна напруга була пропорційною інтегралу його входу для всіх сигналів.

Звідки цей звук?

Ми визначаємо, звідки йде звук, тому що у нас два вуха і мозок. Звук рухається з відносно повільною швидкістю, і наш мозок використовує той факт, що звук буде надходити в одне вухо раніше за інше. Як показано нижче, звук, що виходить з правого, надходить на ліве вухо τ секунд після того, як він надходить у праве вухо.

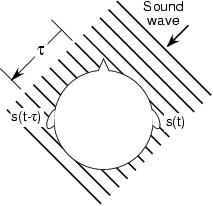
Як тільки мозок виявляє цю затримку поширення, він може визначити напрямок звуку. У спробі змоделювати те, що може зробити мозок, процесори сигналу RU хочуть розробити оптимальну систему, яка затримує сигнал кожного вуха на деяку кількість, а потім додає їх разом. Δ _l і Δ _r - затримки, застосовані до лівого і правого сигналів відповідно. Ідея полягає у визначенні значень затримки за деяким критерієм, який базується на тому, що вимірюється двома вухами.

1. Яка функція передачі між звуковим сигналом s (t) і виходом процесора y (t)? Одним із способів визначення затримки τ є вибір максимальної потужності в y (t).
2. Як ці затримки обробки максимальної потужності пов'язані з τ?

Домовленості систем

Архітектура системи модульних компонентів означає упорядкування їх у різних конфігураціях для досягнення деякого загального співвідношення вхід-виводу.

1. Для кожного з перерахованих нижче визначають загальну передавальну функцію між x (t) і y (t).

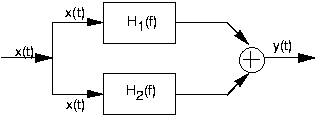
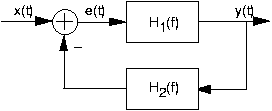
2. Загальна передавальна функція для каскаду (спочатку зображена система) особливо цікава. Що говорить про ефект впорядкування лінійних, інваріантних в часі систем в каскаді?

Фільтрація

Нехай сигнал

$$s(t)=\frac{\sin (\pi t)}{\pi t} \nonumber$$

бути входом до лінійного, інваріантного за часом фільтра, який має функцію передачі, показану нижче.

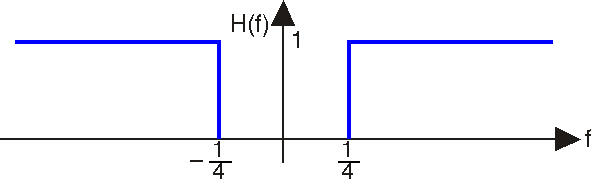
1. Знайдіть вираз для y (t), виведення фільтра.

Схеми фільтра

Входом в RC-ланцюг, що має передавальну функцію, служить одинично-амплітудний імпульс тривалістю однієї секунди.

$$H(f)=\frac{i2\pi f}{4+i2\pi f} \nonumber$$

1. Як би ви класифікували цю функцію передачі: низькочастотний, високочастотний, смуговий, інший?
2. Знайдіть схему, яка відповідає цій передавальної функції.
3. Знайдіть вираз для виводу фільтра.

Реверберація

Реверберація відповідає додаванню до сигналу його відкладеної версії.

1. Припускаючи, що τ являє собою затримку, яке відношення вхід-вихід для системи реверберації?
2. Чи є система лінійною та інваріантною за часом? Якщо так, знайдіть функцію передачі; якщо ні, то який критерій лінійності або часової інваріантності порушує реверберація.
3. Музична група, відома як RowLs, має проблеми з продажем своїх записів. Інженер звукозаписної компанії отримує ідею застосувати різну затримку до низьких і високих частот і додати результат для створення нового музичного ефекту. Таким чином, звук RowLs буде розділений на дві частини (одна менше частоти f ₀, інша більша за f ₀), вони будуть затримані на τ _l і τ _h відповідно, і додані отримані сигнали.
   1. Намалюйте блок-схему для цієї нової системи обробки звуку, показуючи її різні компоненти.
   2. Як залежить величина передавальної функції системи від двох затримок?

Відлуння в телефонних системах

Часто зустрічається проблема в телефонах - відлуння. Тут, через акустичну зв'язок між вушною частиною та мікрофоном у трубці, те, що ви чуєте, також надсилається людині, яка розмовляє. Ця людина, таким чином, не тільки чує вас, але і чує власну промову, затриману (через затримку поширення по телефонній мережі) і послаблюється (посилення акустичної зв'язку менше одиниці). Крім того, та ж проблема стосується і вас: акустична муфта виникає в її трубці, а також у вашій.

1. Розробити блок-схему, яка описує цю ситуацію.
2. Знайдіть функцію передачі між вашим голосом і тим, що чує слухач.
3. Кожен телефон містить систему зниження відлуння за допомогою електричних засобів. Яка проста система могла знулити відлуння?

Ефективна доставка наркотиків

У більшості пацієнтів потрібен час для того, щоб концентрація введеного препарату досягла постійного рівня в кровотоці. Як правило, якщо концентрація препарату у внутрішньовенній лінії пацієнта становить

$$C_{d}u(t) \nonumber$$

концентрація в кровотоці пацієнта становить

$$C_{p}(1-e^{-(at)})u(t) \nonumber$$

1. Припускаючи, що взаємозв'язок між концентрацією препарату в препараті пацієнта і поставленою концентрацією може бути описана як лінійна, інваріантна в часі система, що таке трансферна функція?
2. Іноді система доставки ліків йде шкереберть і доставляє наркотики з невеликим контролем. Якою була б концентрація препарату пацієнта, якби доставлена концентрація була пандусом? Точніше, якби це було $$C_{d}tu(t) \nonumber$$
3. Розумний лікар хоче мати гнучкість, щоб уповільнити або прискорити концентрацію препарату пацієнта. Іншими словами, концентрація повинна бути $$C_{p}(1-e^{-(bt)})u(t) \nonumber$$ з b більшою або меншою за a. Як слід змінити сигнал концентрації препарату, щоб досягти цього профілю концентрації?

Ловля Speeders з радаром

RU Electronics укладено контракт на розробку доплерівської радіолокаційної системи. Радіолокаційні передавачі випромінюють сигнал, який відскакує від будь-якого провідного об'єкта. Різниця сигналів між тим, що надсилається, та віддачею радіолокатора обробляється та витягнутими особливостями. У доплерівських системах швидкість об'єкта по напрямку радіолокаційного променя є особливістю, яку повинна витягти конструкція. Переданий сигнал є синусоїдою:

$$x(t)=A\cos (2\pi f_{c}t) \nonumber$$

Виміряний зворотний сигнал дорівнює

$$B\cos (2\pi ((f_{c}+\Delta f)t+\phi ) \nonumber$$

де частота зміщення доплера Δf дорівнює 10v, де v - швидкість автомобіля, що йде до передавача.

1. Спроектуйте систему, яка використовує передані та зворотні сигнали як входи та виробляє Δf.
2. Однією з проблем конструкцій, заснованих на надмірно спрощених цілях проектування, є те, що вони чутливі до немодельованих припущень. Як би ви змінили свій дизайн, якщо взагалі, щоб можна було визначити, чи йде автомобіль або до передавача?
3. Припустимо, два об'єкти, що рухаються з різною швидкістю, забезпечують повернення Як би ви змінили свій дизайн, якщо взагалі, щоб розмістити кілька повернень?

Демодуляція сигналу AM

Нехай m (t) позначають сигнал, який був амплітудно-модульований.

$$x(t)=A(1+m(t))\sin (2\pi f_{c}t) \nonumber$$

Радіостанції намагаються обмежити амплітуду сигналу m (t) так, щоб вона була менше одиниці за величиною. Частота f _c дуже велика в порівнянні з частотним змістом сигналу. Те, що нас турбує тут, - це не передача, а прийом. Так званий когерентний демодулятор просто множить сигнал x (t) на синусоїду, що має таку ж частоту, що і несуча і нижні частоти фільтрують результат.

1. Проаналізуйте цей приймач і покажіть, що він працює. Припустимо, що фільтр низьких частот ідеально підходить. Однією з питань когерентного прийому є фаза синусоїди, яка використовується приймачем щодо тієї, що використовується передавачем.
2. Припускаючи, що синусоїда приймача має фазу φ , як залежить вихід від φ ?
3. Яке найгірше можливе значення для цієї фази?
4. Некогерентний приймач частіше використовується через проблему чутливості фази, властивої когерентному прийому. Тут приймач повнохвильовий випрямляє прийнятий сигнал і низькочастотний фільтрує результат (знову ж таки в ідеалі). Проаналізуйте цей приймач. Чи відрізняється його вихід від виходу когерентного приймача значним чином?

Незвичайна амплітудна

Ми хочемо надіслати обмежений смугою сигнал, що має зображений сигнал з амплітудною модуляцією звичайним способом. I.B. Різні пропонує використовувати носій квадратної хвилі, показаний нижче. Ну, це інакше, але його друзі задаються питанням, чи може якась техніка демодулювати її.

1. Знайти вираз для X (f), перетворення Фур'є модульованого сигналу.
2. Намалюйте величину X (f) , обережно позначаючи важливі величини та частоти.
3. Яка методика демодуляції, очевидно, працює?
4. I.B. кидає виклик трьом своїм друзям демодулювати x (t) іншим способом. Один друг пропонує модулювати x (t) з cos (πt/2), інший хоче спробувати модулювати cos (πt), а третій вважає, що cos (3πt/2) буде працювати.
   1. Намалюйте величину перетворення Фур'є сигналу, який виробляє підхід кожного учня.
   2. Який студент наближається до відновлення вихідного сигналу? Чому?

Семмі засинає...

Сидячи в класі ELEC 241, він засинає під час критичного часу, коли описується приймач AM. Отриманий сигнал має вигляд:

$$r(t)=A(1+m(t))\cos (2\pi f_{c}t+\varphi ) \nonumber$$

де фаза φ невідома. Сигнал повідомлення - m (t); він має пропускну здатність W Гц і величину менше 1 (|m (t) | <1). Фаза φ невідома. Інструктор намалював схему для приймача на дошці; Семмі проспав опис того, що невідомі системи де.

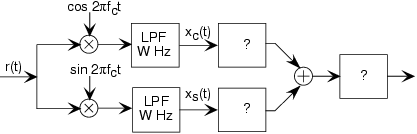
1. Які бувають сигнали x _c (t) і x _s (t)?
2. Що б ви поставили для невідомих систем, які гарантували б, що кінцевий вихід містив повідомлення незалежно від фази?
3. Семмі, можливо, спав, але він може придумати набагато простіший приймач. Що це таке?

заклинювання

Коледж Сіда Річардсона вирішує створити власну радіостанцію AM KSRR. Резидент-електрик вирішує, що вона може вибрати будь-яку несучу частоту і пропускну здатність повідомлення для станції. Конкурентний коледж вирішує заглушити свої передачі, передаючи сигнал високої потужності, який заважає радіостанціям, які намагаються отримати KSRR. Застрягання сигналу заклинювання (t) - це те, що відоме як пилкоподібна хвиля (як показано нижче), що має період, відомий інженеру KSRR.

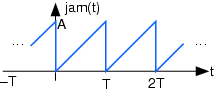
1. Знайдіть спектр сигналу глушіння.
2. Чи може KSRR повністю обійти спробу заклинити його, ретельно вибираючи несучу частоту та пропускну здатність передачі? Якщо так, знайдіть несучу частоту станції та пропускну здатність передачі з точки зору T, періоду сигналу перешкод; якщо ні, покажіть, чому б ні.

AM стерео

Стереофонічний сигнал складається з «лівого» сигналу l (t) та «правого» сигналу r (t), який передає звуки, що надходять з лівої та правої сторін оркестру відповідно. Для передачі цих двох сигналів одночасно передавач спочатку формує сигнал суми:

$$s_{+}(t)=l(t)+r(t) \nonumber$$

і різницевий сигнал

$$s_{-}(t)=l(t)-r(t) \nonumber$$

Потім амплітуда-передавач модулює різницевий сигнал синусоїдою, що має частоту 2W, де W - пропускна здатність лівого і правого сигналів. Сума сигналу і модульований різницевий сигнал додаються, сума амплітудно-модульована до несучої частоти радіостанції f _c, і передається. Припустимо, що спектри лівого та правого сигналів, як показано на малюнку.

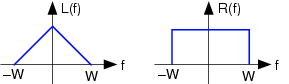
1. Що таке вираз для переданого сигналу? Намалюйте його спектр.
2. Покажіть блок-схему стерео приймача AM, який може давати лівий і правий сигнали як окремі виходи.
3. Який сигнал буде вироблятися звичайним когерентним приймачем AM, який очікує отримати стандартний сигнал AM, що передає сигнал повідомлення, що має пропускну здатність W?

Новий стерео метод AM

Розумний інженер подав патент на новий метод передачі двох сигналів одночасно в тій же смузі пропускання, що і комерційне AM радіо. Як показано нижче, її підхід полягає в модуляції позитивної частини носія одним сигналом, а негативної - другим.

Детально два сигнали повідомлень m ₁ (t) і m ₂ (t) обмежені частотою W Гц і мають максимальні амплітуди, рівні 1. Носій має частоту f _c набагато більше, ніж W. Переданий сигнал x (t) задається:

$$x(t)=\begin{cases} A(1+am_{1}(t))\sin (2\pi f_{c}t) & \text{ if } \sin (2\pi f_{c}t)\geq 0 \\ A(1+am_{2}(t))\sin (2\pi f_{c}t) & \text{ if } \sin (2\pi f_{c}t)< 0 \end{cases} \nonumber$$

У всіх випадках 0<a<1. Сюжет показує переданий сигнал, коли повідомлення є синусоїдами:

$$m_{1}(t)=\sin (2\pi f_{m}t)\; and\;\; m_{2}(t)=\sin (2\pi f_{m}t) \nonumber$$

де 2f _m < W.

1. Ви, як патентний експерт, повинні визначити, чи відповідає схема його претензіям і є корисною. Надайте більш стислий вираз для переданого сигналу x (t), ніж наведено вище.
2. Що таке ресивер за цією схемою? Це дасть як m ₁ (t), так і m ₂ (t) від x (t) .
3. Знайти спектр позитивної частини переданого сигналу. Визначити, чи відповідає ця схема критеріям проектування, що дозволяє видавати патент. Поясніть свої міркування.

Радикальна ідея радіо

Студент ELEC 241 має яскраву ідею використовувати квадратну хвилю замість синусоїди як носій AM. Переданий сигнал мав би вигляд:

$$x(t)=A(1+am(t))sq_{T}(t) \nonumber$$

де сигнал повідомлення m (t) буде обмеженим амплітудою: |m (t) |<1

1. Припускаючи, що сигнал повідомлення є низькочастотним і має пропускну здатність W Гц, які значення для періоду квадратної хвилі T можливі. Іншими словами, чи перешкоджають прийому деякі комбінації W і T?
2. Припускаючи, що прийом можливий, чи можуть стандартні радіостанції отримувати цю інноваційну передачу AM? Якщо так, покажіть, як когерентний приймач може демодулювати його; якщо ні, покажіть, як буде пошкоджений вихід когерентного приймача. Припустимо, що пропускна здатність повідомлення W=5 кГц.

Таємне спілкування

Амплітудно-модульоване секретне повідомлення m (t) має наступний вигляд:

$$r(t)=A(1+am(t))\cos (2\pi (f_{c}+f_{0})t) \nonumber$$

Сигнал повідомлення має пропускну здатність W Гц і величину менше 1 (|m (t) | <1). Ідея полягає в зміщенні несучої частоти на f ₀ Гц від стандартних частот радіоносія. Таким чином, «поза полицею» когерентні демодулятори припускають, що несуча частота має f _c Гц. Тут, f ₀ < Вт

1. Намалюйте спектр демодульованого сигналу, виробленого когерентним демодулятором, налаштованим на f _c Гц.
2. Чи буде цей демодульований сигнал «скрембльованою» версією оригіналу? Якщо так, то як так; якщо ні, то чому б і ні?
3. Чи можете ви розробити приймач, який може демодулювати повідомлення, не знаючи частоти зсуву f _c?

Скремблювання сигналу

Схвильований винахідник оголошує про відкриття способу використання аналогової технології, щоб зробити музику непрослухованою, не знаючи секретного методу відновлення. Ідея полягає в тому, щоб модулювати обмежений смугою повідомлення m (t) спеціальним періодичним сигналом s (t), який дорівнює нулю протягом половини його періоду, що робить повідомлення непрослухованим і поверхнево, принаймні, невідновним (див. Малюнок нижче).

1. Що таке ряд Фур'є для періодичного сигналу?
2. Які обмеження на період Т, щоб сигнал повідомлення можна було відновити з m (t) s (t)?
3. Студенти ELEC 241 вважають, що вони «зламали» схему винахідника і збираються оголосити її світові. Як би вони відновили вихідне повідомлення, не маючи детальних знань про модулюючий сигнал?