4.7: Фільтрація періодичних сигналів

Цілі навчання

• Цей модуль демонструє вплив, який інваріантний фільтр може мати на періодичні сигнали.

Подання періодичного сигналу рядів Фур'є дозволяє легко визначити, як лінійний інваріантний фільтр змінює такі сигнали загалом. Фундаментальна властивість лінійної системи полягає в тому, що її співвідношення вхід-вихід підпорядковується суперпозиції:

$$L\left ( a_{1}s_{1}(t)+a_{2}s_{2}(t) \right )=a_{1}L\left ( s_{1}(t) \right )+a_{2}L\left ( s_{2}(t) \right ) \nonumber$$

Оскільки ряд Фур'є представляє періодичний сигнал як лінійну комбінацію складних експоненціальних, ми можемо використовувати властивість суперпозиції. Крім того, ми виявили для лінійних ланцюгів, що їх вихід на складний експоненціальний вхід - це лише частотна характеристика, оцінена на частоті сигналу раз складної експоненціальної. Сказано математично, якщо:

$$x(t)=e^{i\frac{2\pi kt}{T}} \nonumber$$

потім вихід

$$y(t)=H\left ( \frac{k}{T} \right )e^{i\frac{2\pi kt}{T}} \nonumber$$

оскільки

$$f= \frac{k}{T} \nonumber$$

Таким чином, якщо x (t) є періодичним, тим самим маючи ряд Фур'є, вихід лінійної схеми на цей сигнал буде суперпозицією виходу до кожного компонента.

$$y(t)=\sum_{k=-\infty }^{\infty }c_{k}H\left ( \frac{k}{T} \right )e^{i\frac{2\pi kt}{T}} \nonumber$$

Таким чином, на виході є ряд Фур'є, а значить, він теж періодичний. Його коефіцієнти Фур'є дорівнюють:

$$c_{k}H\left ( \frac{k}{T} \right ) \nonumber$$

Для отримання спектра виходу просто множимо вхідний спектр на частотну характеристику. Схема змінює величину і фазу кожного коефіцієнта Фур'є. Зверніть увагу, особливо, що, хоча коефіцієнти Фур'є не залежать від періоду сигналу, функція передачі ланцюга залежить від частоти, а це означає, що вихід схеми буде відрізнятися в міру зміни періоду.

Малюнок 4.7.1a Періодичний імпульсний сигнал

Малюнок 4.7.1b Верхні графіки показують спектр імпульсного сигналу для різних частот зрізу. Нижні графіки показують вихідні сигнали фільтра.

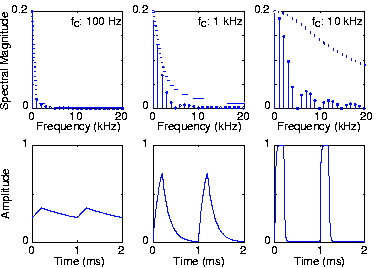
На наведеному вище малюнку 4.7.1b періодичний імпульсний сигнал, такий як показано на лівій частині, де (Δ/2 = 0,2), служить входом для RC фільтра низьких частот. Період введення становив 1 мс (мілісекунди). Частота зрізу фільтра була встановлена на різні значення, зазначені у верхньому рядку, які відображають спектр вихідного сигналу та функцію передачі фільтра. У нижньому рядку показаний вихідний сигнал, отриманий з коефіцієнтів рядів Фур'є, показаних у верхньому рядку.

Приклад$\PageIndex{1}$:

Періодичний імпульсний сигнал, показаний зліва вище, служить входом в RC-ланцюг, який має передавальну функцію

$$H(f)=\frac{1}{1+i2\pi fRC} \nonumber$$

На малюнку 4.7.1b показані зміни на виході, коли ми змінюємо частоту зрізу фільтра. Зверніть увагу, як спектр сигналу поширюється набагато вище його основної частоти. Маючи частоту зрізу в десять разів вище, ніж фундаментальна, помітно змінює вихідну форму хвилі, округляючи провідні та задні краї. Коли частота зрізу зменшується (центр, потім ліворуч), округлення стає більш помітним, а крайня ліва форма хвилі показує невелику пульсацію.

Вправа$\PageIndex{1}$

Яке середнє значення кожної вихідної форми сигналу? Правильна відповідь може вас здивувати.

Рішення

Оскільки коефіцієнт посилення фільтра на нульовій частоті дорівнює одиниці, середні вихідні значення дорівнюють відповідним середнім вхідним значенням.

Цей приклад також ілюструє вплив фільтра низьких частот на форму хвилі. Простий RC-фільтр, який використовується тут, має досить поступову частотну характеристику, а це означає, що вищі гармоніки плавно придушуються. Пізніше ми опишемо фільтри, які мають набагато швидше змінюються частотні характеристики, що дозволяє набагато більш драматично вибрати вхідні коефіцієнти Фур'є.

Що ще важливіше, ми розрахували вихід схеми на періодичний вхід без запису, а тим більше рішення диференціального рівняння, що регулює поведінку схеми. Крім того, ми зробили ці розрахунки повністю в частотній області. Використовуючи ряди Фур'є, ми можемо обчислити, як будь-яка лінійна схема буде реагувати на періодичний вхід.