4.5: Наближення сигналів рядів Фур'є

Last updated
Save as PDF

Page ID: 32758

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

Наближення рядів Фур'є.

Цікаво розглянути послідовність сигналів, яку ми отримуємо при включенні більшої кількості членів у наближення рядів Фур'є напівхвильової випрямленої синусоїди. Визначте s _K (t) як сигнал, що містить умови К+1 Фур'є.

\[s_{K}(t)=a_{0}+\sum_{k=1}^{K}a_{k}\cos \left ( \frac{2\pi kt}{T} \right )+ \sum_{k=1}^{K}b_{k}\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]

На малюнку 4.5.1 нижче показано, як ця послідовність сигналів зображує сигнал більш точно, оскільки додається більше термінів.

Малюнок 4.5.1 У верхній частині показаний спектр ряду Фур'є напівхвильової випрямленої синусоїди.

Індекс вказує кратну основній частоті, на якій сигнал має енергію. У нижній частині показано кумулятивний ефект додавання термінів до ряду Фур'є для напівхвильової випрямленої синусоїди. Пунктирна лінія є фактичним сигналом, при цьому суцільна лінія показує наближення скінченного ряду до зазначеної кількості членів, K+1.

Нам потрібно кількісно оцінити точність наближення рядів Фур'є, щоб ми могли судити про те, наскільки швидко ряд наближається до сигналу. Коли ми використовуємо

\[\varepsilon _{K}(t)=\sum_{k=K+1}^{\infty }a_{k}\cos \left ( \frac{2\pi kt}{T} \right )+ \sum_{k=K+1}^{\infty }b_{k}\sin \left ( \frac{2\pi kt}{T} \right ) \nonumber \]

Щоб знайти помилку rms, ми повинні квадратувати цей вираз та інтегрувати його протягом певного періоду. Знову ж таки, інтеграл більшості перехресних членів дорівнює нулю, залишаючи

\[rms(\varepsilon _{K})=\sqrt{\frac{1}{2}\sum_{k=K+1}^{\infty }a_{k}^{2}+b_{k}^{2}} \nonumber \]

На малюнку 4.5.2 показано, як зменшується похибка в рядах Фур'є для напівхвильової випрямленої синусоїди з урахуванням більшої кількості членів. Зокрема, використання чотирьох термінів, як показано на нижньому графіку малюнка 4.5.1, має середньоквадратичну похибку (щодо середньоквадратичного значення сигналу) близько 3%. Ряд Фур'є в цьому випадку швидко сходиться до сигналу.

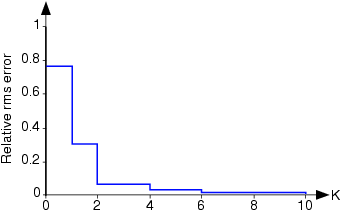
Малюнок 4.5.2 Похибка наближення для напівхвильової випрямленої синусоїди

Середньоквапльова похибка, розрахована відповідно до наведеного вище рівняння, показана як функція кількості членів у ряді для напівхвильової випрямленої синусоїди. Помилка була нормована середньоквадратичним значенням сигналу.

Ми можемо подивитися на рис. 4.5.3, щоб побачити спектр потужності та середньоквадратичну похибку наближення для квадратної хвилі.

Малюнок 4.5.3 Верхній графік показує спектр потужності квадратної хвилі, а на нижньому - середньоквадратичну похибку наближення рядів Фур'є скінченної довжини до квадратної хвилі. Зірочка позначає середньоквадратичну похибку, коли кількість членів K в ряді Фур'є дорівнює 99.

Оскільки коефіцієнти Фур'є падають тут повільніше, ніж для напівхвильової випрямленої синусоїди, середньоквадратична похибка не зменшується швидко. Іншим способом, спектр квадратної хвилі містить більше потужності на більш високих частотах, ніж напівхвильова випрямлена синусоїда. Ця різниця між двома рядами Фур'є призводить до того, що коефіцієнти Фур'є напівхвильової випрямленої синусоїди пропорційні 1/k ², тоді як коефіцієнти квадратної хвилі пропорційні 1/k. Насправді, після 99 членів наближення квадратної хвилі похибка більша за 10 членів наближення для напівхвильової випрямленої синусоїди. Математики показали, що жоден сигнал не має середньоквадратичної помилки наближення, яка розпадається повільніше, ніж для квадратної хвилі.

Вправа\(\PageIndex{1}\)

Обчисліть гармонійне спотворення для квадратної хвилі.

Рішення

Сумарне гармонійне спотворення в квадратній хвилі становить:

\[1-\frac{1}{2}(\frac{4}{\pi })^{2}=20\% \nonumber \]

Більше, ніж просто повільно розкладається, наближення рядів Фур'є, показане на малюнку 4.5.4, демонструє цікаву поведінку.

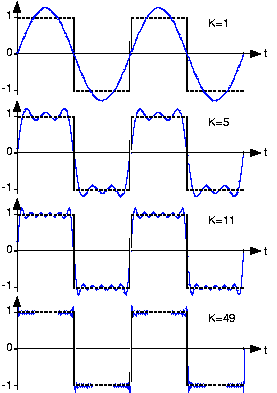
Малюнок 4.5.4 Наближення рядів Фур'є до **sq (t).** Кількість членів у сумі Фур'є вказується на кожному графіку, а квадратна хвиля відображається пунктирною лінією протягом двох періодів.

Хоча ряд Фур'є квадратної хвилі вимагає більше термінів для заданої точності подання, при порівнянні графіків не ясно, що ці два рівні. Чи дійсно ряд Фур'є дорівнює квадратній хвилі при всіх значеннях

Розглянемо це математичне питання інтуїтивно: чи може переривчаста функція, як квадратна хвиля, бути виражена як сума, навіть нескінченна, безперервних сигналів? Треба хоча б бути підозрілим, і насправді, це не може бути таким вираженим. Це питання викликало Фур'є багато критики з боку Французької академії наук (Лаплас, Лагранж, Монж і Лакруа складали комітет з огляду) протягом декількох років після його презентації 1807 року. Вона не вирішувалася майже століття, і її дозвіл цікаво і важливо розуміти з практичної точки зору.

Сторонні піки в серії Фур'є квадратної хвилі ніколи не зникають; вони називаються явищем Гібба після американського фізика Джосії Віллард Гіббс. Вони виникають всякий раз, коли сигнал переривається, і завжди будуть присутніми, коли сигнал має стрибки.

Повернемося до питання рівності; як може бути виправданий знак рівності у визначенні ряду Фур'є? Часткова відповідь полягає в тому, що точково —кожне значення t —рівність не гарантується. Однак математики пізніше в дев'ятнадцятому столітті показали, що середньоквадратична похибка ряду Фур'є завжди дорівнювала нулю.

\[\lim_{k \to\infty }rms(\varepsilon _{K})=0 \nonumber \]

Це означає, що помилка між сигналом та його наближенням ряду Фур'є може бути не нулем, але що його середньоквадратичне значення буде нульовим! Саме очима значення rms ми перевизначаємо рівність: Звичайне визначення рівності називається точковою рівністю: Два сигнали s ₁ (t), s ₂ (t) вважаються рівними точково, якщо:

\[s_{1}(t)=s_{2}(t) \nonumber \]

для всіх значень t. Нове визначення рівності - середньоквадратична рівність: Два сигнали вважаються рівними в середньому квадраті, якщо:

\[rms(s_{1}-s_{2})=0 \nonumber \]

Для рядів Фур'є піки явища Гібба мають кінцеву висоту і нульову ширину. Помилка відрізняється від нуля лише в ізольованих точках - всякий раз, коли періодичний сигнал містить розриви - і дорівнює приблизно 9% від розміру розриву. Значення функції на скінченній множині точок не впливає на її інтеграл. Цей ефект лежить в основі причини, чому визначення значення розривної функції, як ми утрималися від визначення ступінчастої функції, при її розриві є безглуздим. Що б ви не вибрали для значення, не має практичного значення ні для спектру сигналу, ні для того, як система реагує на сигнал. Значення ряду Фур'є «при» розриві є середнім значенням значень по обидва боки стрибка.