3.19: Операційні підсилювачі
- Page ID
- 33216
- Короткий опис роботи операційного підсилювача.
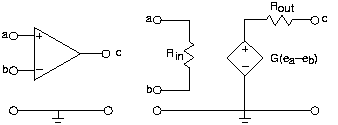
OP-підсилювачі мають не тільки модель схеми, показану на малюнку 3.19.1 вище, але їх значення елементів дуже особливі.
- Вхідний опір, R in, зазвичай великий, порядку 1 МОм.
- Вихідний опір, R out, невеликий, зазвичай менше 100 Ом.
- Коефіцієнт посилення напруги, G, великий, перевищує 10 5.
Великий коефіцієнт посилення кидається в очі; це говорить про те, що операційний підсилювач може перетворити вхідний сигнал 1 мВ на 100 В. Якби ви будували таку схему - приєднуючи джерело напруги до вузла a, приєднуючи вузол b до еталонного та дивлячись на вихід - ви б розчарувалися. Маючи справу з електронними компонентами, ви не можете забути про непредставленому, але необхідному блоці живлення.
Електронні компоненти не можуть видавати напруги, що перевищують передбачені джерелом живлення або для них видавати струми, що перевищують номінальний показник джерела живлення.
Типові напруги живлення, необхідні для схем операційних підсилювачів, складають + (15 В). Приєднання сигналу 1 mv не тільки не зможе створити сигнал 100 В, результуюча форма хвилі буде сильно спотворена. Хоча бажаний результат, якщо ви любитель рок-н-ролу, високоякісні стереосистеми не повинні спотворювати сигнали. Іншим міркуванням при розробці схем з операційним підсилювачем є те, що ці значення елементів є типовими: Ретельний контроль посилення можна отримати лише шляхом вибору схеми, щоб значення її елементів диктували результуючий коефіцієнт посилення, який повинен бути меншим, ніж той, що забезпечується операційним підсилювачем.
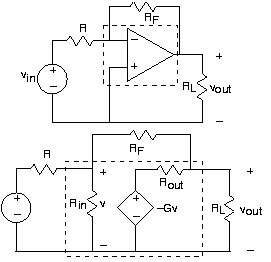
Інвертуючий підсилювач
Конфігурація зворотного зв'язку, показана на малюнку 3.19.2, є найпоширенішою схемою операційного підсилювача для отримання того, що відомо як інвертуючий підсилювач.
\[\left ( \frac{R_{F}R_{out}}{R_{out}-GR_{F}}\left ( \frac{1}{R_{out}}+\frac{1}{R_{in}}+\frac{1}{R_{L}}\right )\left ( \frac{1}{R}+\frac{1}{R_{in}}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
забезпечує точне співвідношення вхід-виводу. Вибираючи значення елементів щодо характеристик операційного підсилювача, ми можемо значно спростити вираз.
- Зробіть опір навантаження, R L, набагато більше R out. Ця ситуація скидає термін 1/R L з другого множника вищевказаного рівняння.
- Зробіть резистор, R, менше R в, що означає, що 1/R в терміні в третьому коефіцієнті мізерно малий.
З цими двома критеріями проектування виразом стає:
\[\left ( \frac{R_{F}R_{out}}{R_{out}-GR_{F}}\left ( \frac{1}{R}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
Оскільки коефіцієнт посилення великий, а опір R out малий, перший член стає -1/G, залишаючи нас з:
\[\left ( \left ( -\frac{1}{G} \right )\left ( \frac{1}{R}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]
Якщо ми виберемо значення R F і R так, що GR>>R F, цей коефіцієнт більше не буде залежати від властивого підсилювача коефіцієнта посилення, і він дорівнюватиме -1/R F. За цих умов ми отримуємо класичне співвідношення вхід-вихід для інвертуючого підсилювача на основі операційного підсилювача.
\[v_{out}=-\left ( \frac{R_{F}}{R}v_{in} \right ) \nonumber \]
Отже, коефіцієнт посилення, що надається нашою схемою, цілком визначається нашим вибором резистора зворотного зв'язку R F і вхідного резистора R. Він завжди негативний, і може бути менше одиниці або більше одиниці за величиною. Він не може перевищувати властивий операційний підсилювач коефіцієнт посилення і не повинен виробляти такі великі виходи, що призводить до спотворення (пам'ятайте про джерело живлення!). Цікаво, зауважте, що це співвідношення не залежить від опору навантаження. Цей ефект виникає тому, що ми використовуємо опори навантаження великі порівняно з вихідним опором операційного підсилювача. Таким чином, спостереження означає, що, якщо обережно, ми можемо розмістити схеми операційних підсилювачів у каскад, не викликаючи ефекту наступних схем, що змінюють поведінку (передавальну функцію) попередніх; побачити цю проблему.
Активні фільтри
Поки виконуються вимоги до конструкції, співвідношення вхід-вихід для інвертуючого підсилювача також застосовується, коли елементи зворотного зв'язку та вхідного ланцюга є імпедансами (резистори, конденсатори та індуктори).
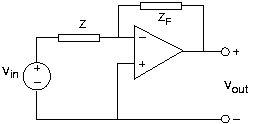
\[\frac{V_{out}}{V_{in}}=-\frac{Z_{F}}{Z} \nonumber \]
Давайте спроектуємо схему операційного підсилювача, яка функціонує як фільтр низьких частот. Ми хочемо, щоб функція передачі між вихідною та вхідною напругою була:
\[H(f)=\frac{K}{1+\frac{if}{f_{c}}} \nonumber \]
де K дорівнює коефіцієнту посилення смуги пропускання, а f c - частота зрізу. Припустимо, що інверсія (негативне посилення) значення не має. Маючи на увазі функцію передачі вищевказаної схеми операційного підсилювача, давайте розглянемо деякі варіанти.
- \[Z_{F}=K,\; \; Z=1+\frac{if}{f_{c}} \nonumber \]
Цей вибір означає, що імпеданс зворотного зв'язку є резистором і що вхідний опір являє собою послідовну комбінацію індуктора і резистора. У схемному дизайні ми намагаємося уникати індукторів, оскільки вони фізично громіздкіші, ніж конденсатори.
- \[Z_{F}=\frac{1}{1+\frac{if}{f_{c}}},\; \; Z=\frac{1}{K} \nonumber \]
Розглянемо зворотний імпеданс зворотного зв'язку (його допустимість):
\[Z_{F}^{-1}=1+\frac{if}{f_{c}} \nonumber \]
Оскільки цей допуск є сумою допусків, цей вираз передбачає паралельне поєднання резистора (значення = 1 Ом) і конденсатора (значення = (1/f c) F). У нас є правильна ідея, але значення (як 1 Ом) не мають рації. Розглянемо загальну паралельну комбінацію RC; її допуск є
\[\frac{1}{R_{F}}+i2\pi fC \nonumber \]
Допускаючи вхідний опір дорівнює R, передавальна функція підсилювача, що інвертує підсилювач, тепер
\[H(f)=-\frac{\frac{R_{F}}{R}}{1+i2\pi fR_{F}C} \nonumber \]
де виграш дорівнює
\[\frac{R_{F}}{R} \nonumber \]
і частота зрізу
\[\frac{1}{R_{F}C} \nonumber \]
Створення певної функції передачі за допомогою op-підсилювачів не має унікальної відповіді. На відміну від конструкції з пасивними схемами, електроніка є більш гнучкою (каскад схем може бути побудований так, що кожен мало впливає на інші; див. [посилання]) і посилення (збільшення потужності та амплітуди) може призвести. Щоб завершити наш приклад, припустимо, що ми хочемо фільтр низьких частот, який імітує те, що роблять телефонні компанії. Сигнали, що передаються по телефону, мають верхню межу частоти близько 3 кГц. Для другого вибору дизайну нам потрібно R F C = 5.3x10 -5. Таким чином, багато варіантів для значень опору та ємності можливі. Конденсатор 1 мкФ і резистор 330 Ом, 10 нФ і 33 кОм, і 10 пФ і 33 МОм все теоретично працювали б. Давайте також бажаємо посилення напруги в десять:
\[\frac{R_{F}}{R}=10 \nonumber \]
\[R=\frac{R_{F}}{10} \nonumber \]
Нагадаємо, що ми повинні мати R <R в.
Оскільки вхідний опір операційного підсилювача становить близько 1 МОм, ми не хочемо
\[\frac{\left | Z_{F} \right |}{R}< 10^{5} \nonumber \]
для всіх частот, що цікавлять. Таким чином,
\[\frac{\frac{R_{F}}{\left | 1+i2\pi fR_{F}C \right |}}{R}< 10^{5} \nonumber \]
Оскільки цей імпеданс зменшується з частотою, специфікація конструкції
\[\frac{R_{F}}{R}=10 \nonumber \]
означає, що цей критерій легко дотриматися. Таким чином, перші два варіанти для значень резистора і конденсатора (як і багато інших в цьому діапазоні) будуть працювати добре. Додаткові міркування, такі як вартість деталей, можуть увійти в картину. Якщо у вас немає потужного додатка (це не одне) або не попросіть високоточні компоненти, витрати не сильно залежать від значень компонентів, поки ви залишаєтеся близько до стандартних значень. Для резисторів, що мають значення r10 d, легко отримані значення
Що особливого щодо значень резистора; чому ці досить непарні значення для r?
Рішення
Співвідношення між сусідніми значеннями приблизно\[\sqrt{2} \nonumber \]
Інтуїтивний спосіб вирішення схем операційних підсилювачів
Коли ми зустрічаємо специфікації конструкції операційного підсилювача, ми можемо значно спростити наші розрахунки схем, настільки, що нам не потрібна модель схеми операційного підсилювача для визначення функції передачі. Ось наш інвертуючий підсилювач.
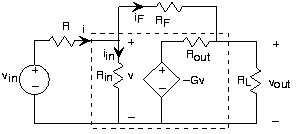
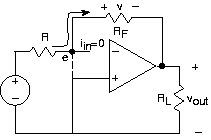
Коли ми скористаємося характеристиками операційного підсилювача - великим вхідним опором, великим коефіцієнтом посилення та малим вихідним опором - ми відзначаємо два наступні важливі факти.
- Струм i в повинен бути дуже маленьким. Напруга, що виробляється залежним джерелом, в 10 5 разів перевищує напругу v. Таким чином, напруга
- Через це припущення - по суті немає потоку струму через R в - напрузі
Озброївшись цими наближеннями, повернемося до нашої початкової схеми, як показано на малюнку 3.19.4. Напруга вузла е по суті дорівнює нулю, тобто воно по суті прив'язане до опорного вузла. Таким чином, струм через резистор R дорівнює:
\[i=\frac{v_{in}}{R} \nonumber \]
Крім того, резистор зворотного зв'язку з'являється паралельно з навантажувальним резистором. Оскільки струм, що йде в операційний підсилювач, дорівнює нулю, весь струм, що протікає через R, протікає через резистор зворотного зв'язку (i F = i)! Напруга на резисторі зворотного зв'язку R дорівнює:
\[v=\frac{v_{in}R_{F}}{R} \nonumber \]
Оскільки лівий кінець резистора зворотного зв'язку по суті прикріплений до опорного вузла, напруга на ньому дорівнює негативному тому, що на вихідному резисторі:
\[v_{out}=-v=-\frac{v_{in}R_{F}}{R} \nonumber \]
Використання такого підходу значно полегшує аналіз нових схем операційних підсилювачів. Використовуючи цю техніку, перевірте, чи отримані результати відповідають припущенням, що по суті нульовий струм надходить в операційний підсилювач і майже нульова напруга на входах операційного підсилювача.
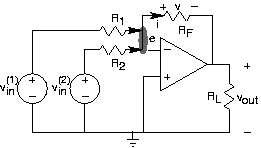
Спробуємо цю методику аналізу на простому розширенні конфігурації інвертуючого підсилювача, показаної на наведеному вище малюнку 3.19.5. Якщо жодної з комбінацій джерело-резистор не було, інвертуючий підсилювач залишається, і ми знаємо, що передавальна функція. За суперпозицією ми знаємо, що відношення входу-виводу є:
\[v_{out}=\left ( -\left ( \frac{R_{F}}{R_{1}} v_{in}^{(1)}\right ) \right )-\frac{R_{F}}{R_{2}} v_{in}^{(2)} \nonumber \]
Коли ми починаємо з нуля, вузол, що з'єднує три резистори, має той же потенціал, що і еталонний,
\[e\simeq 0 \nonumber \]
Сума струмів, що протікають в цей вузол, дорівнює нулю. Таким чином, струм i, що протікає в резисторі R F, дорівнює:
\[i=\frac{v_{in}^{(1)}}{R_{1}}+\frac{v_{in}^{(2)}}{R_{2}} \nonumber \]
Оскільки резистор зворотного зв'язку по суті паралельний навантажувальному резистору, напруги повинні задовольняти
\[v=-v_{out} \nonumber \]
Таким чином ми отримуємо наведене вище відношення «вхід-вихід».
Яку утиліту має ця схема? Чи можна розширити основне поняття схеми без обмежень?
