3.18: Залежні джерела

Цілі навчання

• Залежні джерела.

Залежне джерело

Залежним джерелом є або джерело напруги, або струму, значення якого пропорційно деякому іншому напрузі або струму в ланцюзі.

Таким чином, існує чотири різних види залежних джерел; для опису операційного підсилювача нам потрібен джерело напруги, залежне від напруги. Однак стандартна схемо-теоретична модель для транзистора містить струмозалежне джерело струму. Залежні джерела не служать входами в ланцюг, як незалежні джерела. Вони використовуються для моделювання активних схем: тих, що містять електронні елементи. Схеми RLC, які ми розглядали до цих пір, відомі як пасивні схеми.

Малюнок 3.18.1 З чотирьох можливих залежних джерел зображено джерело напруги, залежне від напруги в контексті загальної схеми.

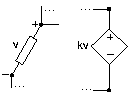
Операційний підсилювач

На малюнку 3.18.2 нижче показаний символ схеми операційного підсилювача і його еквівалентна ланцюг з точки зору джерела напруги, залежного від напруги.

Малюнок 3.18.2 Операційний підсилювач має чотири клеми, до яких можуть бути зроблені з'єднання. Входи приєднуються до вузлів a і b, а вихід - вузол c. Як показує модель схеми праворуч, операційний підсилювач служить підсилювачем різниці напруг вхідного вузла.

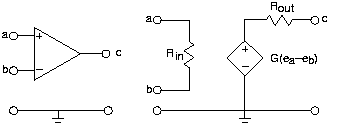
Тут вихідна напруга дорівнює посиленій версії різниці напруг вузла, що з'являються на його входах. Залежна модель джерела відображає, як працює операційний підсилювач досить добре. Як і в більшості схем активних ланцюгів, блок живлення не відображається, але повинен бути присутнім, щоб модель схеми була точною. Більшість операційних підсилювачів вимагають як позитивного, так і негативного напруги живлення для правильної роботи.

Оскільки залежні джерела не можуть бути описані як імпеданси, і оскільки залежна змінна не може «зникнути» при застосуванні правил паралельного/послідовного поєднання, спрощення ланцюга, такі як дільник струму та напруги, не слід застосовувати в більшості випадків. Аналіз схем, що містять залежні джерела, по суті, вимагає використання формальних методів, таких як метод вузлів. Використання методу вузлів для таких схем не є складним, при цьому напруга вузлів, визначених по всьому джерелу, трактується так, ніби вони відомі (як з незалежними джерелами). Розглянемо схему, зображену зверху на малюнку 3.18.3.

Малюнок 3.18.3 Верхня схема зображує операційний підсилювач в конфігурації підсилювача зворотного зв'язку. На дні знаходиться еквівалентна схема, і інтегрує модель схеми операційного підсилювача в ланцюг.

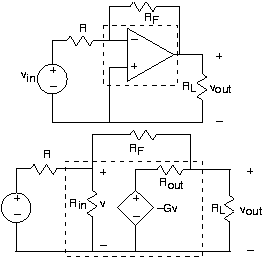
Зверніть увагу, що операційний підсилювач розміщений в схемі «догори ногами», причому його інвертує вхід вгорі і служить єдиним входом. Коли ми детальніше вивчаємо операційні підсилювачі в наступному розділі, ця конфігурація буде з'являтися знову і знову, і її корисність продемонстрована. Щоб визначити, як вихідна напруга пов'язано з вхідною напругою, застосовуємо метод вузлів. Потрібно визначити лише дві напруги вузлів - v і v _out; інші вузли знаходяться через джерела або служать еталонними. Рівняннями вузлів є:

\[\frac{v-v_{in}}{R}+\frac{v}{R_{in}}+\frac{v-v_{out}}{R_{F}}=0 \nonumber \]

\[\frac{v_{out}-(-G)v}{R_{out}}+\frac{v_{out}-v}{R_{F}}+\frac{v_{out}}{R_{L}}=0 \nonumber \]

Зауважте, що ніяких особливих міркувань не використовувалося при застосуванні методу вузла до цієї схеми залежного джерела. Вирішуючи їх, щоб дізнатися, як v _out відноситься до v _в врожайності:

\[\left ( \frac{R_{F}R_{out}}{R_{out}-GR_{F}}\left ( \frac{1}{R_{out}}+\frac{1}{R_{in}}+\frac{1}{R_{L}}\right )\left ( \frac{1}{R}+\frac{1}{R_{in}}+\frac{1}{R_{F}} \right ) -\frac{1}{R_{F}} \right )v_{out}=\frac{1}{R}v_{in} \nonumber \]

Цей вираз представляє загальне співвідношення вхід-вихід для цієї схеми, відоме як стандартна конфігурація зворотного зв'язку. Як тільки ми дізнаємося більше про операційні підсилювачі, зокрема, які його типові значення елементів, вираз значно спроститься. Зверніть увагу, що одиниці перевіряють, і що параметр G залежного джерела є безрозмірним коефіцієнтом посилення.