3.13: Функції передачі
- Page ID
- 33071
- Введення передавальної функції (АЧХ).
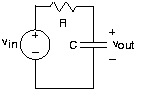
Співвідношення вихідної та вхідної амплітуди для малюнка 3.13.1, відомого як передавальна функція або частотна характеристика, задається
\[\frac{V_{out}}{V_{in}}=H(f) \nonumber \]
\[\frac{V_{out}}{V_{in}}=\frac{1}{i2\pi fRC+1} \nonumber \]
Неявним у використанні передавальної функції є те, що вхід є складною експоненціальною, а вихід також є складною експоненціальною, що має однакову частоту. Функція передачі виявляє, як схема змінює вхідну амплітуду при створенні вихідної амплітуди. Таким чином, передавальна функція повністю описує, як схема обробляє вхідний комплекс експоненціальний для отримання експоненціального вихідного комплексу. Таким чином, функція схеми підсумовується передавальною функцією. Насправді схеми часто розроблені відповідно до специфікацій функції передачі. Оскільки передавальні функції є складнозначними, залежними від частоти величинами, ми можемо краще оцінити функцію схеми, вивчивши величину та фазу її передавальної функції (див. Рис. 3.13.2 нижче)
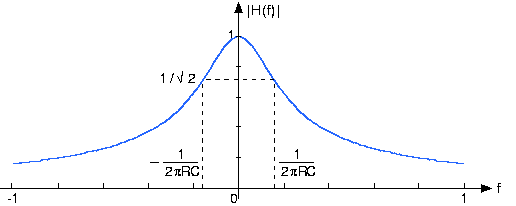
\[\left | H(f) \right |=\frac{1}{\sqrt{(2\pi fRC)^{2}+1}} \nonumber \]
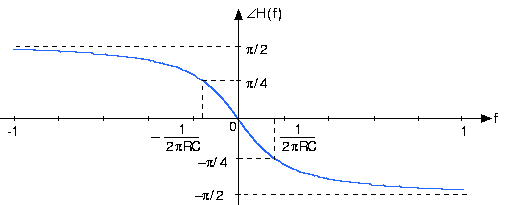
\[\angle (H(f))=-\arctan (2\pi fRC) \nonumber \]
Малюнок 3.13.2 Величина і фаза передавальної функції RC-ланцюга при RC = 1
Ця функція передачі має багато важливих властивостей і надає всі уявлення, необхідні для визначення того, як функціонує схема. Перш за все, зверніть увагу, що ми можемо обчислити частотну характеристику як для позитивних, так і для негативних частот. Нагадаємо, що синусоїди складаються з суми двох комплексних експоненціальних, одна має негативну частоту іншого. Розглянемо, як діє схема на синусоїду найближчим часом. Зверніть увагу, що величина має рівну симетрію: частина негативної частоти є дзеркальним відображенням частини позитивної частоти:
\[\left | H(-f) \right |=\left | H(f) \right | \nonumber \]
Фаза має непарну симетрію:
\[\angle H(-f)= -\angle H(f) \nonumber \]
Ці властивості цього конкретного прикладу застосовуються для всіх передавальних функцій, пов'язаних зі схемами. Отже, нам не потрібно будувати негативну частотну складову; ми знаємо, що це таке з позитивної частотної частини.
Величина дорівнює його максимальному\[\frac{1}{\sqrt{2}} \nonumber \] коефіцієнту посилення (1 при f = 0), коли 2π fRC = 1 (два долі в знаменнику величини рівні). Частота
\[f_{c}=\frac{1}{2\pi RC} \nonumber \]
визначає межу між двома робочими діапазонами.
- Для частот нижче цієї частоти схема не сильно змінює амплітуду складного експоненціального джерела.
- Для частот більше f c схема сильно послаблює амплітуду. Таким чином, коли частота джерела знаходиться в цьому діапазоні, вихід схеми має набагато меншу амплітуду, ніж у джерела.
З цих причин ця частота відома як частота зрізу. У цій схемі частота зрізу залежить тільки від твору опору і ємності. Таким чином, частота зрізу 1 кГц виникає при:
\[\frac{1}{2\pi RC}=10^{3} \nonumber \]
або
\[RC=\frac{10^{-3}}{2\pi }=1.59\times 10^{4} \nonumber \]
Таким чином, комбінації опор-ємність 1,59 кОм і 100 нФ або 10 Ом і 1,59 мкФ призводять до однакової частоти зрізу.
Зсув фаз, викликаний ланцюгом на частоті зрізу точно дорівнює -π/4. Таким чином, нижче частоти зрізу фаза мало впливає, але на більш високих частотах зсув фаз, викликаний ланцюгом, стає -π/2. Цей зсув фаз відповідає різниці між косинусом і синусом.
Ми можемо використовувати функцію передачі, щоб знайти вихід, коли вхідна напруга є синусоїдою з двох причин. Перш за все, синусоїда - це сума двох комплексних експоненціальних, кожна з яких має частоту, рівну негативній іншої. По-друге, оскільки схема лінійна, застосовується суперпозиція. Якщо джерелом є синусоїда, ми знаємо, що
\[v_{in}(t)=A\sin (2\pi ft) \nonumber \]
\[v_{in}(t)=\frac{A}{2i}\left ( e^{i2\pi ft}-e^{-(i2\pi ft)} \right ) \nonumber \]
Оскільки вхідні дані є сумою двох комплексних експоненціальних, ми знаємо, що вихід також є сумою двох подібних складних експоненціальних, єдина різниця полягає в тому, що комплексна амплітуда кожного множиться на передавальну функцію, оцінену на частоті кожної експоненціальної.
\[v_{out}(t)=\frac{A}{2i}H(f)e^{i2\pi ft}-\frac{A}{2i}H(-f)e^{-(i2\pi ft)} \nonumber \]
Як зазначалося раніше, передавальна функція найзручніше виражається в полярному вигляді:
\[H(f)=\left | H(f) \right |e^{i\angle H(f)} \nonumber \]
Крім того,
\[\left | H(-f) \right |=\left | H(f) \right | \nonumber \]
(Рівна симетрія величини) і
\[\angle H(-f)= -\angle H(f) \nonumber \]
(Непарна симетрія фази). Вираз вихідної напруги спрощує
\[v_{out}(t)=\frac{A}{2i}\left |H(f) \right |e^{i2\pi ft+\angle H(f)}-\frac{A}{2i}\left | H(f) \right |e^{(-(i2\pi ft))-\angle H(f)} \nonumber \]
\[v_{out}(t)=A\left | H(f) \right |\sin \left ( 2\pi ft+\angle (H(f)) \right ) \nonumber \]
Вихід схеми на синусоїдальний вхід також є синусоїдою, що має коефіцієнт посилення, рівний величині передавальної функції ланцюга, оціненої на частоті джерела, і фазу, рівну фазі передавальної функції на вихідній частоті. Вийде, що це опис співвідношення вхід-вихід відноситься до будь-якої лінійної ланцюга, що має синусоїдальний джерело.
Ця властивість input-output є окремим випадком більш загального результату. Показати, що якщо джерело може бути записано як уявну частину складної\[v_{in}(t)=\Im (Ve^{i2\pi ft}) \nonumber \] експоненціальної, то результат задається\[v_{out}(t)=\Im (VH(f)e^{i2\pi ft}) \nonumber \] Show, що подібний результат також має для дійсної частини.
Рішення
Ключовим поняттям є написання уявної частини як різниці між складним експоненціальним і його складним сполученим:
\[\Im (Ve^{i2\pi ft})=\frac{Ve^{i2\pi ft}-\overline{V}e^{-(i2\pi ft)}}{2i} \nonumber \]
Відповідь на\[Ve^{i2\pi ft} \nonumber \] це\[VH(f)e^{i2\pi ft} \nonumber \]
що означає відповідь на\[\overline{V}e^{-(i2\pi ft)} \nonumber \] це\[\overline{V}H(-f)e^{-(i2\pi ft)} \nonumber \]
Як\[H(-f)=\overline{H(f)} \nonumber \] принцип суперпозиції говорить, що вихід до уявної частини є\[\Im \left ( VH(f)e^{i2\pi ft} \right ) \nonumber \]
Той самий аргумент стосується реальної частини:
\[\Re (Ve^{i2\pi ft})\rightarrow \Re \left ( VH(f)e^{i2\pi ft} \right ) \nonumber \]
Поняття імпедансу виникає, коли ми припускаємо, що джерела є складними експоненціальними. Це припущення може здатися обмежувальним; що б ми зробили, якби джерело був одиничним кроком? Коли ми використовуємо імпеданси, щоб знайти функцію передачі між джерелом і вихідною змінною, ми можемо вивести з неї диференціальне рівняння, яке пов'язує вхід і вихід. Диференціальне рівняння застосовується незалежно від того, яким джерелом може бути. Як ми вже стверджували, набагато простіше використовувати імпеданси для пошуку диференціального рівняння (оскільки ми можемо використовувати правила послідовних та паралельних комбінацій), ніж будь-який інший метод. У цьому сенсі ми нічого не втратили, тимчасово прикидаючись, що джерело є складним експоненціальним.
Насправді ми також можемо вирішити диференціальне рівняння, використовуючи імпеданси! Таким чином, незважаючи на очевидну обмежувальність імпедансів, припускаючи складні експоненціальні джерела насправді цілком загальні.
