Skip to main content
LibreTexts - Ukrayinska

1.5: Проблеми введення

  1. Last updated
  2. Save as PDF
  • Page ID
    32914

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Проблеми впровадження в сигнали і системи.

    Значення RMS

    Середньоквадратичне значення періодичного сигналу визначено як

    \[s = \sqrt{\frac{1}{T}\int_{0}^{T}s^{2}(t)dt} \nonumber \]

    де T визначається як період сигналу: найменше додатне число таке, що

    \[s(t)= s(t+T) \nonumber \]

    1. Що таке період

    \[s(t)= A\sin (2\pi f_{0}t+\varphi ) \nonumber \]

    1. Яке середньоквадратичне значення цього сигналу? Як це пов'язано з піковим значенням?
    2. Який період і середньоквадратичне значення зображуваної квадратної хвилі, узагальнено позначається sq (t)?

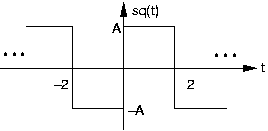
    1. Оглянувши будь-який пристрій, який ви підключаєте до розетки, ви побачите, що він має маркування «110 вольт змінного струму». Яке вираження напруги, що забезпечується настінною розеткою? Яке його середньоквадратичне значення?

    Модеми

    Слово «модем» скорочено від «модулятор-демодулятор». Модеми використовуються не тільки для підключення комп'ютерів до телефонних ліній, але і для підключення цифрових (дискретних) джерел до загальних каналів. У цій задачі ми досліджуємо простий вид модему, в якому двійкова інформація представлена наявністю або відсутністю синусоїди (наявність, що представляє «1» і відсутність «0»). Отже, передається модемом сигнал, який представляє собою єдиний біт, має вигляд

    \[x(t)= A\sin (2\pi f_{0}t), 0\leq t\leq T \nonumber \]

    У межах кожного бітового інтервалу T амплітуда дорівнює або A, або нулю.

    1. Який найменший інтервал передачі, який має сенс з частотою f 0?
    2. Припускаючи, що десять циклів синусоїди складають інтервал передачі одного біта, яка датарат цієї схеми передачі? Тепер припустимо, замість використання сигналізації «включення-виключення» ми допускаємо одне з декількох різних значень амплітуди протягом будь-якого інтервалу передачі. Якщо використовуються значення амплітуди N, яка отримана швидкість передачі даних?
    3. Класична блок-схема комунікацій відноситься і до модему. Обговоріть, як передавач повинен взаємодіяти з джерелом повідомлення, оскільки джерело виробляє літери алфавіту, а не біти.

    Розширені модеми

    Для передачі символів, таких як букви алфавіту, RU комп'ютерні модеми використовують дві частоти (1600 і 1800 Гц) і кілька амплітудних рівнів. Передача надсилається протягом періоду часу T (відомий як інтервал передачі або боди) і дорівнює сумі двох амплітудно-зважених носіїв.

    \[x(t)= A_{1}\sin (2\pi f_{1}t) + A_{2}\sin (2\pi f_{2}t), 0\leq t\leq T \nonumber \]

    Ми надсилаємо послідовні символи, вибираючи відповідну комбінацію частоти та амплітуди, і відправляючи їх один за іншим.

    1. Який найменший інтервал передачі, який має сенс використовувати з частотами, наведеними вище? Іншими словами, яким має бути Т, щоб відбувалося ціле число циклів носія?
    2. Sketch (за допомогою Matlab) сигнал, який модем виробляє протягом декількох інтервалів передачі. Переконайтеся, що осі позначені.
    3. Використовуючи інтервал передачі сигналу, скільки рівнів амплітуди потрібно для передачі символів ASCII при датарейті 3200 біт/с? Припустімо використання розширеного (8-бітного) коду ASCII.
    Примітка

    Використовується дискретний набір значень для A 1 і A 2. Якщо у нас є значення N 1 для амплітуди A 1, і N 2 значення для A 2, ми маємо N 1 N 2 можливі символи, які можуть бути відправлені протягом кожного T другого інтервалу . Щоб перетворити це число в біти (основну одиницю інформації інженери використовують для кваліфікації речей), обчислити:

    \[\log _{2}(N_{1}N_{2}) \nonumber \]