Skip to main content
LibreTexts - Ukrayinska

1.2: Сигнали представляють інформацію

  1. Last updated
  2. Save as PDF
  • Page ID
    32900

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • Коротке обговорення інформації та сигналів.
    • Введення в поняття безперервних і дискретно-часових сигналів.

    Будь то аналогова чи цифрова, інформація представлена фундаментальною величиною в електротехніці: сигналом. Зазначено в математичному плані, сигнал - це просто функція. Аналогові сигнали мають безперервне значення; цифрові сигнали - дискретні. Незалежною змінною сигналу може бути час (мова, наприклад), пробіл (зображення), або цілі числа (позначають послідовність букв і цифр в футбольному рахунку).

    Аналогові сигнали

    Аналогові сигнали зазвичай є сигналами, визначеними через безперервну незалежну змінну (и). Мова виробляється вашими голосовими зв'язками, захоплюючими акустичними резонансами у вашому голосовому тракті. Результатом є хвилі тиску, що поширюються в повітрі, і мовний сигнал, таким чином, відповідає функції, що має незалежні змінні простору і часу і значення, що відповідає тиску повітря:\[s(x,t) \nonumber \]
    Тут ми використовуємо векторні позначення\[x \nonumber \]
    для позначення просторових координат.

    Коли ви записуєте когось, що говорить, ви оцінюєте мовний сигнал у певному просторовому місці,\[x_{0} \nonumber \]
    скажімо.

    Приклад отриманої форми хвилі\[s(x_{0},t) \nonumber \]

    показано на малюнку 1.2.1:

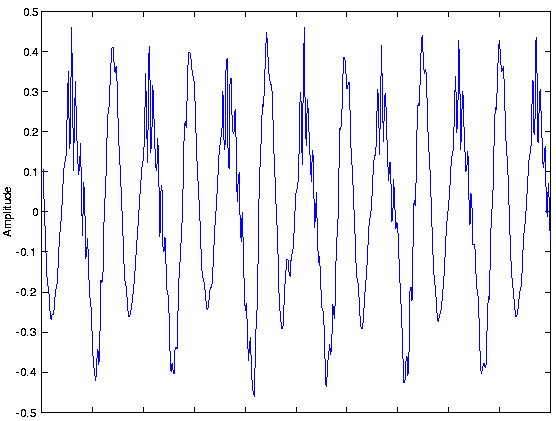
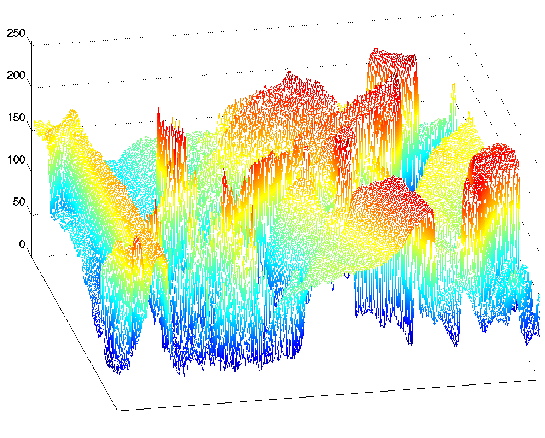
    Малюнок 1.2.1 Амплітуда мовного сигналу відноситься до крихітних варіацій тиску повітря. Показаний запис голосної «е» (як у «мова»).

    Фотографії є статичними і є безперервно-значними сигналами, визначеними у просторі. Чорно-білі зображення мають лише одне значення в кожній точці простору, що дорівнює його оптичним властивостям відбиття. На малюнку 1.2.2 показано зображення, що демонструє, що воно (і всі інші зображення також) є функціями двох незалежних просторових змінних.

    (а) (б)

    Малюнок 1.2.2 Зліва - класичне зображення Олени, яке повсюдно використовується в якості тестового зображення. Він містить прямі та вигнуті лінії, складну текстуру та обличчя. Праворуч - перспективне відображення зображення Лени у вигляді сигналу: функції двох просторових змінних. Кольори просто допомагають показати, які значення сигналу мають приблизно однаковий розмір. На цьому зображенні значення сигналу коливаються від 0 до 255; чому це так?

    Кольорові зображення мають значення, які виражають, як відбивна здатність залежить від оптичного спектра. Художники давно виявили, що змішування комбінацій так званих основних кольорів - червоного, жовтого та синього - може створювати дуже реалістичні кольорові зображення. Таким чином, сьогодні зображення зазвичай розглядаються як мають три значення в кожній точці простору, але використовується інший набір кольорів: Скільки червоного, зеленого та синього присутній. Математично кольорові зображення багатозначні - векторні значення - сигнали:

    \[s(x)=\left ( r(x),g(x),b(x) \right )^{T} \nonumber \]

    Цікаві випадки предостатньо, коли аналоговий сигнал залежить не від безперервної змінної, наприклад часу, а від дискретної змінної. Наприклад, показання температури, що знімаються щогодини, мають безперервні аналогові значення, але незалежна змінна сигналу є (по суті) цілими числами.

    Цифрові сигнали

    Слово «цифровий» означає дискретно-значний і має на увазі, що сигнал має цілозначну незалежну змінну. Цифрова інформація включає в себе цифри і символи (символи, набрані на клавіатурі, наприклад). Комп'ютери покладаються на цифрове подання інформації для маніпулювання та перетворення інформації. Символи не мають числового значення, і кожен представлений унікальним номером. Код символів ASCII має символи верхнього та нижнього регістру, цифри, розділові знаки та різні інші символи, представлені семибітовим цілим числом. Наприклад, ASCII код представляє букву

    Слово «цифровий» означає дискретно-значний і має на увазі, що сигнал має цілозначну незалежну змінну. Цифрова інформація включає в себе цифри і символи (символи, набрані на клавіатурі, наприклад). Комп'ютери покладаються на цифрове подання інформації для маніпулювання та перетворення інформації. Символи не мають числового значення, і кожен представлений унікальним номером. Код символів ASCII має символи верхнього та нижнього регістру, цифри, розділові знаки та різні інші символи, представлені семибітовим цілим числом. Наприклад, код ASCII представляє букву a як число 97, а букву A - 65. У таблиці 1.2.1 наведено міжнародну конвенцію про асоціювання символів з цілими числами.

    00 нуль 01 сох 02 stx 03 і т.д. 04 Еот 05 енк 06 назад 07 Бел
    08 бс 09 хіт 0А нл 0Б vt 0С нп 0D кр 0Е тому 0Ф сі
    10 dle 11 dc1 12 dc2 13 dc3 14 дк 4 15 нак 16 син 17 ETB
    18 автомобіль 19 ем 1А суб 1Б еск 1С фс 1D gs 1Е rs 1Ф нам
    20 сп 21 ! 22 « 23 # 24 $ 25 % 26 & 27 '
    28 ( 29 ) 2А * 2B + 2C , 2D - 2Е . 2F /
    30 0 31 1 32 2 33 3 34 4 35 5 36 6 37 7
    38 8 39 9 3А : 3Б ; 3C < 3D = 3Е > 3F ?
    40 @ 41 A 42 Б 43 C 44 D 45 Е 46 F 47 Г
    48 Ч 49 Я 4А J 4Б К 4C Л 4D М 4Е П 4Ф 0
    50 Р 51 Q 52 Р 53 S 54 Т 55 У 56 V 57 Ш
    58 Х 59 У 5А Z 5Б [ 5C \ 5D ] 5Е ^ 5F _
    60 ' 61 a 62 б 63 c 64 d 65 е 66 f 67 г
    68 ч 69 я 6А j 6Б к 6C л 6D м 6Е п 6F o
    70 р 71 q 72 р 73 s 74 т 75 у 76 v 77 ш
    78 х 79 у 7А z 7Б { 7C | 7D } 7Е ~ 7F дель

    Таблиця 1.2.1 Таблиця перекладу ASCII показує, як стандартні символи клавіатури представлені цілими числами. У парах стовпців ця таблиця відображає спочатку так званий 7-бітний код (скільки символів в семибітному коді?) , то символ, який представляє число. Числові коди представлені в шістнадцятковому (база-16) позначенні. Мнемонічні символи відповідають керуючим символам, деякі з яких можуть бути знайомими (наприклад, cr для повернення каретки), а деякі ні (bel означає «дзвін»).

    Дописувач

    • Контрібі OpenStax