6.3: Збереження рівняння моменту моменту

Рекомендованою відправною точкою для застосування принципу збереження моменту моменту є швидкісна форма рівняння: $$\frac{d \mathbf{L}_{O, \text { sys }}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left(\mathbf{r}_{i} \times \mathbf{V}_{i}\right) \dot{m}_{i} - \sum_{out} \left(\mathbf{r}_{e} \times \mathbf{V}_{e}\right) \dot{m}_{e} \nonumber$$ де$\mathbf{L}_{O, \text { sys}}$ система кутового моменту про точку$O$,$\mathbf{M}_{O}$ - швидкість транспортування кутового моменту про точку$O$ з моментами, і$\dot{m}(\mathbf{r} \times \mathbf{V})$ це швидкість транспортування кутового моменту про точку$O$ з масовим потоком через межу.

Застосовуючи форму швидкості збереження рівняння моменту моменту, існує безліч моделюючих припущень, які будуть використані для спрощення основного рівняння для конкретних систем. Як завжди, ви повинні зосередитися на розумінні фізичного значення припущень і того, як вони спрощують рівняння для даної системи. Не варто просто запам'ятовувати результати.

Стаціонарна система: Якщо система працює в стаціонарних умовах, всі інтенсивні властивості та взаємодії не залежать від часу. Коли це припущення застосовується до збереження рівняння моменту моменту, ми маємо

$$\begin{align*} \underbrace{ \cancel{ \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} }^{=0} }_{\begin{array}{c} \mathbf{L}_{O, \text{ sys}} \text{ is} \\ \text{constant} \end{array} } &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \dot{m}_i - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \dot{m}_e \\ 0 &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \dot{m}_i - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \dot{m}_e \end{align*} \nonumber$$

Закрита система: Замкнута система не має потоку на кордоні, тому збереження рівняння моменту моменту зводиться до наступного: $$\begin{align*} \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} &= \sum_{j} \mathbf{M}_{O, \ j} + \sum_{in} \left( \mathbf{r}_i \times \mathbf{V}_i \right) \cancel{ \dot{m}_i }^{=0} - \sum_{out} \left( \mathbf{r}_e \times \mathbf{V}_e \right) \cancel{ \dot{m}_e }^{=0} \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{dt} &= \sum_{j} \mathbf{M}_{O, \ j} \end{align*} \nonumber$$

Щоб зробити будь-які подальші спрощення, необхідно володіти додатковою інформацією або робити припущення про кінематику рухомої системи. Якщо ми можемо припустити, що плоска система перекладається, то $$\left. \begin{array}{c} \mathbf{L}_{O, \text{ sys}} = m_{\text{sys}} \left( \mathbf{r}_{G} \times \mathbf{V}_{G}\right) \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \end{array} \right\} \quad \rightarrow \quad m_{\text{sys}} \frac{d \left(\mathbf{r}_{G} \times \mathbf{V}_{G} \right)}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \nonumber$$

Якщо ми можемо припустити, що площина, жорстка система обертається навколо$z$ осі (осі), яка проходить через центр маси системи, то $$\left. \begin{array}{c} \mathbf{L}_{O, \text{ sys}} = \omega_{z} I_{G} \mathbf{k} \\ \frac{d \mathbf{L}_{O, \text{ sys}}}{d t} = \sum_{j} \mathbf{M}_{O, \ j} \end{array}\right\} \quad \rightarrow \quad \frac{d\left(\omega_{z} I_{G} \mathbf{k}\right)}{d t}=\sum_{j} \mathbf{M}_{O, \ j} \nonumber$$ де$\mathbf{k}$ знаходиться вектор одиниці точок в позитивному напрямку$z$ -осі.

Моделювання реакцій на опорах і з'єднаннях:

Однією із суттєвих проблем при виборі системи для передачі імпульсу є виявлення взаємодій між системою та її оточенням. Які саме обмеження щодо того, як імпульс передається через межу при конкретних взаємодіях? Контактні сили на кордоні системи іноді називають реакціями, особливо в місцях, де межа розрізає опору або з'єднання. Відповідно до Beer and Johnston$^{1}$, реакції можна класифікувати за трьома широкими категоріями:

(а) Сила з відомою лінією дії. Багато з'єднань задовольняють цій умові серед них ролики, коромисла, поверхні без тертя, короткі ланки і троси, коміри на стрижнях без тертя і штирі без тертя в пазах. Кожна з цих реакцій характеризується здатністю лише транспортувати лінійний імпульс силою в єдиному, чітко ідентифікованому напрямку. (Див. Малюнок$\PageIndex{1}$).

(б) Сила невідомого напрямку та величини. Апаратні засоби або з'єднання, які забезпечують цей тип реакції, включають фрикційні штифти в підігнаних отворах, фрикційні кулькові та розеткові з'єднання, шарніри та шорсткі поверхні (Хоча поверхні без тертя передають лише силу, нормальну до поверхні, тертя вносить сили зсуву на поверхні.)

(c) Сила невідомого напрямку і величини і пара. Цей останній тип реакції зазвичай називають фіксованою опорою. Відмінним прикладом є реакція землі на телефонний стовп, застряглий вертикально в землі. Коли ви натискаєте телефонний полюс у будь-якому напрямку, земля чинить три сили на полюс - горизонтальну силу зсуву, вертикальну нормальну силу та розподілену силу, яка є силовою парою. Пара, як було показано раніше, передає тільки кутовий момент.

Малюнок$\PageIndex{1}$: Поверхневі силові реакції.

Як і слід було очікувати, ці реакції можна побачити в повсякденному житті, якщо хтось спостережливий. Озирніться навколо вас прямо зараз і подивіться, чи зможете ви знайти фізичний зв'язок, який потрапляє в кожну з цих категорій. Наприклад, подивіться на заклинатель або колесо на стільці столу або петлю на дверях. Наступного разу, коли ви їдете під естакадою по шосе, подивіться, як дорожнє полотно моста спирається на колони. Ви, швидше за все, побачите ролик.

$^{1}$Пиво Ф.П. та Джонстон-молодший, векторна механіка для інженерів: статика, 6-е видання, Макгроу-Хілл, Нью-Йорк, 1996.

Приклад — Яка реакція!

Визначте реакції при$A$ і$C$. Припустимо, вага механізму незначний і що всі суглоби без тертя.

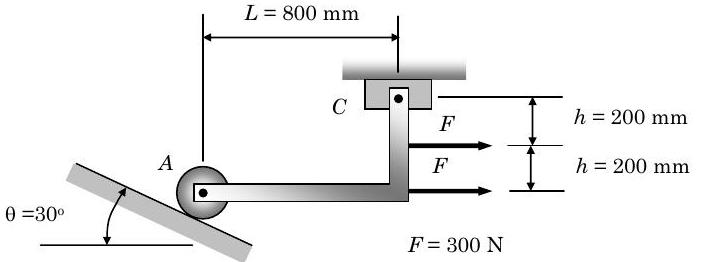
Малюнок$\PageIndex{2}$: Г-подібна планка спирається на два кінці і має точкові навантаження, прикладені в двох точках.

Рішення

Відомо: специфічний пристрій з заданими навантаженнями.

Знайти: Реакції (величина і напрямок) в точках$A$ і$C$.

Дано: Див. малюнок, намальований вище. (Зверніть увагу, як всі фізичні величини були надані символи.)

Аналіз:

Стратегія.$\rightarrow$ Оскільки ця проблема стосується сил, то як мінімум вона зажадає лінійного імпульсу і, можливо, кутового моменту. (Остання частина - це піддавка, оскільки ця проблема знаходиться в розділі кутового моменту. На жаль, проблеми в реальному житті ніколи не приходять з номером глави.)

$\rightarrow$Закрита система, що не деформується, включаючи$C$ штифтове з'єднання, ролик$A$ та сполучну планку.
Властивість для підрахунку$\rightarrow$ Лінійний і кутовий імпульс
Часовий інтервал$\rightarrow$ Спробуйте форму швидкості. (Імпульс протікає через цю систему.)

Система, намальована нижче, показує реакції$A$$C$ та всі відповідні розміри на малюнку. Припускаючи, що це замкнута та стійка система, лінійні та рівняння моменту моменту стають такими: $$0=\sum_{j} \mathbf{F}_{j} \quad \text { and } \quad 0=\sum_{j} \mathbf{M}_{0, \ j} \nonumber$$ (Чи могли б ви явно показати, як ці два рівняння були отримані з огляду на наведені вище припущення?)

Малюнок$\PageIndex{3}$: Діаграма вільного тіла.

Перш ніж писати рівняння компонентів у скалярній формі, ми повинні чітко вказати систему координат і те, що ми приймаємо як позитивні напрямки. Це робиться за допомогою малої системи координат на малюнку. Зверніть увагу, що ми приймаємо проти годинникової стрілки (CCW) як позитивний напрямок для кутового моменту.

Тепер дивимося на$x$ -імпульс:

$$\boxed{ \rightarrow + } \quad\quad 0 = R_{A}(\sin \theta) + 2 F + R_{C x} \quad \rightarrow \quad -2 F = R_{A}(\sin \theta)+R_{C x} \quad \rightarrow \quad -(600 \mathrm{~N}) = R_{A}\left(\sin 30^{\circ}\right)+R_{C x} \nonumber$$

Для$y$ -імпульсу:

$$\boxed{ \uparrow +} \quad\quad 0 = R_A (\cos \theta) + R_{C y} \quad \rightarrow \quad R_{C y} = - R_A \left( \cos 30 ^{\circ} \right) \nonumber$$

Це дає два рівняння для трьох невідомих —$R_{A}$,$R_{C x}$, і$R_{C y}$. Щоб отримати рівняння, що залишилося, ми повинні застосувати збереження кутового моменту.

Застосовуючи збереження кутового моменту близько Точки,$A$ ми усуваємо будь-який момент завдяки одній із прикладених сил$F$ і реакції$R_{A}$: $$\boxed{ \text {CCW }+ } \quad\quad 0=\left[ +L R_{C y} \right] + \left[-2 h R_{C x}\right] + [-h F] \quad \rightarrow \quad F=\left(\frac{L}{h}\right) R_{C y}-2 R_{C x} \quad \rightarrow \quad (300 \mathrm{~N}) = (4) R_{C y} - 2 R_{C x} \nonumber$$

Вирішуючи ці три рівняння одночасно, отримаємо наступне: $$\left. \begin{array}{rlrl} -(600 \mathrm{~N}) & =R_{A} \sin 30^{\circ}-2 R_{C x} \\ R_{C y} &= -R_{A} \cos 30^{\circ} \\ (300 \mathrm{~N}) &= R_{A} \sin 30^{\circ}+R_{C x} \end{array} \right\} \quad \rightarrow \quad \begin{aligned} R_{A} &= 365.2 \mathrm{~N} \\ R_{C x} &= -782.6 \mathrm{~N} \\ R_{C y} &= -316.3 \mathrm{~N} \end{aligned} \nonumber$$

Зверніть увагу, що реакція при$C$ відбувається в напрямку, протилежному тому, що передбачається на малюнку.

Приклад — Перехід до стіни за реакцією

Струмінь води стійко впливає на лезо, яке кріпиться до консольної балки, як показано на малюнку. Консольна балка кріпиться до стіни при$A$ і утримує лопатку нерухомо. Вода потрапляє на лезо$B$ і залишає лезо на$C$.

Маса комбінації лезо/промінь -$100 \ \text{lbm}$ з відомим центром маси в точці,$G$ розташованій на відстані$L/2$ від стіни. Вода має масову витрату$150 \text{lbm} / \text{s}$, а швидкість води однакова, що надходить і виходить з лопаті,$V_1 = V_2 = 20 \ \text{ft} / \text{s}$. Вода виходить з лопаті під кутом$30^{\circ}$ нижче горизонталі.

Інша інформація наступна:$L=5 \ \mathrm{ft}$,$d=7 \ \mathrm{ft}$, і$h=2 \ \mathrm{ft}$.

Визначте реакції на консольну балку у стіни$(A)$.

Малюнок$\PageIndex{4}$: Вода падає на вигнуте лезо, прикріплене до консольної балки, і стікає з нижнього кінця леза.

Рішення

Відомо: Вода відхиляється лезом, підтримуваним консольною балкою.

Знайти: Реакції на консольну балку біля стіни.

Дано: Див. Малюнок вище. Знову ж таки, зверніть увагу, як всі фізичні величини мають символи.

Аналіз:

Стратегія$\rightarrow$ Оскільки нас просять реакції (сили та моменти), ми повинні спробувати використовувати збереження лінійного та кутового імпульсу.

Система$\rightarrow$ Open, що не деформується система, яка включає лопатку-промінь води з водою, що протікає і назовні, як показано нижче.
Властивість підрахунку$\rightarrow$ Кутовий і лінійний імпульс (і, можливо, маса).
Часовий інтервал$\rightarrow$ Ймовірно нескінченно малий проміжок часу, тобто форма швидкості.

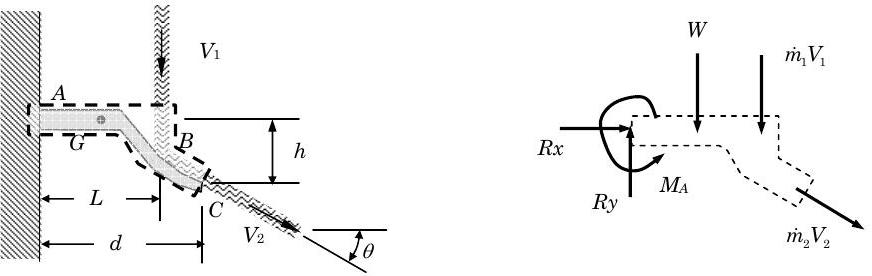
Малюнок$\PageIndex{5}$: Діаграма вільного тіла балки, лопаті та системи водопостачання.

На малюнку вище показана діаграма вільного тіла (або взаємодії системи). Зверніть увагу, що з'єднання біля стіни замінюється двома силами і моментом, оскільки з'єднання стіна-балка є нерухомою опорою. Також зверніть увагу, що масові транспорти лінійного імпульсу показані на малюнку разом з вагою, що діє в точці$G$.

Як відправну точку, давайте напишемо збереження маси і подивимося, що вона нам говорить: $$\underbrace{ \cancel{ \frac{d m_{\text{sys}}}{d t} }^{=0} }_{\text {steady state}} = \dot{m}_{1} - \dot{m}_{2} \quad \rightarrow \quad \dot{m}_{1} = \dot{m}_{2}=\dot{m} \nonumber$$ Це може здатися тривіальним результатом, але якщо ви не побачили його відразу, це не тривіально. Крім того, це лише підтверджує вашу інтуїцію.

Тепер напишемо збереження лінійного імпульсу: $$\cancel{ \frac{d \mathbf{P}_{\text{sys}}}{d t} }^{=0} = \mathbf{Rx} + \mathbf{Ry} + \mathbf{W} \ + \ \dot{m}_{1} \mathbf{V}_{1} - \dot{m} \mathbf{V}_{2} \quad \rightarrow \quad 0=\mathbf{Rx} + \mathbf{Ry} + \mathbf{W} \ + \ \dot{m}_{1} \mathbf{V}_{1} - \dot{m} \mathbf{V}_{2} \nonumber$$

Тепер записуючи скалярну форму цього рівняння, припустимо, позитивне$x$ праворуч і позитивне$y$ - вгору.

$$\begin{aligned} \boxed{\rightarrow +} \quad\quad 0 &= Rx - \dot{m}\left( V_{2} \cos \theta \right) \\ Rx &= \dot{m}\left( V_{2} \cos \theta \right) \quad \rightarrow \quad Rx = \left( 150 \ \dfrac{\mathrm{lbm}}{\mathrm{s}}\right) \left(20 \ \frac{\mathrm{ft}}{\mathrm{s}} \right) \left( \cos 30^{\circ} \right) \left(\frac{1 \ \mathrm{lbf}}{32.174 \ \dfrac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^{2}}} \right) = 80.8 \ \mathrm{lbf} \\ \\ \boxed{\uparrow +} \quad\quad 0 &= Ry - W + \dot{m}\left(-V_{1}\right) - \dot{m}\left(-V_{2} \sin 30^{\circ}\right) \\[4pt] Ry &= W + \dot{m}\left(V_{1}-V_{2} \sin 30^{\circ}\right) \\[4pt] &= W + \dot{m} V \left(1-\sin 30^{\circ}\right) \\[4pt] Ry &= \left[(100 \ \mathrm{lbm}) \left(\frac{1 \ \mathrm{slug}}{32.174 \ \mathrm{lbm}}\right) \left(32.174 \ \dfrac{\mathrm{ft}}{\mathrm{s}^{2}}\right) \right] \\[4pt] &=[100+46.6] \ \mathrm{lbf} \\[4pt] &=146.6 \ \mathrm{lbf} \end{aligned} \nonumber$$

Будьте дуже обережні до знаків на умовах, особливо до термінів масової витрати. Зверніть увагу, що перед масовими витратами залежать від$+ \ / \ -$ того, чи є потік у систему або поза нею; знаки всередині дужок щодо термінів швидкості (питомий лінійний імпульс) є результатом перекладу вектора швидкості до цієї конкретної системи координат.

З одним$M_A$, що залишився невідомим, нам потрібно застосувати збереження моменту. Хоча ми можемо підсумувати моменти про будь-яку точку, давайте використаємо точку$C$. Це має перевагу усунення кутового моменту, здійснюваного в струмені води при$C$.

$$\begin{aligned} \frac{d \mathbf{L}_{C, \text{ sys}}}{d t} &= M_{A} + \left(\mathbf{r}_{A} \times \mathbf{Rx} \right) + \left( \mathbf{r}_{A} \times \mathbf{R y}\right) + \left(\mathbf{r}_{G} \times \mathbf{W}\right) + \dot{m} \left(\mathbf{r}_{B} \times \mathbf{V}_{1}\right) \\ \boxed{\mathrm{CW} +} \quad\quad 0 &= \left(-M_{A}\right) + (+h \cdot Rx) + (d \cdot Ry) + \left[ -\left(d-\dfrac{L}{2}\right) W \right] + \dot{m} \left[-(d-L) V_{1}\right] \\ M_{A} &= (h \cdot Rx) + (d \cdot Ry) + \left( -\left(d-\frac{L}{2}\right) W \right) + \dot{m}\left[-(d-L) V_{1}\right] \\ M_{A} &= [(2 \ \mathrm{ft})(80.8 \ \mathrm{lbf})] + [(7 \ \mathrm{ft})(146.6 \ \mathrm{lbf})] + \left[ -\left(7-\frac{5}{2}\right)(\mathrm{ft})(100 \ \mathrm{lbf}) \right] + \left(150 \ \frac{\mathrm{lbm}}{\mathrm{s}}\right) \left[-(2 \ \mathrm{ft})\left(20 \ \frac{\mathrm{ft}}{\mathrm{s}}\right) \right] \\ &=(161.6 \ \mathrm{ft} \cdot \mathrm{lbf}) + (1026.2 \ \mathrm{ft} \cdot \mathrm{lbf}) + (-450 \ \mathrm{ft} \cdot \mathrm{lbf}) + \underbrace{ \left(-6000 \ \frac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^2} \right) \left( \frac{1 \ \mathrm{lbf}}{32.174 \ \dfrac{\mathrm{lbm} \cdot \mathrm{ft}}{\mathrm{s}^2}} \right) }_{= -186.5 \ \mathrm{ft} \cdot \mathrm{lbm}} \\ &=[161.6+1026.2-450-186.5] \ \mathrm{ft} \cdot \mathrm{lbf} \\ \\ M_{A} &= 551.3 \ \mathrm{ft} \cdot \mathrm{lbf} \end{aligned} \nonumber$$

Подібні коментарі щодо знаків стосуються кутового моменту, наведеного для лінійного імпульсу.

Таким чином реакції при$A$ є$Rx = 80.8 \ \mathrm{lbf}$$Ry =146.6 \ \mathrm{lbf}$, і$M_{A} = 551.3 \ \mathrm{ft} \cdot \mathrm{lbf}$ в напрямках, як зазначено на схемі.

Приклад — Чайові коробки

Вас попросили допомогти перемістити картотеку, натиснувши його на підлогу. На щастя для вас підлога має дуже низькі коефіцієнти тертя ($\mu_{\text {static}} = 0.3$і$\mu_{\text {kinetic}}=0.1$). Картотечна шафа$0.3 \mathrm{~m}$ широкий і$1.6 \mathrm{~m}$ високий і має масу$100 \mathrm{~kg}$. Ви будете штовхати його в положенні над підлогою,$3 / 4$ рівному його висоті.

(а) Визначте силу,$F$ необхідну для переміщення шафи. Чи почне він кінчати, перш ніж прослизне?

(б) Якщо він кінчає перед тим, як прослизне, яка сила$F$ потрібна, щоб почати перекидання стаціонарного шафи?

(c) Якщо він ковзає перед кінчиками,$F$ яке максимальне зусилля можна застосувати до ковзання наконечників шафи?

Рішення

Відомо: по підлозі проштовхують картотечну шафу.

Знайти:

(а) Сила, необхідна для ковзання шафи

(b) Якщо він кінчить, перш ніж він ковзає, сила, необхідна для початку перекидання

(c) Якщо він ковзає перед кінчиками, максимальне зусилля, яке можна застосувати до ковзання наконечників шафи

Дано: $$\begin{aligned} &h=1.6 \mathrm{~m} \quad m=100 \mathrm{~kg} \\ &L=0.3 \mathrm{~m} \\ &d=1.2 \mathrm{~m} \\ &G \text { in center of rectangle } \\ \\ &\text {Positive directions on coordinate system } \end{aligned} \nonumber$$

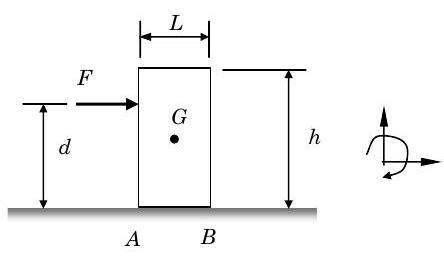
Малюнок$\PageIndex{6}$: Позначена діаграма, що показує всю надану інформацію

Аналіз

Стратегія$\rightarrow$ Спробуйте зберегти лінійний і кутовий імпульс, так як ми розглядаємо сили тертя і рух і перекидання.

Система$\rightarrow$ Закрита, що не деформується система, яка включає лише шафа.
Властивість підрахунку$\rightarrow$ Лінійний імпульс і момент моменту.
Часовий інтервал.$\rightarrow$ Ймовірно, форма ставки, так як нас цікавлять сили.

Для початку нам потрібно намалювати схему вільного тіла. Зверніть увагу, що напрямок сили тертя по дну шафи протистоїть руху шафи. Ви також повинні помітити, що$F_{\mathrm{N}}$ нормальна сила на дні шафи може діяти в будь-якому місці між$A$ і в$B$ залежності від величини прикладеної сили$F$. Зрозуміло$F$, що коли дорівнює нулю, нормальна сила прикладається безпосередньо під центром маси.

Для початку визначимося, яка сила призведе до того, що шафа прослизне. Для цього ми застосовуємо збереження лінійного імпульсу до стаціонарної, замкнутої системи.

$$\underbrace{ \cancel{ \frac{d \mathbf{P}_{\text{sys}}}{dt} }^{=0} }_{ \begin{array}{c} \mathbf{P}=0 \\ \text{a constant} \end{array} } = \sum_{j} \mathbf{F}_{j} + \underbrace{ \cancel{ \sum_{\text {in}} \dot{m}_{i} \mathbf{V}_{i} - \sum_{\text {out}} \dot{m}_{e} \mathbf{V}_{e} }^{=0} }_{\text {closed system, no mass flow}} \quad \rightarrow \quad 0 = \mathbf{F} + \mathbf{F}_{f} + \mathbf{F}_{\mathrm{N}} +m \mathbf{g} \nonumber$$

Де сила тертя повинна дорівнювати максимально можливій статичній силі тертя $$\begin{array}{lll} & \boxed{\rightarrow +} \quad & 0 =-F_{f}+F & \rightarrow \quad F=F_{f} \leq \mu_{\text {static}} F_{N} \\ & \boxed{\uparrow +} & 0=-m g+F_{N} & \rightarrow \quad F{N}=mg \\ & F=F_{f} \leq \mu_{\text {static}} m g = (0.3)\left[(100 \mathrm{~kg})\left(9.81 \ \frac{\mathrm{m}}{\mathrm{s}^{2}}\right)\right] = 294.3 \mathrm{~N} \end{array} \nonumber$$

Таким чином, мінімальне зусилля, яке потрібно докласти, щоб змусити шафу ковзати, є$294.3 \mathrm{~N}$.

Тепер, щоб визначити, чи це поради, застосуйте збереження кутового моменту до тієї ж системи. Для цього ми повинні визнати, що якраз у нього починає кінчик (перекидання насувається) нормальна сила діє в точці$B$ (права сторона шафи). Отже, давайте обчислимо кутовий момент про точку$B$ і вирішимо для сили, яка повинна бути застосована до наконечника шафи, припускаючи, що він нерухомий,$F_{\text {tip}}$.

$$\begin{array}{lll} & \underbrace{ \cancel{ \dfrac{d \mathbf{L}_{B, \text{ sys}}}{dt} }^{=0} }_{\begin{array}{c} \mathbf{L}=0 \text{ since} \\ \text{stationary} \end{array}} = \sum_j \mathbf{M}_{B, \ j} \ + \underbrace{ \cancel{ \sum - \sum}^{=0} }_{\begin{array}{c} \text{Closed system} \\ \text{No mass flow terms} \end{array}} \quad & \rightarrow \quad & 0 = \left( \mathbf{r}_F \times \mathbf{F}_{\text{tip}} \right) + \left( \mathbf{r}_G \times m \mathbf{g} \right) \\ \\ & \begin{align*} \boxed{\text{CW } +} \quad\quad 0 &= \left( d \ F_{\text{tip}} \right) + \left( \frac{L}{2} mg \right) \\ F_{\text{tip}} &= \frac{1}{2} \frac{L}{d} mg \end{align*} & \rightarrow & F_{\text{tip}} = \dfrac{1}{2} \left( \dfrac{0.3 \mathrm{~m}}{1.2 \mathrm{~m}} \right) (981.0 \mathrm{~N}) = 122.6 \mathrm{~N} \end{array} \nonumber$$

Порівнюючи силу ковзання проти сили до кінчика, ми виявляємо, що сила кінчика менше, ніж сила ковзання шафи - наконечники шафи, перш ніж вона ковзає. Максимальне зусилля, яке можна докласти до шафи до його наконечників, є$122.6 \mathrm{~N}$ і шафа ніколи не зісковзне.

Відповідь на частину (c) є академічною, оскільки кабінет міністрів ніколи не прослизає за цих умов.

Коментар:

Але почекайте, нам потрібно перенести кабінет! Припустимо, ми розміщуємо шафу на деяких дуже маленьких роликових підшипниках, щоб він по суті ковзав по підлозі без статичного або кінетичного тертя. Скільки сили я можу застосувати зараз, перш ніж це поради?

Результати$y$ -momentum будуть ідентичними$\rightarrow \ F_{\mathrm{N}} = mg = 981 \mathrm{~N}$.

Результати$x$ -momentum повинні враховувати рух у$x$ напрямку, тому ми маємо$\rightarrow m \frac{d V_{G}}{d t}=F$.

Рівняння кутового моменту складніше. Спочатку ми повинні визнати, що шафа перекладається, і що при наближенні перекидання нормальна сила$F_{\mathrm{N}}$ буде діяти в правому куті:

$$\dfrac{d \mathbf{L}_{B}}{dt} = \left(\mathbf{r}_{F} \times \mathbf{F}\right) + \left(\mathbf{r}_{G} \times m \mathbf{g}\right) \quad \text { and } \quad \mathbf{L}_{B} = m \left(\mathbf{r}_{G} \times \mathbf{V}_{G}\right) \quad\quad\quad\quad\quad\quad\quad \nonumber$$

$$\begin{align*} \boxed{ \text{CW }+ } \quad\quad \dfrac{d}{dt} \underbrace{ \left[ m \left( \dfrac{h}{2} V_G \right) \right] }_{\begin{array}{c} \text{Angular momentum} \\ \text{of system about} \\ \text{point }B \end{array}} &= \underbrace{ \left( d \ F \right) }_{\begin{array}{c} \text{Moment of} \\ \text{force } F \text{ about} \\ \text{point }B \end{array}} + \underbrace{ \left( - \dfrac{L}{2} mg \right) }_{\begin{array}{c} \text{Moment of} \\ \text{the weight about} \\ \text{point }B \end{array}} \\[4pt] m \dfrac{d}{dt} \left( \dfrac{h}{2} V_G \right) &= dF - \dfrac{L}{2} mg \\[4pt] m \dfrac{h}{2} \dfrac{d V_G}{dt} &= dF - \dfrac{L}{2} mg \quad\quad\quad \rightarrow \quad\quad\quad \begin{array}{l} \\{ } \\ F = \dfrac{m}{2} \dfrac{h}{d} \dfrac{d V_G}{dt} + \dfrac{m}{2} \dfrac{L}{2} g \\[4pt] F = \dfrac{m}{2} \left( \dfrac{h}{d} \right) \left[ \dfrac{d V_G}{dt} + g \left( \dfrac{L}{h} \right) \right] \end{array} \end{align*} \nonumber$$

Тепер нам потрібно використовувати наші результати від$x$ -momentum, щоб усунути термін прискорення. $$\begin{aligned} F = \frac{m}{2} \left(\frac{h}{d}\right) \left[\frac{dV_{G}}{dt} + g \left(\frac{L}{h}\right) \right] &= \frac{m}{2}\left(\frac{h}{d}\right) \underbrace{\left[\left(\frac{F}{m}\right)+g\left(\frac{L}{h}\right)\right]}_{\begin{array}{c} \text { Here's where we } \\ \text { made the substitution } \end{array}} \\[4pt] \begin{array}{c} F - \dfrac{m}{2} \left(\dfrac{h}{d}\right) \left(\dfrac{F}{m}\right) = \dfrac{m}{2} \left(\dfrac{h}{d}\right) \left(\dfrac{L}{h}\right) g \\[4pt] F \left[1-\dfrac{1}{2}\left(\dfrac{h}{d}\right)\right] = \dfrac{m}{2} \left(\dfrac{L}{d}\right) g \\ { } \\ { } \end{array} \quad\quad\quad &\rightarrow \quad\quad\quad F = \dfrac{\dfrac{m}{2} \left(\dfrac{L}{d}\right) g}{\left[1-\dfrac{1}{2}\left(\dfrac{h}{d}\right)\right]} = (m g) \dfrac{\dfrac{1}{2} \left(\dfrac{L}{d}\right)}{\left[1-\dfrac{1}{2} \left(\dfrac{h}{d}\right)\right]} \end{aligned} \nonumber$$

Тепер підставляючи числові значення, ми маємо $$F = (mg) \frac{\dfrac{1}{2}\left(\dfrac{L}{d}\right)}{\left[1 - \dfrac{1}{2} \left(\dfrac{h}{d}\right)\right]} =(981 \mathrm{~N}) \frac{\dfrac{1}{2}\left(\dfrac{0.3}{1.2}\right)}{\left[1 - \dfrac{1}{2} \left(\dfrac{1.6}{1.2}\right)\right]} = 367.9 \mathrm{~N} \nonumber$$ Зверніть увагу, що значення$F$ залежить від ваги об'єкта$h / d$, співвідношення і співвідношення$L / d$. Що відбувається, коли$d=h / 2$? Що це означає фізично? А як щодо коли$L=0$? Що це означає?

Приклад - це поворот!

Два металевих циліндра$A$ і$B$ підвішені до шківа без тертя. Циліндр$A$ має масу$30 \mathrm{~kg}$ і циліндр$B$ має масу$60 \mathrm{~kg}$. Шків по суті являє собою плоский диск діаметром$0.5 \mathrm{~m}$ і масою$10 \mathrm{~kg}$. Кабелі мають незначну масу.

Малюнок$\PageIndex{7}$: Два циліндра підвішені до шківа без тертя.

Спочатку циліндри стаціонарні. Якщо вони раптово звільнилися, розрахуйте прискорення циліндрів.

Рішення

Відомо: дві маси, підвішені до шківа, раптом починають рухатися.

Знайти: Прискорення циліндрів після їх звільнення.

Дано: Див. Малюнок вище.

$$\begin{align*} & \text{Diameter of the pulley} = D = 0.5 \mathrm{~m}\\ & \text{Mass of the pulley} = m_{\text {Pulley}} = 10 \mathrm{~kg} \\ & \text{Mass of cylinder } A = m_{\mathrm{A}} = 30 \mathrm{~kg} \\ & \text{Mass of cylinder } B = m_{\mathrm{B}} = 60 \mathrm{~kg} \end{align*} \nonumber$$

Аналіз:

Стратегія$\rightarrow$ Спробуйте кутовий імпульс, оскільки шків повертається, і нам не сказали ігнорувати масу шківа.
Система$\rightarrow$ Закрита система, що містить циліндри, трос та шків.
Властивість підрахунку$\rightarrow$ Кутовий
момент Часовий інтервал$\rightarrow$ Початок з рівняння швидкості

Діаграма вільного тіла показана нижче, із зазначенням відомих сил на систему. Оскільки це замкнута система, то немає масових передач імпульсу. Дивіться стрілки на схемі, щоб вказати позитивні напрямки для$x_{A}, x_{B}$, і$\omega$.

Малюнок$\PageIndex{8}$: Схема вільного тіла системи, що складається з шківа і прикріплених до нього блоків.

Записуючи кутовий момент навколо осі обертання шківа для системи і припускаючи, що обертання за годинниковою стрілкою позитивне, ми отримаємо наступний результат:

$$\begin{aligned} \frac{d \mathbf{L}_{0, \text{ sys}}}{d t} &= \left(\mathbf{r}_{A} \times \mathbf{W}_{A}\right) + \left(\mathbf{r}_{B} \times \mathbf{W}_{B}\right) \\ \text{where} \quad\quad\quad \mathbf{L}_{0, \text{ sys}} &= m_{A} \left(\mathbf{r}_{A} \times \mathbf{V}_{A}\right) + m_{B} \left(\mathbf{r}_{B} \times \mathbf{V}_{B}\right) + \mathbf{\omega} I_{G} \\[4pt] \\ \boxed{\text{CW } +} \quad\quad \frac{d L_{0, \ \mathrm{sys}}}{d t} &= \left(\dfrac{D}{2} W_{B}\right) + \left(-\dfrac{D}{2} W_{A}\right) \\[4pt] \text{where} \quad\quad\quad L_{0, \mathrm{sys}} &= \underbrace{ \left(\dfrac{D}{2} m_{A} V_{A}\right) }_{\begin{array}{c} \text{Angular momentum of} \\ \text{Cylinder A about axle with} \\ \text{positive velocity } V_A \text{ upward} \end{array}} + \underbrace{ \left(\dfrac{D}{2} m_{A} V_{A}\right) }_{\begin{array}{c} \text{Angular momentum of} \\ \text{Cylinder B about axle with} \\ \text{positive velocity } V_B \text{ downward} \end{array}} + \underbrace{ \omega I_{G} }_{\begin{array}{c} \text{Angular momentum of} \\ \text{the pulley assuming positive} \\ \omega \text{ is in clockwise direction} \end{array}} \end{aligned} \nonumber$$

Тепер підставляючи систему кутового моменту в баланс імпульсу, ми маємо

$$\boxed{\mathrm{CW} \ +} \quad\quad \frac{d}{dt} \left[ \left(\frac{D}{2} m_{A} V_{A}\right) + \left(\frac{D}{2} m_{A} V_{A}\right) + \omega I_{G}\right] = \left(\frac{D}{2} W_{B}\right) + \left(-\frac{D}{2} W_{A}\right) \nonumber$$

Це рівняння можна ще більше спростити, визнавши, що тільки швидкості є константами, тому виведення констант поза похідною і ділення через на$D / 2$ дає наступне $$\boxed{\mathrm{CW} \ +} \quad\quad m_{A} \frac{d V_{A}}{d t} + m_{B} \frac{d V_{B}}{d t} + \left(\frac{2}{D}\right) I_{G} \frac{d \omega}{d t} = -W_{A}+W_{B} \nonumber$$

Щоб піти далі, ми повинні співвіднести поступальну і обертальну швидкості. Припускаючи, що позитивний напрямок обертання - це годинникова стрілка, що відповідає стрілкам швидкості на діаграмі, ми маємо наступне: $$V_{A} = V_{B} = \omega (D / 2) \nonumber$$ Використання цього результату для заміни$V_{\text {В }}$ і$\omega$ в балансі кутового моменту дає наступне:

$$\begin{aligned} \boxed{\mathrm{CW} \ +} \quad\quad m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{B}}{dt} + \left(\frac{2}{D}\right) I_{G} \frac{d}{dt} \left(\frac{2}{D} V_{A}\right) &= W_{B}-W_{A} \\[4pt] m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{A}}{dt} + \left(\frac{2}{D}\right)^{2} I_{G} \frac{d V_{A}}{d t} &= W_{B}-W_{A} \end{aligned} \nonumber$$

Для закінчення ми повинні записати ваги і момент інерції маси шківа в перерахунку на їх масу наступним чином:

$$\begin{aligned} m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{A}}{dt} + \left(\frac{2}{D}\right)^{2} I_{G} \frac{d V_{A}}{dt} &= W_{B}-W_{A} \\[4pt] m_{A} \frac{d V_{A}}{dt} + m_{B} \frac{d V_{B}}{dt} + \left(\frac{2}{D}\right)^2 \underbrace{ \left[\frac{1}{2} m_{\text {Pulley }} \left(\frac{D}{2}\right)^{2}\right] }_{\begin{array}{c} I_G \text{ for the pulley treated} \\ \text{as a disk} \end{array}} \frac{d V_A}{dt} &= m_B \ g - m_A \ g \\ m_A \frac{d V_A}{dt} + m_B \frac{d V_A}{dt} + \left( \frac{m_{\text{Pulley}}}{2} \right) \left[\frac{d V_A}{dt}\right] &= \left(m_B - m_A\right) g \\[4pt] \frac{d V_A}{dt} &= \frac{ \left(m_B - m_A\right) }{\left(m_A + m_B + \dfrac{m_{\text{Pulley}}}{2}\right)} g \end{aligned} \nonumber$$

Підстановка в цифрах дає $$\frac{d V_{A}}{dt} = \frac{\left(m_{B}-m_{A}\right)}{\left(m_{A} + m_{B} + \frac{m_{\text {Pulley}}}{2}\right)} g = \frac{(60-30)}{\left(30+60+\dfrac{10}{2}\right)} g = \left(\frac{30}{95}\right) g = 3.098 \ \frac{\mathrm{m}}{\mathrm{s}^{2}} \nonumber$$

Таким чином циліндр$A$ розганяється вгору, а циліндр$B$ розганяється вниз зі швидкістю$3.098 \mathrm{~m} / \mathrm{s}^{2}$.

Коментар:

Визначте помилку, якби ми знехтували масою шківа: тобто яким було б прискорення, якби ми знехтували масою шківа?