6.1: Чому ця річ обертається?

Last updated
Save as PDF

Page ID: 34319

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Той, хто поміняв спущену шину, користувався гайковим ключем, кинув фрісбі, повісив на кінцівку дерева або штовхнув велику коробку, щось знає про схильність предметів обертатися або чинити опір обертанню. Кутовий момент - це велике фізичне властивість, пов'язане з цим явищем. Перш ніж ми зможемо розробити збереження співвідношення моменту моменту, ми повинні ввести кілька понять для опису кутового руху та моменту сили.

Розглянемо:

Яка мета бруска «шахраїв», застосована до гайкового ключа? (Брусок «шахраїв» - це шматок труби, прослизаний над кінцем гайкового ключа, щоб продовжити його довжину.)

Де найкраще натискати картотечну шафу на роликах? Як ви найкраще оцінювали?

Щоб освіжити пам'ять, уявіть, що у вашого автомобіля спущена шина і ви повинні її змінити (див. Малюнок\(\PageIndex{1}\)). Щоб змінити шину, спочатку піднімаєте шину від землі за допомогою автомобільного домкрата. Далі ви поміщаєте шинний праска на гайку з наконечником і намагаєтеся послабити її. На ескізі сила\(\mathbf{F}\) діє на шинне залізо в точці\(P\), вісь шини знаходиться в точці\(O\), а гайка розташована в точці\(N\).

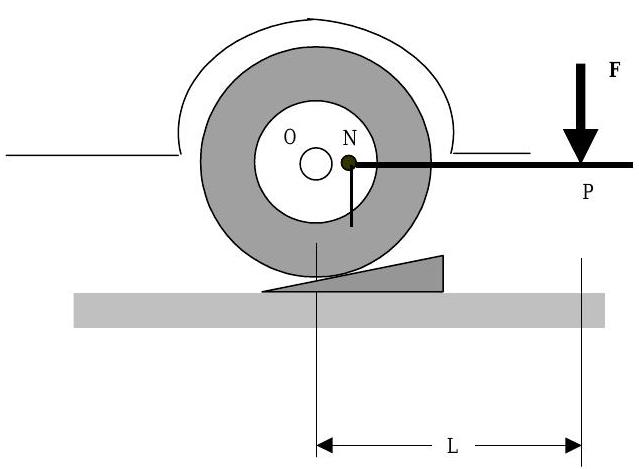
Шину утримують трохи від землі клином. Наконечник N на шині послаблюється шинним праскою, який тримається паралельно землі. На вільний кінець шинного заліза прикладається вниз сила F, в точці Р, розташованої на відстані L від центру шини.

Малюнок\(\PageIndex{1}\): Зміна шини.

Якщо вам пощастило в житті, ви можете бути новачком у зміні шин, і виявите, що шина обертається, коли ви натискаєте на залізо шини. Водій з меншою удачею та більшим досвідом зміни шин може лише частково підняти шину або вставити клин, щоб запобігти обертанню шини. Досвідчені шиномонтажники знають, що наша здатність послабити гайку залежить як від сили, так\(\mathbf{F}\) і від точки її застосування (точки\(P\)). Вони також знають, що ефективність прикладеного зусилля\(\mathbf{F}\) менше, якщо вона прикладена під кутом до шинного заліза.

Що буде, якби сила була застосована в точці\(N\)? Чи змогли б ви послабити горіх? Чи крутилася б шина?

6.1.1 Момент сили близько точки

Щоб кількісно оцінити здатність сили обертати шину, нам потрібна фізична величина, яка враховує величину та напрямок сили, а\(\mathbf{F}\) також точку її застосування. Кількість, яку ми бажаємо, - це момент сили про точку.

Момент сили\(\mathbf{F}\) навколо точки\(\bf{O}\) - векторний (або перехресний) добуток вектора положення\(\mathbf{r}\) і сили\(\mathbf{F}\):

\[ \mathbf{M}_O = \mathbf{r} \times \mathbf{F} \nonumber \]

де\(\mathbf{r}\) - вектор положення, що простягається від точки\(O\) до точки прикладання сили (див. Рис.\(\PageIndex{2}\)).

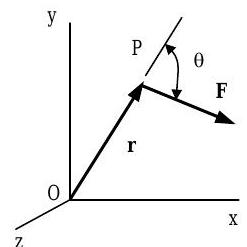
Тривимірна система координат з осями x, y та z містить точку P, розташування якої відносно початку O задається вектором r. Сила, представлена у вигляді вектора F, прикладається до точки P. Менший з двох кутів, зроблених лінією дії F з r, задається тета.

Малюнок\(\PageIndex{2}\): Обчислення моменту сили\(\mathbf{F}\) навколо точки\(O\).

Коли вектор положення\(\mathbf{r}\) і вектор сили\(\mathbf{F}\) записуються в терміні їх складових як\[\mathbf{r} = x \mathbf{i}+y \mathbf{j}+z \mathbf{k} \quad \text { and } \quad \mathbf{F}=F_{x} \mathbf{i}+F_{y} \mathbf{j}+F_{z} \mathbf{k} \nonumber \] Eq. \((\PageIndex{1})\)оцінюється наступним чином за допомогою стандартних крос-продуктових операцій:\[\begin{align} \mathbf{M}_{o} &=\mathbf{r} \times \mathbf{F}=\left| \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x & y & z \\ F_{x} & F_{y} & F_{z} \end{array}\right| \nonumber \\[4pt] &=\mathbf{i}\left|\begin{array}{cc} y & z \\ F_{y} & F_{z} \end{array}\right|-\mathbf{j}\left|\begin{array}{cc} x & z \\ F_{x} & F_{z} \end{array}\right|+\mathbf{k}\left|\begin{array}{cc} x & y \\[4pt] F_{x} & F_{y} \end{array}\right| \\ &=\left(y F_{z}-z F_{y}\right) \mathbf{i}-\left(x F_{z}-z F_{x}\right) \mathbf{j}+\left(x F_{y}-y F_{x}\right) \mathbf{k} \nonumber \end{align} \nonumber \]

Якщо обмежитися рухом у\(x \text{-} y\) площині (рух площини), єдиною складовою\(\mathbf{M}_O\) з ненульовим значенням є\(z\) -компонент — останній член з правого боку Eq. \((\PageIndex{3})\).

З нашого знання векторів можна сказати кілька речей про цей результат:

Вектор положення\(\mathbf{r}\) і вектор сили\(\mathbf{F}\) лежать в площині.
Момент\(\mathbf{M}_O\) сили\(\mathbf{F}\) навколо точки\(O\) є вектором (див. Ур. \((\PageIndex{3})\)).
Лінія дії вектора\(\mathbf{M}_{O}\) моменту нормальна (перпендикулярна) площині, яка містить обидва\(\mathbf{r}\) і\(\mathbf{F}\).
Точка застосування вектора моменту\(\mathbf{M}_{O}\) знаходиться в точці\(O\), точці, про яку ми приймаємо момент.
Почуття напрямку моменту\(\mathbf{M}_{O}\) і почуття обертання, яке воно могло б надати, можна описати правилом правої руки кількома способами (див. Малюнок\(\PageIndex{3}\)):

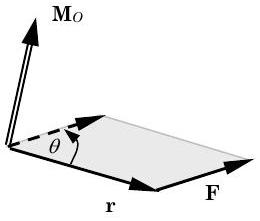
Малюнок\(\PageIndex{3}\): Відчуття напрямку\(\mathbf{M}_O\) використання правилом правої руки.
- Вирівняйте пальці правої руки в напрямку вектора положення\(\mathbf{r}\) і скрутіть їх у напрямку сили\(\mathbf{F}\). Великий палець тепер вказує у напрямку моменту,\(\mathbf{M}_{O}\) а пальці скручуються, щоб показати почуття обертання на даний момент\(\mathbf{M}_{O}\).
- Уявіть ковзання вектора\(\mathbf{r}\) або\(\mathbf{F}\) поки вони не будуть хвостиком до хвоста. Вирівняйте пальці правої руки в напрямку вектора положення\(\mathbf{r}\) і скрутіть пальці у напрямку сили\(\mathbf{F}\). Ваші згорнуті пальці тепер вказують на почуття обертання на даний момент,\(\mathbf{M}_{O}\) а великий палець вказує у напрямку моменту\(\mathbf{M}_{\text {O}}\).
- Скрутіть пальці правої руки і наведіть великий палець правої руки в напрямку моменту\(\mathbf{M}_{O}\). Напрямок, в якому скручуються пальці, - це почуття обертання на даний момент\(\mathbf{M}_{O}\).
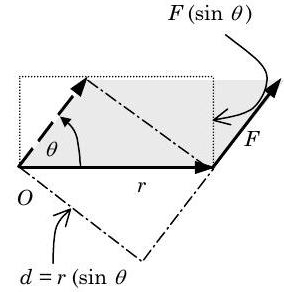
Величина вектора моменту\(\mathbf{M}_{O}\) є квадратним коренем точкового добутку\(\mathbf{M}_{O}\) з собою і розраховується наступним чином:\[\begin{array} M M_{O} &=\left|\mathbf{M}_{o}\right|=\left(\mathbf{M}_{O} \cdot \mathbf{M}_{O}\right)^{1 / 2} \\ &=\left[\left(y F_{z}-z F_{y}\right)^{2}+\left(x F_{z}-z F_{x}\right)^{2}+\left(x F_{y}-y F_{x}\right)^{2}\right]^{1 / 2} \end{array} \nonumber \] Його також можна обчислити за допомогою співвідношення,\[M_{o}=\left|\mathbf{M}_{o}\right|=|\mathbf{r}||\mathbf{F}| \sin \theta=r F(\sin \theta) \nonumber \] де\(\theta\) кут між лініями дії векторів\(\mathbf{r}\) і\(\mathbf{F}\) і вимірюється як би\(\mathbf{r}\) і\(\mathbf{F}\) були поміщені хвіст до хвоста. Позитивний кут задовольняє правилу праворуч, як описано вище. Еквалайзер. \(( \PageIndex{5})\)можна інтерпретувати як площу паралелограма, утвореного векторами\(\mathbf{r}\) і\(\mathbf{F}\) (Див. Рис.\(\PageIndex{4}\)).
Малюнок\(\PageIndex{4}\): Інтерпретація величини\(\mathbf{M}_O\) як площі.

Два додаткових прямокутника, показані на малюнку,\(\PageIndex{4}\) мають ділянки, рівні за величиною затіненої області. Прямокутник довжини\(d_{\perp}\) та ширини\(F\) має площу Прямокутник довжини\(r\) та ширини\(F \sin \theta\) має площу\[\begin{align} M_{O} &=r(F \sin \theta) \nonumber \\ &=r \times F_{\perp}=\left[\begin{array}{c} \text { Magnitude } \\ \text { of the } \\ \text { position vector } \mathbf{r} \end{array}\right] \times\left[\begin{array}{c} \text { Component of force } \mathbf{F} \\ \text { that is } \perp \text { to } \\ \text { the line-of-action of } \mathbf{r} \end{array}\right] \end{align} \nonumber \] Для більшості випадків з двовимірним (площинним) рухом ви побачите, що за допомогою Eqs.\[\begin{align} M_{O} &=(r \sin \theta) F \nonumber \\ &=d_{\perp} \times F \quad=\underbrace{\left[\begin{array}{c} \text { Shortest distance } \\ \text { between point } O \\ \text { and the line-of-action } \\ \text { of force } \mathbf{F} \end{array}\right]}_{\text {Often called the "lever arm" }} \times\left[\begin{array}{c} \text { Magnitude } \\ \text { of } \\ \text { force } \mathbf{F} \end{array}\right] \end{align} \nonumber \] \((\PageIndex{6})\)або набагато\((\PageIndex{7})\) простіше, ніж використання формальної математики крос-продукту.

Перевірте своє розуміння

Для кожного з наступних двовимірних випадків визначте величину і напрямок [За годинниковою стрілкою (CW) або проти годинникової стрілки (CCW)] моменту сили\(\mathbf{F}\) близько точки\(O\):

а)

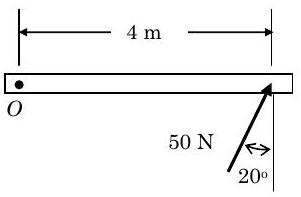
Горизонтальна смуга довжиною 4 метри має точку O на лівому кінці. На правому кінці планки прикладається сила 50 Н, спрямована вгору і вправо, в 20 градусах від вертикалі.

Малюнок\(\PageIndex{5}\): Зусилля прикладається під кутом до одного кінця бруса.

б)

Горизонтальна 4-метрова смуга має точку O в лівій кінцевій точці. До правого кінця планки прикладається сила 50 Н, спрямована вниз і вліво на 80 градусів від вертикалі.

Малюнок\(\PageIndex{6}\): Зусилля прикладається під кутом до одного кінця бруса.

в)

Об'єкт складається з двох горизонтальних смуг, правий кінець верхньої планки з'єднаний з лівим кінцем нижньої планки. Точка О - крайня ліва точка збірки. Сила 50 Н, спрямована вгору і вправо на 45 градусів від вертикалі, прикладається до точки 4 метри вправо і на 1 метр нижче О.

Малюнок\(\PageIndex{7}\): Зусилля прикладається під кутом до одного кінця жорсткого тіла.

Відповідь

а)\(187.9 \ \mathrm{N} \cdot \mathrm{m CCW}\)

б)\(34.73 \ \mathrm{N} \cdot \mathrm{m CW}\)

в)\(176.8 \ \mathrm{N} \cdot \mathrm{m CCW}\)

6.1.2 Момент сили пари

Існує особливий тип зовнішньої силової системи, яка називається силовою парою. Пара сил складається з двох зовнішніх сил, які мають однакову величину, паралельні лінії дії та протилежний сенс (див. Рис.\(\PageIndex{8}\)). Таким чином, пара сил призводить до нульової чистої сили на системі. Або заявивши про це іншим способом, пара сил передає нульовий лінійний імпульс системі. Однак швидке вивчення малюнка показує, що пара сил насправді намагається повернути або повернути систему.

Нерегулярно вигнуте тіло містить три точки O, O 'і O». Вектор сили F1 являє собою силу, прикладену до певної точки тіла, з величиною F. Вектор сили F2 являє собою силу, прикладену до якоїсь іншої точки тіла, також величини F і вздовж тієї ж лінії дії, що і F1, вказуючи в протилежному напрямку. Відстань між лініями дії сил задається d.

Малюнок\(\PageIndex{8}\): Сила пара.

Момент пари сили близько точки\(O\) можна обчислити з посиланням на малюнок\(\PageIndex{8}\) наступним чином:\[ \begin{align} \mathbf{M}_{O, \text { couple }} &= \mathbf{M}_{O, \ F_{1}} + \mathbf{M}_{O, \ F_{2}} \nonumber \\ &= \left( \mathbf{r}_{1} \times \mathbf{F}_{1} \right) + \left( \mathbf{r}_{2} \times \mathbf{F}_{2}\right) \quad\quad\quad \text { where } \left| \mathbf{F}_{1} \right| = \left|\mathbf{F}_{2}\right| = F \nonumber \\ &= \left[ \left( d_{\perp, 1} \times F_{1}\right) \,\, \mathrm{CCW} \right] + \left[ \left( d_{\perp, 2} \times F_{2}\right) \,\, \mathrm{CW} \right] \\ & = \left[ -\left( d_{\perp, 1} \times F_{1}\right) \quad + \quad \left(d_{\perp, 2} \times F_{2}\right) \right] \quad \text { CW } \nonumber \\ &= d \times F \quad \text { CW } \quad\quad\quad\quad\quad\quad\quad \text { where } d=\left| d_{\perp, 1}-d_{\perp, 2}\right| \nonumber \\ {} \nonumber \\ \mathbf{M}_{O, \text { couple }} &= d \times F \text{ in a CW direction} \nonumber \end{align} \nonumber \]

Зверніть увагу, що якби ми обчислили момент пари сили, показаної на малюнку\(\PageIndex{8}\) про точку\(O'\) або точку,\(O''\) ми б знайшли точно такий же результат. Таким чином, момент пари, здається, не прив'язаний до певної точки, на відміну від того, що ми знайшли з моментом сили про точку.

Можна сказати наступне про пару сили з силою\(\mathbf{F}\) і відстань,\(d\) що розділяє лінії дії сил:

Лінії дії двох сил в парі сили лежать в одній площині.
Пара сил не передає чистий лінійний імпульс до системи.
Момент, вироблений парою сили, є вектором\(\mathbf{M}_{\text {couple}}\).
Лінія дії вектора\(\mathbf{M}_{\text {couple}}\) моменту нормальна (перпендикулярна) площині, яка містить пару сил.
Точка застосування вектора моменту\(\mathbf{M}_{\text {couple}}\) може перебувати в будь-якій точці площини пари. Оскільки точка застосування вільна для переміщення, цей тип вектора іноді називають вільним вектором.
Відчуття вектора моменту,\(\mathbf{M}_{\text {couple can be obtained from ob. }}\) який обслуговує напрямок обертання, яку могла б надати пара сил. Напрямок вектора моменту можна знайти, завивши пальці правої руки, щоб відповідати почуттю пари сили і вирівнявши великий палець по лінії дії. Ваш великий палець тепер вказує в напрямку для вектора моменту\(\mathbf{M}_{\text {couple. }}\).
Величина вектора моменту\(\mathbf{M}_{\text {couple is equal to the product }}\) величини одного з векторів сили і найкоротша відстань між лініями дії,\(d\):\[M_{\text {couple}} = \left| \mathbf{M}_{\text {couple}}\right| = d \times |\mathbf{F}| = d \times F \nonumber \]

Ми часто стикаємося з системами, де розподіл сили на деякій частині кордону виглядає так, як показано в частині (а) малюнка\(\PageIndex{9}\). На верхній половині кордону сили стискають (тиснуть на систему), а на нижній половині кордону сили розтягують (тягнуть на систему). Якщо кожна сила на верхній половині має дзеркальне відображення протилежного сенсу на нижній половині, цей розподіл представляє пару, а чиста сила на кордоні дорівнює нулю; однак існує чистий момент через пару, як показано в частині (b) малюнка\(\PageIndex{9}\). Будуть також випадки, коли розподіл сили на кордоні насправді є сумою пари та чистої сили.

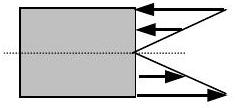Блок відчуває розподілену пару з правого боку. Для верхньої половини блоку розподілена сила спрямована вліво, а для нижньої - розподілена сила, розподілена симетрично до верху, спрямована вправо. — Малюнок\(\PageIndex{9}\): Момент розподіленої пари.

Блок з частини А фігури має свою розподілену пару, замінену єдиною вигнутою стрілкою, що представляє еквівалентний момент. — Малюнок\(\PageIndex{9}\): Момент розподіленої пари.

Перевірте своє розуміння

Обчисліть величину і напрямок (CW або CCW) для чистого моменту близько точки\(O\):

Точка О розташована на тілі неправильної форми. 4 фути вище О, 100 фунтів сили прикладається вправо. 4 фути праворуч від O, 50-фунт-сила прикладається вгору. Деяка відстань праворуч від O, пара сил з величиною 75 lbf і відстанню 2 футів, що розділяють сили, прикладається до тіла.

Малюнок\(\PageIndex{10}\): Точкові сили і пара сил прикладені до вигнутої форми.