3.5: Облік хімічних видів

Для багатьох проблем важливо стежити за окремими хімічними видами - атомами або молекулами. Приклади таких включають:

• процеси згоряння, наприклад спалювання бензину в повітрі
• процеси змішування, наприклад, змішування води та антифризу
• будь-який процес з хімічними реакціями
• приготування твердих розчинів, наприклад легованого кремнію кристала

Хоча загальна маса завжди зберігається, такого закону збереження не існує для хімічних видів загалом.

Експериментуючи зі збереженням маси

Щоб побачити, що відбувається, коли ми намагаємося врахувати окремі хімічні види, розглянемо стійкий хімічний реактор на рис\(\PageIndex{1}\). З'єднання\(A\) і з'єднання\(B\) надходять в реактор і об'єднують для отримання з'єднання\(C\).

Малюнок\(\PageIndex{1}\): Стаціонований хімічний реактор

Запис курсової форми збереження рівняння маси дає\[\frac{d m_{s y s}}{d t}=\dot{m}_1 + \dot{m}_2 - \dot{m}_3. \nonumber \] Для стаціонарної роботи швидкість зміни маси всередині системи дорівнює нулю. Перестановка і рішення для масової витрати на виході дає\[\dot{m}_3 = \dot{m}_1 + \dot{m}_2. \nonumber \] Тепер давайте спробуємо написати подібне рівняння для просто з'єднання\(C\). Починаючи зі збереження рівняння маси для тільки з'єднання,\(C\) ми маємо

\[ \underbrace{ \frac{dm_{C,sys}}{dt} }_{\begin{array}{c} \text {Rate of change} \\ \text {of compound } C \\ \text {inside the system} \end{array}} = \underbrace{ \dot{m}_{C, 1} + \dot{m}_{C, 2} }_{\begin{array}{c} \text {Mass flow rate} \\ \text {of compound } C \\ \text {entering the system} \end{array}} - \underbrace{ \dot{m}_{C, 3} }_{\begin{array}{c} \text {Mass flow rate} \\ \text {of compound } C \\ \text {leaving the system} \end{array}} \nonumber \]

За визначенням, для сталої системи інтенсивні та екстенсивні властивості системи не залежать від часу. Таким чином, термін швидкості зміни повинен дорівнювати нулю. Ми також знаємо з нашої постановки завдання, що тільки з'єднання\(A\) і\(B\) надходять в систему; таким чином, масові витрати\(C\) на входах 1 і 2 однаково нульові. Складання цього дає наступний результат:\[0=0 + 0 - \dot{m}_{C, 3} \nonumber \] Цей результат не відповідає нашому розумінню фізичної ситуації. Ми знаємо,\(C\) що з'єднання покидає наш сталий реактор. Звідки вона береться? Кілька моментів роздумів можуть припустити, що наш досвід говорить нам, що з'єднання\(C\) генерується всередині системи.

Якби ми спробували написати подібні рівняння для\(B\) складеного\(A\) та складного, ми б придумали той самий фізично непослідовний результат. У цьому випадку можна зробити висновок, що сполука\(A\) і з'єднання\(B\) споживаються всередині цієї системи.

Щоб виправити цю невідповідність, спробуємо змінити наш баланс маси, щоб врахувати генерацію та споживання окремих хімічних видів. Для нашого конкретного хімічного реактора рівняння може виглядати так для з'єднання\(i\):

\[\underbrace{ \frac{d m_{i, sys}}{d t} }_{\begin{array}{c} \text {Rate of accumulation} \\ \text {of compound } i \\ \text {inside the system} \end{array}} = \underbrace{ \dot{m}_{i, 1} + \dot{m}_{i, 2} - \dot{m}_{i, 3}} _ {\begin{array}{c} \text {Transport rate of} \\ \text {compound } i \\ \text {across the} \\ \text {system boundary} \end{array}} + \underbrace{ \dot{m}_{i, \text { gen}}} _ {\begin{array}{c} \text {Generation rate} \\ \text {of compound } i \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{i, \text { cons}}} _ {\begin{array}{c} \text {Consumption rate} \\ \text {of compound } i \\ \text {inside the system} \end{array}} \nonumber \]

Написання цього рівняння для кожного з трьох сполук у нашому хімічному реакторі з урахуванням відповідних припущень, наприклад, стаціонарної роботи та чистих сполук на трьох границях потоку, дає

\[\begin{array}{ll} \text { Compound } A: & 0=\dot{m}_{A, 1} - 0 + 0 - \dot{m}_{A, \text { cons }} \\ \text { Compound } B: & 0=\dot{m}_{B, 1} - 0 + 0 - \dot{m}_{B, \text { cons }} \\ \text { Compound } C: & 0=0-\dot{m}_{C, 3} + \dot{m}_{C, \text{ gen}} - 0 \end{array} \nonumber \]

Якщо підсумувати ці три рівняння, то отримаємо наступне співвідношення:\[0 = \underbrace{ \left[ \dot{m}_{A, 1} + \dot{m}_{B, 2} - \dot{m}_{C, 3} \right] }_{ =0 \atop \begin{array}{c} \text {From conservation} \\ \text {of total mass} \end{array}} + \left[ \dot{m}_{C, \text{ gen}} - \dot{m}_{A, \text { cons}}-\dot{m}_{B, \text { cons}} \right] \nonumber \] Оскільки члени в перших дужках з правого боку задовольняють збереженню рівняння загальної маси, записаного раніше, нам залишається висновок, що члени в другому наборі дужок повинні задовольняти наступним відносини:

\[ \underbrace{ \dot{m}_{C, \text{ gen}} }_{\begin{array}{c} \text {Generation rate} \\ \text {of compound } C \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{A, \text{ cons}} }_{\begin{array}{c} \text {Consumption rate} \\ \text {of compound } A \\ \text {inside the system} \end{array}} - \underbrace{ \dot{m}_{B, \text{ cons}} }_{\begin{array}{c} \text {Consumption rate} \\ \text {of compound } B \\ \text {inside the system} \end{array}} = 0 \nonumber \]

Досліджуючи цей результат, здавалося б, цей зв'язок є прямим наслідком емпіричного факту того, що загальна маса зберігається. У наступному розділі ми напишемо загальну бухгалтерську відомість для будь-якого хімічного виду з точки зору як видової маси, так і кількості кротів виду.

Рівняння обліку хімічних видів

Спираючись на результати останнього розділу та наш досвід роботи з системою бухгалтерського обліку, ми можемо написати два різних рівняння обліку або балансу для будь-якого окремого хімічного виду.

Масова основа для з'єднання\(i\)

На масовій основі рівняння обліку записується через масу системи, масові витрати, а також генерацію і витрату маси зазначеного з'єднання:

\[\underbrace{ \frac{d m_{i, sys}}{d t} }_{\begin{array}{c} \text {Rate of accumulation} \\ \text { of mass } \\ \text {of Compound } i \\ \text {inside the system} \end{array}} = \underbrace{ \left[ \sum_{in} \dot{m}_{i, i} - \sum_{out} \dot{m}_{i, e} \right] }_{\begin{array}{c} \text {Net flow rate} \\ \text {of mass} \\ \text {of Compound } i \\ \text {into the system} \end{array}} + \underbrace{ \left[ \dot{m}_{i, gen} - \dot{m}_{i, cons} \right] }_{\begin{array}{c} \text {Net generation rate} \\ \text {of mass} \\ \text{of Compound } i \\ \text {inside the system} \end{array}} \nonumber \]де\[\begin{aligned} m_{i, sys} &= \int_{V_{sys}} \rho_{i} \ dV, \text {the mass of } i \text{ inside the system }(\mathrm{kg}) \\ \dot{m}_{i, i} ; \, \dot{m}_{i, e} &=\text {mass flow rate of } i \text{ into or out of the system }(\mathrm{kg} / \mathrm{s}) \\ \dot{m}_{i, gen} ; \, \dot{m}_{i, cons} &=\text {generation/consumption rate of } i \text{ inside the system }(\mathrm{kg} / \mathrm{s}) \end{aligned} \nonumber \]

Зверніть увагу, що терміни генерації та споживання однаково нульові, якщо в системі не відбуваються хімічні реакції.

Молярна основа для з'єднання\(i\)

На молярній основі рівняння обліку записується через системні молі, молярні витрати, а також генерації та споживання молів зазначеної сполуки:\[\underbrace{ \frac{d n_{i, sys}}{dt} }_{\begin{array}{c} \text {Rate of Accumulation} \\ \text {of moles} \\ \text {of Compound } i \\ \text {inside the system} \end{array}} = \underbrace{\left[ \sum_{in} \dot{n}_{i, i} - \sum_{out} \dot{n}_{i, e} \right] }_{\begin{array}{c} \text {Net molar flow rate} \\ \text {of Compound } i \\ \text {into the system} \end{array}} + \underbrace{ \left[ \dot{n}_{i, gen} - \dot{n}_{i, cons} \right] }_{\begin{array}{c} \text {Net generation rate} \\ \text {of moles} \\ \text {of Compound } i \\ \text {inside the system} \end{array}} \nonumber \] де\[\begin{aligned} n_{i, sys} &=\int_{V_{sys}} \bar{\rho}_{i} \ dV, \text { the number of moles of} i \text{ inside the system (kmol) } \\ \bar{\rho}_{i} &=\text {molar density of } i \left(\mathrm{kmol} / \mathrm{m}^{3}\right) \\ \dot{n}_{i, i} ; \, \dot{n}_{i, e}&=\text {molar flow rate of } i \text{ into or out of the system }(\mathrm{kmol} / \mathrm{s}) \\ \dot{n}_{i, gen} ; \, \dot{n}_{i, cons}&=\text {generation/consumption rate of moles of } i \text { inside the system } (\mathrm{kmol} / \mathrm{s}) \end{aligned} \nonumber \] Знову ж таки, як і у випадку з рівнянням основи маси, терміни генерації та споживання однаково дорівнюють нулю якщо в системі не відбуваються хімічні реакції.

Застосування обліку хімічних видів

Існує два широкі класи проблем, в яких важливий облік хімічних видів:

• Системи без хімічних реакцій, і
• Системи з хімічними реакціями.

Системи без хімічних реакцій

Якщо система не має хімічних реакцій, перше, що потрібно визнати, це те, що і норма генерації, і норми споживання для будь-якої сполуки однаково нульові.

• Якщо хімічний склад для системи також постійний (з часом) і рівномірний (у просторі), рівняння обліку видів дублюють збереження рівнянь маси і нічого не додають до нашого аналізу.
• Якщо хімічний склад також залежить від часу і неоднорідний, рівняння обліку видів можуть надати додаткову інформацію, яка доповнює збереження рівнянь маси. Приклади цього включають проблеми, пов'язані з змішуванням, розділенням та дистиляцією.

Застосовуючи як збереження маси, так і рівняння обліку видів, важливо визнати, скільки незалежних рівнянь можна записати для конкретної системи.

Для будь-якої нереактивної системи максимальна кількість незалежних рівнянь, які можна отримати, застосовуючи збереження загальної маси і обліку видів, дорівнює кількості незалежних видів, що беруть участь в процесі.

Перевірте себе

Спробуйте свої сили, вирішивши, скільки незалежних рівнянь можна записати для наступних сталих систем:

(а) Трійник в повітроводі

• \(\quad\)Повітряний впуск-1
• Вихід-2\(\quad\) повітря
• Вихід-3\(\quad\) повітря

(б) Процес поділу повітря

• Впускний 1\(\quad\) Повітря, що складається з\(79 \% \mathrm{~N}_{2}\) і\(21 \% \mathrm{O}_{2}\) (молярний аналіз)
• Розетка-2\(\quad\) Чистий\(\mathrm{O}_{2}\)
• Розетка-3\(\quad\) Чистий\(\mathrm{N}_{2}\)

(c) Зволожувач

• \(\quad\)Повітряний впуск-1
• Вхід-2\(\quad\) Водяна пара
• Випуск-3 Суміш\(\quad\) повітряно-водяної пари

(г) Змішувальна камера

• Вхід-1 Водяна пара\(\left(\mathrm{H}_{2} \mathrm{O}\right)\)
• Впуск-2\(\quad\) Вуглекислий газ\(\left(\mathrm{CO}_{2}\right)\)
• Впускний 3 Повітря, що складається з\(79 \% \mathrm{~N}_{2}\) і\(21 \% \mathrm{O}_{2}\) (молярний аналіз)
• Вихід-4 Газоподібна суміш\(\mathrm{H}_{2} \mathrm{O}, \, \mathrm{CO}_{2}, \, \mathrm{N}_{2}\),\) і\(\mathrm{O}_{2}\)

(е) Процес дистиляції

• Впуск-1:\(\quad\) Водно-спиртова суміш зі складом 1
• Розетка-2:\(\quad\) Водно-спиртова суміш зі складом 2
• Розетка-3:\(\quad\) Водно-спиртова суміш зі складом 3

Наступні два приклади демонструють, як використовувати рівняння обліку видів для вирішення проблем, які не передбачають хімічних реакцій.

Облік видів - проблеми без хімічної реакції

Проблеми зі зміною складу можна розділити на дві групи: системи з хімічною реакцією і системи без хімічної реакції. У центрі уваги цього підрозділу - системи без хімічної реакції.

Рівняння обліку видів

Для систем без хімічної реакції рівняння обліку видів можна записати без термінів генерації/споживання. З точки зору маси складової\(j\) рівняння обліку видів стає

\[\frac{d m_{j, sys}}{d t} = \sum_{in} \dot{m}_{j, i} - \sum_{out} \dot{m}_{j, e} + \cancel {\dot{m}_{j, gen}}^{=0} - \cancel {\dot{m}_{j, cons}}^{=0} \quad \rightarrow \quad \frac{d m_{j, sys}}{d t} = \sum_{in} \dot{m}_{j, i} - \sum_{out} \dot{m}_{j, e} \nonumber \]а в перерахунку на кількість речовини\(j\) (молі компонента\(j\)) рівняння обліку видів стає

\[\frac{d n_{j, sys}}{d t} = \sum_{in} \dot{n}_{j, i} - \sum_{out} \dot{n}_{j, e} + \cancel{\dot{n}_{j, gen}}^{=0} - \cancel{\dot{n}_{j, cons}}^{=0} \quad \rightarrow \quad \frac{d n_{j, sys}}{d t} = \sum_{in} \dot{n}_{j, i} - \sum_{out} \dot{n}_{j, e} \nonumber \]

Ці рівняння можуть бути записані для відстеження будь-якої хімічної складової при вивченні поведінки системи зі змінним складом і відсутністю хімічних реакцій. Приклади цього типу проблем включають фізичні процеси змішування, поділу та дистиляції.

З огляду на систему з\(N_{\text {comp}}\) хімічними сполуками, ви можете написати загальну кількість\(N_{\text {comp}}+1\) рівнянь, застосовуючи збереження загальної маси\(m\) і застосовуючи види обліку кожного з\(N_{\text {comp}}\) сполук. На жаль, тільки\(N_{\text {comp}}\) з цих рівнянь є незалежними. (Це означає, що будь-яке\(N_{\text {comp}}\) з наявних\(N_{\text {comp }}+1\) рівнянь вище може бути об'єднано простою алгеброю для відновлення рівняння, що залишилося.)

Рівняння складу

Склад суміші завжди можна описати в перерахунку на масові частки і мольні фракції. Для будь-якої системи для кожного потоку потоку може бути записано одне рівняння композиції, а для опису вмісту системи може бути записано додаткове рівняння складу. Для стаціонарної системи рівняння складу системи є непотрібним.

Розглянемо відкриту систему з трьома компонентами\(A,\)\(B\), і\(C\). Для кожного вхідного або вихідного потоку, скажімо, потоку 1, ми можемо пов'язати масову (або молярну) швидкість потоку кожного компонента із загальною швидкістю потоку на вході або виході, як показано нижче:\[\begin{array}{llll} \dot{m}_1 = \dot{m}_{A, 1} + \dot{m}_{B, 1} + \dot{m}_{C, 1} &= m f_{A, 1} \dot{m}_{1} + m f_{B, 1} \dot{m}_{1} + m f_{C, 1} \dot{m} & \rightarrow & 1=m f_{A, 1} + m f_{B, 1} + m f_{C, 1} \\ \dot{n}_1 = \dot{n}_{A, 1} + \dot{n}_{B, 1} + \dot{n}_{C, 1} &= n f_{A, 1} \dot{n}_{1} + n f_{B, 1} \dot{n}_{1} + n f_{C, 1} \dot{n}_{1} & \rightarrow & 1 = n f_{A, 1} + n f_{B, 1} + n f_{C, 1} \end{array} \nonumber \] Для вмісту системи маса або кількість речовини (молі) для кожного компонента можна записати, як показано нижче:

\[\begin{array} m_{sys} &= m_{A, sys} + m_{B, sys} + m_{C, sys} \\ &= m f_{A, sys} m_{sys} + m f_{B, sys} m_{sys} + m f_{C, sys} m_{sys} \quad \rightarrow \quad &1 = mf_{A, sys} + mf_{B, sys} + mf_{C, sys} \\ n_{sys} &= n_{A, sys} + n_{B, sys} + n_{C, sys} \\ &=n f_{A, sys} n_{sys} + n f_{B, sys} n_{sys} + n f_{C, sys} n_{sys} \quad \rightarrow \quad &1 = nf_{A, sys} + nf_{B, sys} + nf_{C, sys} \end{array} \nonumber \]

Приклад - Проблема змішування

Конкретний хімічний процес вимагає суміші метанолу, етанолу та води з масовою витратою\(200 \mathrm{~kg} / \mathrm{h}\). Потік продукту формується за допомогою двох потоків, кожен з яких містить лише два компоненти. Відомі відомості про витрати і склад для цієї стаціонованої задачі змішування наведені в таблиці.

Використовуючи інформацію в таблиці і будь-які додаткові припущення, визначте невідомі склади і витрати. [Примітка: Ніяких хімічних реакцій не відбувається.]

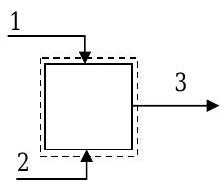
Малюнок\(\PageIndex{2}\): Налаштування системи для проблеми змішування.

Потік	Масова витрата	Склад — Маса%
		Метанол	Етанол	Вода
1			0
2	\(120 \mathrm{~kg} / \mathrm{h}\)	0
3	\(200 \mathrm{~kg} / \mathrm{h}\)	\(5.00\)	\(40.0\)

Аналіз:

Система\(\rightarrow\) Дивись картинку

Задача про\(\rightarrow\) швидкість періоду часу (нескінченно мала різниця в часі)

Матеріал для підрахунку\(\rightarrow\) Хімічні види і маса.

У цій задачі 6 невідомих: одна масова витрата і п'ять складів. Таким чином, нам потрібно 6 незалежних рівнянь, щоб зв'язати ці змінні, перш ніж ми зможемо вирішити задачу.

Застосовують збереження маси і видового обліку. Оскільки існує 3 сполуки, ми можемо отримати не більше 3 незалежних рівнянь шляхом написання обліку видів та збереження рівнянь маси для системи. Напишемо рівняння для загальної маси, етанолу і метанолу:

\[ \begin{align*} \text{Mass Balance:} \quad \cancel{ \frac{d m_{sys}}{dt} }^{=0, SS} &= \dot{m}_1 + \dot{m}_2 - \dot{m}_3 \\ 0 &= \dot{m}_1 + \dot{m}_2 - \dot{m}_3 \end{align*} \nonumber \]

\[\begin{align*} \text{Ethanol Balance:} \quad \frac{d m_{\text{eth, sys}}}{d t} &= \dot{m}_{\text{eth, 1}} + \dot{m}_{\text {eth, 2}} - \dot{m}_{\text {eth, 3}} = m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3} \\ 0 &= m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3} \end{align*} \nonumber \]

\[\begin{align*} \text{Methanol Balance:} \quad \frac{d m_{\text {meth, sys}}}{d t} &= \dot{m}_{\text {meth, 1}} + \dot{m}_{\text {meth, 2}} -\dot{m}_{\text {meth, 3}} = m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3} \\ 0 &= m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3} \end{align*} \nonumber \]

Оскільки ми використовували всі незалежні види обліку або рівняння балансу маси, ми повинні тепер перейти до співвідношення складу. Є три входи/виходи, і тому щонайбільше ми можемо написати 3 рівняння композиції, по одному для кожного потоку потоку:

\[ \begin{align*} \text{Stream 1:} & \quad 1=m f_{\text{meth, 1}} + m f_{\text{eth, 1}} + m f_{\text{w, 1}} \\ \text{Stream 2:} &\quad 1=mf_{\text{meth, 2}} + m f_{\text{eth, 2}} + m f_{\text{w, 2}} \\ \text{Stream 3:} &\quad 1=m f_{\text{meth, 3}} + m f_{\text{eth, 3}} + m f_{\text{w, 3}} \end{align*} \nonumber \]

Оскільки проблема знаходиться в сталому стані, немає необхідності в рівнянні складу, яке описує вміст системи.

Тепер у нас є шість рівнянь, які включають шість невідомих. Припускаючи, що рівняння незалежні, ми повинні мати можливість їх вирішувати для невідомих. Якщо підставити відому інформацію в шість рівнянь, ми маємо наступне:

\(0 = \dot{m}_1 + \dot{m}_2 - \dot{m}_3\)	\(\rightarrow\)	\(0 = \dot{m}_1 + \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right)\)
\(0 = m f_{\text {eth, 1}} \dot{m}_{1} + m f_{\text {eth, 2}} \dot{m}_{2} - m f_{\text {eth, 3}} \dot{m}_{3}\)	\(\rightarrow\)	\(0 = (0) \dot{m}_1 + m f_{\text{eth, 2}} \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - (0.40) \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right)\)
\(0 = m f_{\text {meth, 1}} \dot{m}_{1} + m f_{\text {meth, 2}} \dot{m}_{2} - m f_{\text {meth, 3}} \dot{m}_{3}\)	\(\rightarrow\)	\( 0 = m f_{\text{meth, 1}} + (0) \left( 120 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) - (0.05) \left( 200 \ \frac{\mathrm{kg}}{\mathrm{h}} \right) \)
\(1 = m f_{\text{meth, 1}} + m f_{\text{eth, 1}} + m f_{\text{w, 1}}\)	\(\rightarrow\)	\( 1 = m f_{\text{meth, 1}} + 0 + m f_{\text{w, 1}} \)
\(1 = m f_{\text{meth, 2}} + m f_{\text{eth, 2}} + m f_{\text{w, 2}}\)	\(\rightarrow\)	\( 1 = 0 + m f_{\text{eth, 2}} + m f_{\text{w, 2}} \)
\(1 = m f_{\text{meth, 3}} + m f_{\text{eth, 3}} + m f_{\text{w, 3}}\)	\(\rightarrow\)	\( 1 = 0.05 + 0.40 + m f_{\text{w, 3}} \)

Розв'язування цих рівнянь дає наступні відповіді:

Потік	Масова витрата	Склад — Маса%
		Метанол	Етанол	Вода
1	\( \mathbf{ 80 \ \mathrm{ \bf{kg}} / \mathrm{ \bf{h}} } \)	\(\bf{12.5}\)	\(0\)	\(\bf{87.5}\)
2	\( 120 \ \mathrm{kg} / \mathrm{h} \)	\(0\)	\(\bf{66.7}\)	\(\bf{33.3}\)
3	\(200 \ \mathrm{kg} / \mathrm{h} \)	\(5.00\)	\(40.0\)	\(\bf{55.0}\)

Це рішення можна зробити вручну; однак найкраще це зробити за допомогою системи комп'ютерної алгебри, як MAPLE, або числового розв'язувача, такого як EES.

Уроки, які слід витягти з цієї проблеми:

Загалом, для будь-якої проблеми з різним складом, але без хімічних реакцій,

• кожен потік потоку визначається, знаючи його масовий (або молярний) витрата і масові (або моль) частки компонентів в потоці.
• зміст кожної системи описується, знаючи масу (або родимки) і склад вмісту.
• для кожної системи (або підсистеми) можна записати одне рівняння композиції для кожного потоку потоку і одне рівняння композиції для вмісту системи. Всі ці рівняння є незалежними.
• для кожної системи (або підсистеми) в задачі можна записати стільки незалежних рівнянь обліку маси і/або видів, скільки в системі (або підсистемі) є хімічні сполуки (компоненти).

Для цього прикладу існує одна система з трьома потоками потоку і трьома з'єднаннями:

• Максимальна кількість змінних для опису композицій, маси та витрати:

\[(3 \text { mass flow rates})+(3 \text { flow streams})\left(3 \ \frac{\text {compounds}}{\text {flow stream}}\right)=12 \text { variables } \nonumber \]

• Максимальна кількість незалежних рівнянь, які можна записати, використовуючи склад, збереження маси та облік видів:

\[\underbrace{(1 \text { system})(3 \text { compounds})}_{\begin{array}{c} \text { Number of independent total mass} \\ \text {and/or species accounting equations} \end{array}} + \underbrace{(3 \text { flow streams})}_{\begin{array}{c} \text {Number of independent} \\ \text {composition equations} \end{array}}=6 \text { independent equations} \nonumber \]

• Число ступенів свободи - це різниця між кількістю змінних, необхідних для опису задачі, і кількістю незалежних рівнянь, які ви можете записати:

\[\underbrace{ \text{DOF}} _ {\begin{array}{c} \text {Degrees of} \\ \text {Freedom} \end{array}} = \underbrace{\text { NOV }}_{\begin{array}{c} \text {Number of} \\ \text {Variables} \end{array}} - \underbrace{\text {NOE}}_{\begin{array}{c} \text {Number of} \\ \text{Independent} \\ \text {Equations} \end{array}}= 12 - 6 = 6= \left[\begin{array}{c} \text {Minimum number of variables} \\ \text {that must be specified to obtain} \\ \text {a unique solution.} \end{array}\right] \nonumber \]

• Для цього прикладу постановка задачі надає інформацію про шість змінних. Без цієї інформації неможливо було б знайти унікальне рішення.
  Якби тільки п'ять змінних були присвоєні значення, можна було б вирішити лише для 6 інших змінних в терміні сьомої змінної. Наприклад, якщо масова швидкість потоку при 2 не була вказана, ви могли б розглядати її як незалежну змінну і вирішити для всіх інших невідомих змінних як функцію\(\dot{m}_{2}\). Для фізично можливого рішення\(\dot{m}_{2}\) може приймати лише обмежений діапазон значень, наприклад,\(0<\dot{m}_{2}<200 \mathrm{~kg} / \mathrm{h}\) тому що потік 2 є єдиним способом введення етанолу в змішувач.
  Якщо вказано лише п'ять змінних, унікальне рішення існувало б лише за умови надання додаткових обмежень на проблему. Вони можуть бути надані різними способами - шляхом визначення того, як деякі вхідні масові або видові потоки повинні бути розподілені в розетці, надаючи вам діапазон композицій для певних змінних і т.д. ці обмеження служать незалежними рівняннями, які можуть бути об'єднані з незалежними рівняннями розроблено на основі обліку складу та виду/маси. Потім цей набір може бути вирішений для невідомих змінних.
  Якщо більше шести змінних було присвоєно значення, не всі з них могли приймати довільні значення, щоб проблема мала рішення.

Приклад — Збагачення газової суміші

Газовий балон спочатку містить\(10 \ \mathrm{lbm}\) повітря. Бажано збагатити вміст кисню в суміші шляхом\(5 \ \mathrm{lbm}\) стравлювання повітря з балона з подальшим\(3 \ \mathrm{lbm}\) додаванням\(\mathrm{O}_{2}\). Визначте масу і молярний склад суміші після завершення процесу збагачення. Для цілей аналізу можна припустити, що повітря являє собою суміш\(23 \%\) кисню і\(77 \%\) азоту по масі.

Рішення

Відомо: Повітря стравлюється з газового балона і замінюється киснем.

Знайти: Склад (масові і мольні фракції) після процесу

Дано:

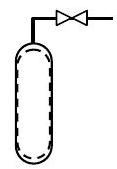
Малюнок\(\PageIndex{3}\): The system inside the tank.

\[ \begin{align*} \text{State 1:} \quad &m_{1}=10 \ \mathrm{lbm} \\ &m f_{\mathrm{O}_2}=0.23 ; \quad m f_{\mathrm{N}_2}=0.77 \end{align*} \nonumber \]

\[ \begin{align*} \text{Process 1} \rightarrow 2: \quad& \text{Remove } 5 \ \mathrm{lbm} \text{ air} \\ &\text{Add } 3 \ \mathrm{lbm} \text{ oxygen} \end{align*} \nonumber \]

Аналіз:

Стратегія\(\rightarrow\) Для пошуку композицій ми повинні знати загальну масу та масу кожного компонента в резервуарі в кінці процесу збагачення. Якщо ми зможемо знайти загальну масу і масу кожного компонента в кінцевому стані, ми можемо відповісти на це питання. Таким чином, припустимо, що у нас є три невідомих. Для їх вирішення ми застосуємо рівняння бухгалтерського обліку, оскільки ми хочемо пов'язати вміст системи в два різні часи.

\(\rightarrow\)Системи розглядають внутрішню частину бака як недеформуючу відкриту систему.

Властивість\(\rightarrow\) Маса і хімічні види

Період часу\(\rightarrow\) Оскільки лише інтерес до початкового та кінцевого станів, ймовірно, вимагає кінцевої форми часу

Написання збереження маси за будь-який час в процесі збагачення і подальша інтеграція за часовий проміжок збагачення дає:

\[\frac{d m_{sys}}{d t} = \dot{m}_{in} - \dot{m}_{out} \quad \rightarrow \quad \int\limits_{t_1}^{t_2} \left( \frac{d m_{sys}}{d t} \right) dt = \int_{t_1}^{t_2} \left( \dot{m}_{in} - \dot{m}_{out} \right) dt \quad \rightarrow \quad m_{sys, 2}-m_{sys, 1} = m_{in}-m_{out } \nonumber \]

Аналогічний вираз можна написати і для кожного хімічного виду в задачі:\[\begin{align*} \text{O}_{2}: \quad & \frac{d m_{sys, \text{O}_2}}{d t} = \dot{m}_{in, \ \text{O}_2} - \dot{m}_{out, \ \text{O}_2} & \rightarrow & m_{sys, \ \text{O}_2, \ 2} - m_{sys, \ \text{O}_2, \ 1} = m_{in, \ \text{O}_2} - m_{out, \ \text{O}_2} \\[4pt] \text{N}_{2}: \quad & \frac{d m_{sys, \ \text{N}_2}}{d t} = \dot{m}_{in, \ \text{N}_2} - \dot{m}_{out, \ \text{N}_2} & \rightarrow & m_{sys, \ \text{N}_2, \ 2} - m_{sys, \ \text{N}_2, \ 1} = m_{in, \ \text{N}_2} - m_{out, \ \text{N}_2} \end{align*} \nonumber \]

Це дає три рівняння; однак лише два з них є незалежними, тобто третє рівняння може бути утворено лінійною комбінацією двох інших рівнянь.

Для отримання третього незалежного рівняння розглянемо склад у стані 2. Це можна записати в одній з двох форм: З
\(\quad\) точки зору фактичної маси ми маємо\( \quad m_{sys, 2} = m_{sys, \text{O}_2, 2} + m_{sys, \text{N}_2, 2}\)
\(\quad\) В терміні масових часток, які ми маємо\(\quad 1=m f_{sys, \text{O}_2, 2} + m f_{sys, \text{N}_2, 2}\)

Як ви можете легко бачити, ці два рівняння не є незалежними, оскільки друге рівняння - це лише перше рівняння, розділене на масу системи.

Рішення для кінцевої маси\[m_{sys, \ 2}=m_{sys, \ 1} + m_{in} - m_{out} = (10+3-5) \ \mathrm{lbm} = 8 \ \mathrm{lbm} \nonumber \]

Тепер знайти кількість кисню і азоту в кінцевому стані

m_ {sys,\\ текст {N} _2,\ 2} - m_ {sys,\\ text {N} _2,\ 1} =\ скасувати {m_ {in,\\ text {N} _2}} ^ {=0} - m_ {out,\\ text {N} _2}

m_ {поза,\\ текст {N} _2} = m f_ {поза,\\ текст {N} _2}\ cdot m_ {out} = (0.77) (5\ текст {lbm}) = 3.85\\ текст {lbm}\ квадратний\ правий рядок\ квадратний m_ {sys,\\ текст {N} _2,\ 2} = (7.70 - 3.85)\\ текст {lbm} = 3,85\\ текст {lbm}

m_ {sys,\\ текст {N} _2,\ 1} = m f_ {sys,\\ текст {N} _2,\ 1}\ cdot m_ {sys,\ 1} = (0.77) (10\\ текст {lbm}) = 7.70\\ текст {lbm}

m_ {sys,\ 2} = m_ {sys,\\ текст {N} _2,\ 2} + m_ {sys,\\ text {O} _2,\ 2}\ квад\ стрілка вправо\ квад

Тепер, щоб знайти композиції, скористайтеся простою таблицею, як показано нижче:

	\(\frac{m_{j}}{\mathrm{lbm}}\)	\(m f_{j}\)	\(\frac{M_{j}}{(\mathrm{lbm} / \mathrm{lbmol})}\)	\(\frac{n_{j}}{\mathrm{lbmol}}\)	\(n f_{j}\)
\(\mathrm{O}_{2}\)	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(4.15\)	\ (m f_ {j}\) ">\(0.519\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(32.00\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.1297\)	\ (n f_ {j}\) ">\(0.485\)
\(\mathrm{N}_{2}\)	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(3.85\)	\ (m f_ {j}\) ">\(0.481\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(28.01\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.1375\)	\ (n f_ {j}\) ">\(0.515\)
	\ (\ frac {m_ {j}} {\ mathrm {lbm}}\) ">\(8.00\)	\ (m f_ {j}\) ">\(1.000\)	\ (\ frac {M_ {j}} {(\ mathrm {lbm}/\ mathrm {lbmol})}\) ">\(\ldots \ldots\)	\ (\ frac {n_ {j}} {\ mathrm {lbmol}}\) ">\(0.2672\)	\ (n f_ {j}\) ">\(1.000\)

Ваговий відсоток кисню збільшився від\(23 \%\) початкового до кінцевого значення\(51.9 \%\).

Коментар:

Зверніть увагу, що масові частки\((m f)\) і\((n f)\) мольні фракції неоднакові. Як зазначено нижче, масова частка вказує на склад в перерахунку на кількість маси кожного компонента, тоді як мольна частка враховує лише кількість молекул частинок. \

[\ begin {align*} m f &\ rightarrow\ frac {\ text {маса} j\ текст {молекули}} {\ текст {загальна маса молекул}}\ n f &\ rightarrow\ frac {\ text {кількість} j\ text {молекули}} {\ text {загальна кількість молекул}}\ end {align*}\ nonumber\]

Приклад - Безперервний процес флеш-дистиляції

Рідкий потік подачі безперервно подається в камеру флеш-дистиляції. У міру надходження рідини в камеру її тиск знижується і частина надходить рідини спалахує на пару. Струмінь рідких днищ зливають з підлоги камери і видаляють паровий дистилят поблизу верхньої частини камери.

Потік подачі складається з води, етанолу, метанолу, що надходять на 25\(\mathrm{lbm} / \mathrm{h}\)\(10 \mathrm{lbm} / \mathrm{h}\), і\(5 \mathrm{lbm} / \mathrm{h}\), відповідно. Нижній потік має масову витрату\(24 \mathrm{lbm} / \mathrm{h}\) і складається з\(83.3 \%\) води,\(12.5 \%\) етанолу та\(4.2 \%\) метанолу за вагою.

Визначте склад (масові і мольні фракції) і масову витрату дистиляту.

Рішення

Відомо: Умови експлуатації для камери безперервної флеш-дистиляції.

Знайти: Склад (масові і мольні фракції) і масова витрата дистиляту.

Дано:

Малюнок\(\PageIndex{4}\): Система всередині камери спалаху.

Потоки
\(1- \text{Feed}\)	\(\dot{m}_{\text {Water}}=25 \mathrm{lbm} / \mathrm{h}\) \(\dot{m}_{\text {Ethanol}}=10 \mathrm{lbm} / \mathrm{h}\) \(\dot{m}_{\text {Methanol}}=5 \mathrm{lbm} / \mathrm{h}\)
\(2- \text{Distillate}\)
\(3- \text{Bottoms}\)	\(m f_{\text {Water}}=83.3 \%\) \(m f_{\text {Ethanol}}=12.5 \%\) \(m f_{\text {Methanol}}=4.2 \%\) \(\dot{m}=24 \mathrm{lbm} / \mathrm{h}\)

Аналіз:

Стратегія\(\rightarrow\) Оскільки ми зацікавлені у співвідношенні вхідних потоків з виходом потоків, це здається кандидатом на збереження обліку маси та видів.

Система\(\rightarrow\) Недеформуюча, відкрита система, утворена об'ємом внутрішньої частини бака

Властивість:\(\rightarrow\) Маса і види, оскільки у нас є суміші, які змінюють склад

Період часу\(\rightarrow\) Оскільки система подається безперервно, припускайте сталий стан

Щоб повністю вказати всі входи та виходи такої проблеми, потрібно знати склад та загальну масову витрату на кожному вході/виході АБО масову витрату для кожного виду та загальну масову витрату на кожному вході/виході. Таким чином, загальна кількість невідомих

\[ \underbrace{ \left[ \left( \text{Number of Species} \right) + 1 \right] }_{mf_{j} \text{'s and } \dot{m}} \times \left[ \text{Number of inlets/outlets} \right] = \left[ 3 \times 1 \right] \times \left[ 3 \right] = \underbrace{ 12 \ \text{unknowns} }_{\begin{array}{c} mf_{\text{Water}}, \ mf_{\text{Ethanol}}, \ mf_{\text{Methanol}}, \ \dot{m} \\ \text {for feed, distillate, and bottoms} \end{array}} \nonumber \]

\[ \underbrace{ \left[ \left( \text{Number of Species} \right) + 1 \right] }_{mf_{j} \text{'s and } \dot{m}} \times \left[ \text{Number of inlets/outlets} \right] = \left[ 3 \times 1 \right] \times \left[ 3 \right] = \underbrace{12 \text{ unknowns} }_ {\begin{array}{c} \dot{m}_{\text{Water}}, \ \dot{m}_{\text{Ethanol}}, \ \dot{m}_{\text{Methanol}} \\ \text {for feed, distillate, and bottoms} \end{array}} \nonumber \]

Щоб допомогти візуалізувати те, що ми знаємо, а чого не знаємо, створимо таблицю:

	\(\dot{m}_{j} \ (\mathrm{lbm} / \mathrm{h}) \)	Склад
	\ (\ точка {m} _ {j}\ (\ матхрм {lbm}/\ матхрм {h})\) ">	\(\text{Water}\)	\(\text{Ethanol}\)	\(\text{Methanol}\)
\(1 - \text{Feed}\)	\ (\ точка {m} _ {j}\ (\ матхрм {lbm}/\ матхрм {h})\) ">\(\text{Eq. } 1\)	\(\text{Eq. } 2\)	\(\text{Eq. } 3\)	\(\text{Eq. } 4\)
\(2 - \text{Distillate}\)	\ (\ точка {m} _ {j}\ (\ матхрм {lbm}/\ матхрм {h})\) ">\(\text{Eq. } 5\)	\(\text{Eq. } 6\)	\(\text{Eq. } 7\)	\(\text{Eq. } 8\)
\(3 - \text{Bottoms}\)	\ (\ точка {m} _ {j}\ (\ матхрм {lbm}/\ матхрм {h})\) ">\(24.0\)	\(83.3\)	\(12.5\)	\(4.2\)

Спостерігаючи за таблицею, ми бачимо, що у нас вже є чотири частини інформації. Враховуючи масові витрати на потоці подачі, ми можемо знайти склад на потоці подачі, використовуючи співвідношення складу потоку корму.\((\text{Eq. }1)\)

\[ \text{Eq. }1 \quad \rightarrow \quad \dot{m}_1 = \dot{m}_{\text {Water}, \ 1} + \dot{m}_{\text {Ethanol}, \ 1} + \dot{m}_{\text {Methanol}, \ 2} = (25+10+5) \ \frac{\mathrm{lbm}}{\mathrm{h}} = 40 \ \frac{\mathrm{lbm}}{\mathrm{h}} \nonumber \]

Потім за допомогою визначення масових часток\((\text{Eq. } 2, \ 3,\) і\(4)\) для подачі потоку:

\[ \text{Eq. } 2, \ 3, \ 4 \quad \rightarrow \quad m f_{\text {Water}, \ 1} = \frac{\dot{m}_{\text {water}, \ 1}}{\dot{m}_1} = \frac{25}{40} = 62.5 \% \ ; \quad m f_{\text {Ethanol}, \ 1} = \frac{10}{40}=25.0 \% \ ; \quad m f_{\text {Methanol}, \ 1} = \frac{5}{40}=12.5 \% \nonumber \]

Зараз залишилося всього чотири невідомих. Загальна масова витрата може бути вирішена для запису збереження маси для системи\((\text{Eq. } 5)\)

\[ \text{Eq. } 5 \rightarrow \underbrace{ \cancel{ \frac{d m_{sys}}{dt} }^{=0} }_{\begin{array}{c} \text{steady-state} \\ \text{conditions} \end{array}} = \dot{m}_1 - \dot{m}_2 - \dot{m}_3 \quad \rightarrow \quad \dot{m}_2 = \dot{m}_1 - \dot{m}_3 = (40 - 24) \ \frac{\mathrm{lbm}}{\mathrm{h}} = 16 \ \frac{\mathrm{lbm}}{\mathrm{h}} \nonumber \]

Решта невідомі можна визначити, застосувавши рівняння обліку видів для води, етанолу та метанолу. Отримані рівняння виглядають так само, як\(\text{Eq. } 5\) за винятком того, що вони записані для кожного виду.

\[ \begin{align*} &\dot{m}_{\text {water}, \ 2} = \dot{m}_{\text {water}, \ 1} - \dot{m}_{\text {water}, \ 3} = \dot{m}_{\text {water}, \ 1} - m f_{\text {water}, \ 3} \dot{m}_3 = [25.0 - (0.833)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 5.01 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {water}, \ 2} = \frac{\dot{m}_{\text {water}, \ 2}}{\dot{m}_2} = \frac{5.01}{16.0} = 31.3 \% \end{align*} \nonumber \]

\[ \begin{align*} &\dot{m}_{\text {ethanol}, \ 2} = \dot{m}_{\text {ethanol}, \ 1} - \dot{m}_{\text {ethanol}, \ 3} = \dot{m}_{\text {ethanol}, \ 1} - m f_{\text {ethanol}, \ 3} \dot{m}_3 = [10.0-(0.125)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 7.00 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {ethanol}, \ 2} = \frac{\dot{m}_{\text {ethanol}, \ 2}}{\dot{m}_2} = \frac{7.00}{16.0}=43.7 \% \end{align*} \nonumber \]

\[ \begin{align*} &\dot{m}_{\text {methanol}, \ 2} = \dot{m}_{\text {methanol}, \ 1} - \dot{m}_{\text {methanol}, \ 3} = \dot{m}_{\text {methanol}, \ 1} - m f_{\text {methanol}, \ 3} \dot{m}_{3} = [5.0-(0.042)(24.0)] \ \frac{\mathrm{lbm}}{\mathrm{h}} = 3.99 \ \frac{\mathrm{lbm}}{\mathrm{h}} \\ &m f_{\text {methanol}, \ 2} = \frac{\dot{m}_{\text {methanol}, \ 2}}{\dot{m}_2} = \frac{3.99}{16.0} = 25.0 \% \end{align*} \nonumber \]

Молярний склад дистиляту можна обчислити після знаходження молярних швидкостей потоку:

	Масова витрата	Молярна маса	Молярна швидкість потоку	Моль фракція
\(\text{Water}\)	\(5.01 \ \mathrm{lbm} / \mathrm{h}\)	\(18.02 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.2780 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.409\)
\(\text{Ethanol}\)	\(7.00 \ \mathrm{lbm} / \mathrm{h}\)	\(46.07 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.1519 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.224\)
\(\text{Methanol}\)	\(3.99 \ \mathrm{lbm} / \mathrm{h}\)	\(32.05 \ \mathrm{lbm} / \mathrm{lbmol}\)	\(0.2494 \ \mathrm{lbmol} / \mathrm{h}\)	\(0.367\)
	\(16.00 \ \mathrm{lbm} / \mathrm{h}\)	\(\cdots\)	\(0.6793 \ \mathrm{lbmol} / \mathrm{h}\)	\(1.000\)

Системи з хімічними реакціями

Коли хімічні реакції відбуваються в системі, терміни споживання та генерації більше не кожен нуль. Щоб оцінити ці вирази, ви повинні спиратися на відповідні збалансовані хімічні рівняння, які застосовуються до задіяних реакцій. Через це молярна форма рівняння обліку видів є тією, яка зазвичай використовується при протіканні хімічних реакцій.

Знову ж таки, важливо точно визнати, скільки незалежних рівнянь можна отримати, застосовуючи облік збереження маси та видів.

Для реактивної системи кількість незалежних рівнянь, які можна отримати при збереженні маси і виду обліку дорівнює кількості незалежних видів плюс кількість незалежних хімічних реакцій. (Додаткові рівняння забезпечуються збалансованими хімічними рівняннями для кожної незалежної реакції.)

Додатки для систем з хімічними реакціями виходять за рамки цього тексту. Однак короткий приклад проілюструє, як отримують терміни генерації та споживання з хімічних рівнянь. Ці теми більш детально розглядаються на курсах хімічної інженерії. Останній приклад у цьому розділі демонструє, як можна підійти до проблеми з хімічними реакціями.

Приклад —Виготовлення\(\mathrm{CO}_2\)

Резервуар містить\(2 \ \mathrm{kmol}\) окис вуглецю\((\mathrm{CO})\) та\(2 \ \mathrm{kmol}\) кисень\(\left(\mathrm{O}_{2}\right)\). Якщо вихідна\(50 \%\) кількість\(\mathrm{CO}\) вступає в\(\mathrm{O}_{2}\) реакцію з формою\(\mathrm{CO}_{2}\), визначте кількість\(\mathrm{CO}, \mathrm{CO}_{2}\) і\(\mathrm{O}_{2}\) в кінцевій суміші.

Рішення

Відомо: Суміш\(\mathrm{CO}\) і\(\mathrm{O}_{2}\) вступає в реакцію в закритій системі.

Знайти: Кількість\(\mathrm{CO}, \mathrm{O}_{2}\), і\(\mathrm{CO}_{2}\) в суміші, якщо\(50 \%\) з\(\mathrm{CO}\) оригіналу реагує.

Дано:

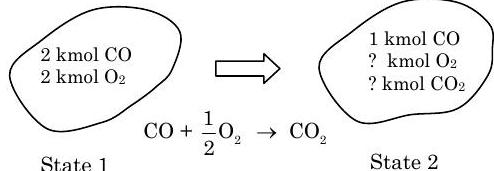
Малюнок\(\PageIndex{5}\): Стани 1 і 2 системи, і хімічна реакція, що відповідає за зміну станів.

Аналіз:

Стратегія\(\rightarrow\) Оскільки це передбачає суміші речовин і реакцій, використовуйте облік видів.

\(\rightarrow\)Систему розглядають замкнуту систему, яка включає всю масу спочатку в систему.

Властивість підраховувати\(\rightarrow\) Хімічні види

Період часу\(\rightarrow\) Оскільки зацікавлені в початковому та кінцевому стані, використовуйте форму скінченного часу.

Загалом, для кожного виду\(j\)

\[\frac{d n_{sys, j}}{d t} = \underbrace{ \cancel{ \sum_{in} \dot{n}_{j, i} - \sum_{out} n_{j, e} }^{=0} }_{\text {closed system}}+\dot{n}_{j, \ gen} - \dot{n}_{j, \ cons} \quad \rightarrow \quad \underbrace{ n_{j, 2} - n_{j, 1} }_{\begin{array}{c} \text{dropped the system} \\ \text{subscript} \end{array}} = n_{j, \ gen} - n_{j, \ cons} \nonumber \]

Тепер для кожного виду

\[ \begin{align*} & \text{CO:} \quad &\cancel{ n_{\text{CO}, \ 2} }^{=0} + \cancel{ n_{\text{CO}, \ 1} }^{=0} = \cancel{ n_{\text{CO}, \ gen} }^{=0} - n_{\text{CO}, \ cons} \quad &\rightarrow \quad\quad n_{\text{CO}, \ cons} = 1 \ \text{kmol} \\ & \text{O}_2: \quad &n_{\text{O}_2, \ 2} - \cancel{ n_{\text{O}_2, \ 1} }^{=0} = \cancel{ n_{\text{O}_2, \ gen} }^{=0} - n_{\text{O}_2, \ cons} \quad &\rightarrow \quad\quad n_{\text{O}_2, \ 2} = -n_{\text{O}_2, \ cons} \\ &\text{CO}_2: \quad &n_{\text{CO}_2, \ 2} - \cancel{ n_{\text{CO}_2, \ 1} }^{=0} = n_{\text{CO}_2, \ gen} - \cancel{ n_{\text{CO}_2, \ cons} }^{=0} \quad &\rightarrow \quad\quad n_{\text{CO}_2, \ 2} = n_{\text{CO}_2, \ gen} \end{align*} \nonumber \]

Це дає нам чотири невідомих і лише два рівняння. Щоб отримати інші рівняння, подивіться на рівняння хімічної реакції. З точки зору споживання і генерації хімічна реакція виглядає наступним чином:

\[\begin{gathered} n_{\text {CO}, \ cons} \mathrm{CO} + n_{\text{O}_2, \ cons} \mathrm{O}_2 \rightarrow n_{\text{CO}_2, \ gen} \mathrm{CO}_2 \\[4pt] \mathrm{CO} + \frac{n_{\text{O}_2, \ cons}}{n_{\text {CO}, \ cons}} \mathrm{O}_2 \rightarrow \frac{n_{\text{CO}_2, \ gen }}{n_{\text {CO}, \ cons }} \mathrm{CO}_2 \end{gathered} \nonumber \]

Якщо порівняти це рівняння з збалансованим хімічним рівнянням для реакції\(\mathrm{CO}\) з\(\mathrm{O}_2\) на форму\(\mathrm{CO}_2\), то можна визначити два залишилися рівняння між невідомими:

\[\begin{array}{c} \mathrm{CO} + \dfrac{n_{\text{O}_2, cons}}{n_{\text{CO}, \ cons}} \mathrm{O}_2 \rightarrow \dfrac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} \mathrm{CO}_{2} \\[4pt] \mathrm{CO} + \frac{1}{2} \mathrm{O}_2 \rightarrow \mathrm{CO}_2 \end{array} \quad \Rightarrow \quad \frac{n_{\text{O}_2, \ cons}}{n_{\text{CO}, \ cons}} = \frac{1}{2} \quad \& \quad \frac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} = 1 \nonumber \]

Таким чином, кінцеві склади виглядають наступним чином:\[\begin{align*} &n_{\text{CO}, \ 2} = 1 \ \mathrm{kmol} \\ &n_{\text{O}_2, \ 2} = n_{\text{O}_2, \ gen} = \frac{n_{\text{O}_2, \ gen}}{n_{\text{CO}, \ cons}} n_{\text{CO}, \ cons} = \left( \frac{1}{2} \right) (1 \ \mathrm{kmol}) = \frac{1}{2} \ \mathrm{kmol} \\[4pt] &n_{C\text{O}_2, \ 2} = n_{\text{CO}_2, \ gen} = \frac{n_{\text{CO}_2, \ gen}}{n_{\text{CO}, \ cons}} n_{\text{CO}, cons}=(1)(1 \ \mathrm{kmol}) = 1 \ \mathrm{kmol} \end{align*} \nonumber \]

Коментарі:

(1) Кінцева суміш\(3.5 \ \mathrm{kmol}\) порівняно з початковою сумішшю.\(4.0 \ \mathrm{kmol}\) Як правило, кроти не консервуються.

(2) Альтернативний підхід полягає у написанні рівнянь обліку видів для атомних видів,\(\text{C}\) і\(\text{O}\). Зверніть увагу, що атомні види, як і загальна маса, зберігаються.