Skip to main content
LibreTexts - Ukrayinska

7.1: Вступ

  1. Last updated
  2. Save as PDF
  • Page ID
    74987

    • Boundless
    • Boundless
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Лінійний імпульс

    Лінійний імпульс - добуток маси і швидкості об'єкта, він зберігається при пружних і непружних зіткненнях.

    навчальні цілі

    • Обчисліть імпульс двох стикаються об'єктів

    У класичній механіці лінійний імпульс, або просто імпульс (одиниця СІ кг м/с, або еквівалентно N с), є добутком маси і швидкості об'єкта. Математично він стверджується так:

    \[\mathrm{p=mv}\]

    (Зауважте, що p і v є векторами.) Як і швидкість, лінійний імпульс - це векторна величина, яка має напрямок, а також величину. Лінійний імпульс особливо важливий, оскільки це збережена величина, що означає, що в замкнутій системі (без будь-яких зовнішніх сил) її загальний лінійний імпульс не може змінюватися.

    Оскільки імпульс має напрямок, його можна використовувати для прогнозування результуючого напрямку об'єктів після їх зіткнення, а також їх швидкості. Імпульс зберігається як при непружних, так і в пружних зіткненнях. (Кінетична енергія не зберігається при непружних зіткненнях, але зберігається при пружних зіткненнях.) Важливо зазначити, що якщо зіткнення відбувається на поверхні з тертям, або якщо є опір повітря, нам потрібно буде враховувати імпульс тіл, які будуть перенесені на поверхню і/ або повітря.

    Давайте розглянемо простий, одновимірний приклад: Імпульс системи з двох частинок - це сума їх моментів. Якщо дві частинки мають маси m 1 і m 2, а швидкості v 1 і v 2, сумарний імпульс дорівнює:

    \[\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\]

    Майте на увазі, що імпульс і швидкість є векторами. Тому в 1D, якщо дві частинки рухаються в одному напрямку, v1 і v2 мають однаковий знак. Якщо частинки рухаються в протилежних напрямках, вони матимуть протилежні ознаки.

    Якби дві частинки рухалися на площині, ми б обрали нашу xy-площину, щоб бути на площині руху. Потім ми можемо записати x і y складові загального імпульсу як:

    \[\begin{align} \mathrm{p_x} & \mathrm{=p_{1x}+p_{2x}=m_1v_{1x}+m_2v_{2x}} \\ \mathrm{p_y} & \mathrm{=p_{1y}+p_{2y}=m_1v_{1y}+m_2v_{2y}.} \end{align}\]

    Якщо 2D вектор імпульсу розкладається на дві складові, рівняння для кожного компонента зводяться до його 1D еквівалентів.

    Імпульс, як і енергія, важливий, оскільки він зберігається. «Колиска Ньютона», показана в, є прикладом збереження імпульсу. Як ми будемо обговорювати в наступній концепції (про Momentum, Force і Другий закон Ньютона), в класичній механіці збереження лінійного імпульсу мається на увазі законами Ньютона. У природі зберігається лише кілька фізичних величин. Вивчення цих величин дає фундаментальне розуміння того, як працює природа.

    зображення

    Колиска Ньютона: Загальний імпульс системи (або колиски) зберігається. (Нехтуючи втратами на тертя в системі.)

    Імпульс, сила та другий закон Ньютона

    У найзагальнішому вигляді 2-й закон Ньютона можна записати як\(\mathrm{F=\frac{dp}{dt}}\).

    навчальні цілі

    • Пов'язати Другий закон Ньютона з імпульсом і силою

    У замкнутій системі (тій, яка не обмінюється ніякої матерії з зовнішнім і не діє на зовнішні сили) сумарний імпульс постійний. Цей факт, відомий як закон збереження імпульсу, мається на увазі закони руху Ньютона. Припустимо, наприклад, що дві частинки взаємодіють. Через третього закону сили між ними рівні і протилежні. Якщо частинки пронумеровані 1 і 2, другий закон стверджує, що

    \[\mathrm{\dfrac{dp_1}{dt}=−\dfrac{dp_2}{dt}}\]

    або

    \[\mathrm{\dfrac{d}{dt}(p_1+p_2)=0}\]

    Тому сумарний імпульс (р 1 + р 2) постійний. Якщо швидкості частинок складають u 1 і u 2 перед взаємодією, а після - v 1 і v 2, то

    \[\mathrm{m_1u_1+m_2u_2=m_1v_1+m_2v_2}\]

    Цей закон дотримується незалежно від характеру міжчастинкової (або внутрішньої) сили, якою б складною не була сила між частинками. Аналогічно, якщо частинок кілька, імпульс, що обмінюється між кожною парою частинок, додає до нуля, тому загальна зміна імпульсу дорівнює нулю.

    Другий закон Ньютона

    Ньютон фактично заявив про свій другий закон руху з точки зору імпульсу: Чиста зовнішня сила дорівнює зміні імпульсу системи, розділеної на час, протягом якого вона змінюється. Використовуючи символи, цей закон

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt},}\]

    де\(\mathrm{F_{net}}\) чиста зовнішня сила,\(\mathrm{Δp}\) - це зміна імпульсу, і\(\mathrm{Δt}\) це зміна часу.

    Це твердження другого закону руху Ньютона включає в себе більш\(\mathrm{F_{net}=ma}\( as a special case. We can derive this form as follows. First, note that the change in momentum \(\mathrm{Δp}\) звичний даний\(\mathrm{Δp=Δ(mv)}\). Якщо маса системи постійна, то\(\mathrm{Δ(mv)=mΔv}\). Таким чином, для постійної маси другий закон руху Ньютона стає

    \[\mathrm{F_{net}=\dfrac{Δp}{Δt}=\dfrac{mΔv}{Δt}.}\]

    Тому що\(\mathrm{\frac{Δv}{Δt}=a}\), ми отримуємо звичне рівняння,\(\mathrm{F_{net}=ma}\) коли маса системи постійна. Другий закон руху Ньютона, заявлений з точки зору імпульсу, є більш загальноприйнятим, оскільки він може застосовуватися до систем, де змінюється маса, таких як ракети, а також до систем постійної маси.

    зображення

    Імпульс у закритій системі: У грі в більярд систему цілих куль можна вважати закритою системою. Тому загальний імпульс куль зберігається.

    Імпульс

    Імпульс, або зміна імпульсу, дорівнює середній чистої зовнішньої сили, помноженої на час дії цієї сили.

    навчальні цілі

    • Поясніть взаємозв'язок між зміною імпульсу та кількістю часу дії сили

    Імпульс

    Сили виробляють або прискорення, або уповільнення на рухомих тілах, і чим більша сила, що діє на об'єкт, тим більша його зміна швидкості і, отже, більша його зміна імпульсу. Однак зміна імпульсу також пов'язана з тим, як довго діє сила. Якщо коротка сила прикладена до заглохлого автомобілю, виробляється зміна його імпульсу. Та ж сила, застосована протягом тривалого періоду часу, виробляє більшу зміну імпульсу автомобіля. Величина імпульсу - сила × часовий інтервал, або в скорочених позначеннях:

    Momentum & Impulse: Короткий огляд імпульсу та імпульсу для учнів фізики середньої школи.

    \[\mathrm{Impulse=FΔt,}\]

    де F - чиста сила на систему, а Δt - тривалість сили.

    З 2-го закону Ньютона:

    \[\mathrm{F = \dfrac{\Delta p}{\Delta t} \; (\Delta p: change \; in \; momentum),}\]

    зміна імпульсу дорівнює середньої чистої зовнішньої сили, помноженої на час дії цієї сили.

    \[\mathrm{Δp=FΔt.}\]

    Тому імпульс, як визначено в попередньому пункті, просто еквівалентний р.

    Сила, витримана протягом тривалого часу, виробляє більшу зміну імпульсу, ніж та сама сила, застосована коротко. Невелика сила, що застосовується протягом тривалого часу, може спричинити таку ж зміну імпульсу, як велика сила, прикладена коротко, оскільки це важливий продукт сили та час, протягом якого вона застосовується. Імпульс завжди дорівнює зміні імпульсу і вимірюється в Ns (секундах Ньютона), оскільки і сила, і часовий інтервал важливі при зміні імпульсу.

    Наше визначення імпульсу включає в себе припущення, що сила постійна протягом часового інтервалу\(\mathrm{Δt}\). Сили, як правило, не постійні. Сили значно змінюються навіть протягом розглянутих коротких часових інтервалів. Однак можна знайти середню ефективну силу,\(\mathrm{F_{eff}}\) яка дає той самий результат, що і відповідна сила, що змінюється в часі. показує графік того, як виглядає фактична сила як функція часу для кулі, що відскакує від підлоги. Площа під кривою має одиниці імпульсу і дорівнює імпульсу або зміні імпульсу між часом\(\mathrm{t_1}\) і\(\mathrm{t_2}\). Ця площа дорівнює площі всередині прямокутника, обмеженої\(\mathrm{F_{eff}, t_1,}\) і\(\mathrm{t_2}\). Таким чином, імпульси і їх вплив однакові як для реальних, так і для ефективних сил. Аналогічно, ми можемо просто знайти площу під кривою F (t) між\(\mathrm{t_1}\) і\(\mathrm{t_2}\) обчислити імпульс в математичній формі:

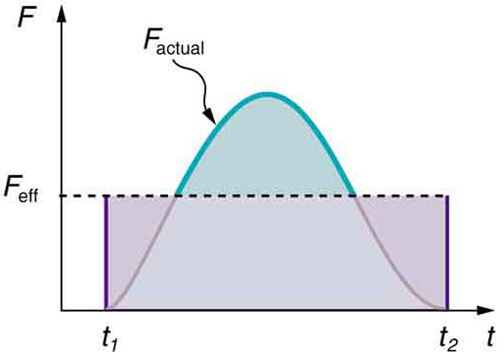
    зображення

    Сила проти часу: Графік сили проти часу з часом вздовж осі x та сили вздовж осі y для фактичної сили та еквівалентної ефективної сили. Області під двома кривими рівні.

    \[\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\]

    Ключові моменти

    • Як і швидкість, лінійний імпульс - це векторна величина, що володіє напрямком, а також величиною.
    • Імпульс, як і енергія, важливий, оскільки це збережена кількість.
    • Імпульс системи частинок - це сума їх моментів. Якщо дві частинки мають маси m 1 і m 2, а швидкості v 1 і v 2, сумарний імпульс дорівнює\(\mathrm{p=p_1+p_2=m_1v_1+m_2v_2.}\).
    • У замкнутій системі без будь-яких зовнішніх сил сумарний імпульс постійний.
    • Знайоме рівняння\(\mathrm{F=ma}\) - це окремий випадок більш загальної форми 2-го закону, коли маса системи постійна.
    • Збереження імпульсу тримається (при відсутності зовнішньої сили) незалежно від характеру міжчастинкової (або внутрішньої) сили, якою б складною не була сила між частинками.
    • Мала сила, прикладена протягом тривалого часу, може спричинити таку ж зміну імпульсу, що і велика сила, прикладена коротко, оскільки важливо саме твір сили та часу, протягом якого вона застосовується.
    • Сила виробляє прискорення, і чим більша сила, що діє на об'єкт, тим більша його зміна швидкості і, отже, більша її зміна імпульсу. Однак зміна імпульсу також пов'язана з тим, як довго діє сила.
    • У разі сили, що змінюється в часі, імпульс може бути розрахований шляхом інтеграції сили протягом тривалості часу. \(\mathrm{Impulse=\int_{t_1}^{t_2} F(t)dt.}\).

    Ключові умови

    • нееластичний: (Що стосується нееластичного зіткнення, на відміну від пружного зіткнення.) Зіткнення, при якому кінетична енергія не зберігається.
    • пружне зіткнення: зустріч між двома тілами, в якій загальна кінетична енергія двох тіл після зустрічі дорівнює їх загальній кінетичній енергії перед зустріччю. Пружні зіткнення відбуваються тільки в тому випадку, якщо немає чистого перетворення кінетичної енергії в інші форми.
    • збереження: Особлива вимірювана властивість ізольованої фізичної системи не змінюється в міру розвитку системи.
    • замкнута система: Фізична система, яка не обмінюється будь-якою матерією зі своїм оточенням і не піддається жодній силі, джерело якої є зовнішнім для системи.
    • імпульс: (тіла в русі) добуток його маси і швидкості.
    • імпульс: Інтеграл сили з плином часу.

    ЛІЦЕНЗІЇ ТА АВТОРСТВА

    CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

    CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ