19.5: Змінні струми

цілі навчання

• Обговорити застосування фазового вектора

Фазори

Складні числа відіграють важливу роль у фізиці. Зазвичай комплексні числа записуються через їх дійсну частину плюс уявна частина. Наприклад,$\mathrm{a+bi}$ де a і b - дійсні числа, а ii сигналізує про уявну частину. Однак часто практичним є написання комплексних чисел у вигляді експоненціальної, званої фазором.

У фізиці фазовий вектор, або фазор, є поданням синусоїдальної функції, амплітуда якої (A), частота (ω) та фаза (θ) є інваріантними в часі, як показано в діаграмі. Фазори розділяють залежності від$A$$ω$, і на$θ$ три незалежні фактори. Це може бути особливо корисно, оскільки частотний фактор (який включає залежність від часу синусоїди) часто є загальним для всіх компонентів лінійної комбінації синусоїдів. У цих ситуаціях фазори дозволяють враховувати цю загальну особливість, залишаючи лише функції A та θ. Результатом є те, що тригонометрія зводиться до алгебри, а лінійні диференціальні рівняння стають алгебраїчними. Тому термін фазор часто стосується лише цих двох факторів.

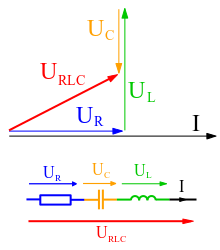
Фазорна діаграма: Приклад послідовної схеми RLC та відповідної фазорної діаграми для конкретного ω. Інженери-електрики, інженери електроніки, техніки електронної техніки та авіаінженери використовують фазорні діаграми для візуалізації складних констант і змінних (фазорів). Як і вектори, стрілки, намальовані на графічному папері або комп'ютерних дисплеях, представляють фазори.

Фазори часто використовуються в електричних системах при розгляді напруг і струмів, які змінюються синусоїдально в часі, наприклад, в ланцюгах RLC.

Визначення

Синусоїди можуть бути представлені математично у вигляді суми двох комплекснозначних функцій:

$$\mathrm { A } \cdot \cos ( \omega t + \theta ) = \mathrm { A } \cdot \dfrac { \mathrm { e } ^ { \mathrm { i } ( \omega t + \theta ) } + \mathrm { e } ^ { - \mathrm { i } ( \omega t + \theta ) } } { 2 }$$

або як реальна частина однієї з функцій:

$$\mathrm { A } \cdot \cos ( \omega t + \theta ) = \operatorname { Re } \left\{ \mathrm { A } \cdot \mathrm { e } ^ { \mathrm { i } ( \omega t + \theta ) } \right\} = \operatorname { Re } \left\{ \mathrm { A } \mathrm { e } ^ { \mathrm { i } \theta } \cdot \mathrm { e } ^ { \mathrm { i } \omega t } \right\}$$

Як зазначалося вище, фазор може посилатися або на AEIEIωtaeIθ EIωT, або просто до комплексної константи, AEIaeiθ. В останньому випадку під ним розуміють стенографічне позначення, що кодує амплітуду і фазу лежить в основі синусоїди.

Фазорне представлення сигналів

Існує дві ключові ідеї, що стоять за фазорним представленням сигналу:

1. реальний сигнал, що змінюється в часі, може бути представлений складним сигналом, що змінюється в часі; і
2. складний сигнал, що змінюється в часі, може бути представлений у вигляді добутку комплексного числа, незалежного від часу і складного сигналу, який залежить від часу.

Сигнал:

$$\mathrm { x } ( \mathrm { t } ) = \operatorname { Acos } ( \omega \mathrm{t} + \theta )$$

показано на малюнку нижче косинусоїдальний сигнал з амплітудою A, частотою та фазою θ. Амплітуда А характеризує коливання піку до піку 2А, кутова частота ω характеризує період T = 2π/ω між негативними до позитивних нульових перетинів (або позитивними піками або негативними піками), а фаза θ характеризує час τ = − θ /ω, коли сигнал досягає свого першого піку. З таким визначенням, сигнал x (t) також може бути записаний як

$$\mathrm { x } ( \mathrm { t } ) = \operatorname { Acos } ( \mathrm { t } - \tau )$$

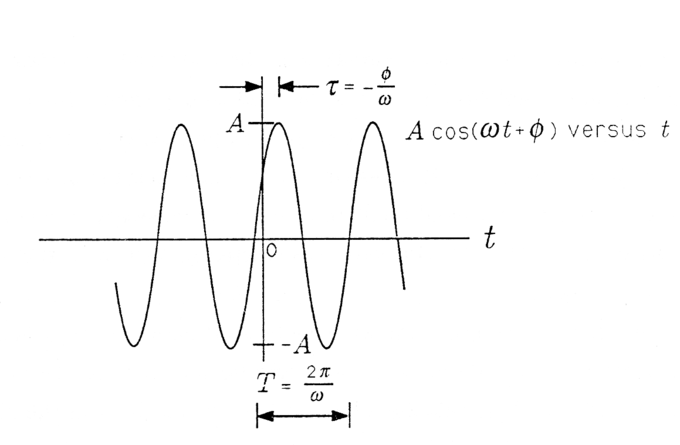
Косинусоїдальний сигнал: косинусоїдальний сигнал.

Коли τ позитивний, то τ - це «затримка часу», яка описує час (більше нуля) при досягненні першого піку. Коли τ негативний, то τ - це «просування часу», яке описує час (менше нуля), коли був досягнутий останній пік. При підстановці =2π/T отримаємо третій спосіб запису x (t):

$$\mathrm { x } ( \mathrm { t } ) = \operatorname { Acos } \frac { 2 \pi } { \mathrm { T } } ( \mathrm { t } - \boldsymbol { \tau } )$$

У такому вигляді сигнал легко піддається сюжету. Просто намалюйте косинусоїдальну хвилю з амплітудою A та періодом T; потім вдарити початок (t = 0), щоб сигнал досяг свого піку при τ. Підводячи підсумок, параметри, що визначають косинусоїдальний сигнал, мають наступні одиниці:

• A, довільний (наприклад, вольт або метрів/сек, залежно від програми)
• ω, в радіанах/сек (рад/сек)
• T, в секундах (сек)
• θ, в радіанах (рад)
• τ, в секундах (сек)

Синусоїдальний стаціонарний стан та серія RLC circuitPhasors можуть бути використані для аналізу поведінки електричних та механічних систем, які досягли свого роду рівноваги, званої синусоїдальним стійким станом.

У синусоїдальному сталому стані кожна напруга і струм (або сила і швидкість) в системі є синусоїдальною з кутовою частотою ω. Однак амплітуди і фази цих синусоїдальних напруг і струмів у всіх різні.

Наприклад, напруга на резисторі може привести напругу на конденсаторі на ⁹⁰ і затримати напругу на індукторі на ⁹⁰. Для того, щоб зробити наше застосування фазорів до електричних систем бетоном, ми розглянемо схему серії RLC, проілюстровану в. Стрілка з позначкою i (t) позначає струм, який протікає у відповідь на прикладену напругу.

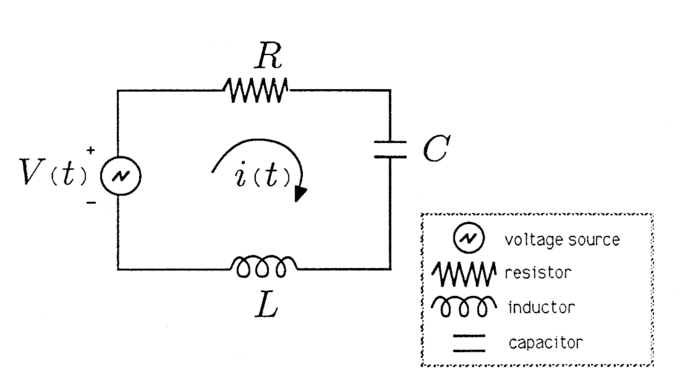
Серія RLC ланцюга: Серія RLC ланцюга.

Будемо вважати, що джерелом напруги є аудіогенератор, який виробляє напругу:

$$\mathrm { V } ( \mathrm { t } ) = \operatorname { Acos } ( \omega \mathrm { t } + \theta )$$

Представляємо цю напругу як складний сигнал:

$$\mathrm { V } ( \mathrm { t } ) \leftrightarrow \mathrm { A } \mathrm { e } ^ { \mathrm { i } \theta } \cdot \mathrm { e } ^ { \mathrm { i } \omega \mathrm { t } }$$

і дати йому фазорове представлення,

$$\mathrm { V } ( \mathrm { t } ) \leftrightarrow \mathrm { V } ; \mathrm { V } = \mathrm { A } \mathrm { e } ^ { \mathrm { i } \theta }$$

Потім ми опишемо джерело напруги фазором V і пам'ятаємо, що ми завжди можемо обчислити фактичну напругу, помноживши на e ^iωt і взявши реальну частину.

Середні квадратні значення

Середньоквадратична (середньоквадратична) напруга або струм - це усереднена за часом напруга або струм в системі змінного струму.

цілі навчання

• Пов'язати середню квадратну напругу і струм в змінному ланцюзі з піковою напругою і струмом і середньою потужністю

Середні квадратні значення та змінний струм

Нагадаємо, що в разі змінного струму (змінного струму) потік електричного заряду періодично змінює напрямок. На відміну від постійного струму (DC), де струми і напруги постійні, змінні струми і напруги змінюються з часом. Нагадаємо, що більшість житлових і комерційних джерел живлення використовують змінний струм. Часто буває так, що ми хочемо знати час усередненого струму, або напруги. Враховуючи струм або напругу як функцію часу, ми можемо взяти середній квадрат кореня з часом, щоб повідомити середні величини.

Визначення

Середній квадрат кореня (скорочено середньоквадратичний або середньоквадратичний), також відомий як середнє квадратичне, є статистичною мірою величини різної величини. Це особливо корисно, коли функція чергується між додатними і від'ємними значеннями, наприклад, синусоїдами.Середньоквадратичне значення набору значень (або функція безперервного часу, така як синусоїда) є квадратним коренем середнього арифметичного квадратів вихідних значень (або квадрата функції). У випадку множини n значень {x ₁, x ₂,... , x _n}, середньоквадратичне значення задається за такою формулою:

$$\mathrm { x } _ { \mathrm { rms } } = \sqrt { \dfrac { 1 } { \mathrm { n } } \left( \mathrm { x } _ { 1 } ^ { 2 } + \mathrm { x } _ { 2 } ^ { 2 } + \cdots + \mathrm { x } _ { \mathrm { n } } ^ { 2 } \right) }$$

Відповідна формула для неперервної функції f (t), визначеної через інтервал T ₁ ≤ t ≤ T ₂, виглядає наступним чином:

$$\mathrm { f } _ { \mathrm { rms } } = \sqrt { \dfrac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } \int _ { \mathrm { T } _ { 1 } } ^ { \mathrm { T } _ { 2 } } [ \mathrm { t } ( \mathrm { t } ) ] ^ { 2 } \mathrm { d } \mathrm { t } }$$

Середньоквадратичне значення для функції протягом усього часу знаходиться нижче.

$$\mathrm { f } _ { \mathrm { rms } } = \lim _ { T \rightarrow \infty } \sqrt { \dfrac { 1 } { \mathrm { T } } \int _ { 0 } ^ { \mathrm { T } } [ \mathrm { t } ( \mathrm { t } ) ] ^ { 2 } \mathrm { d } t }$$

Середньоквадратичне значення за весь час періодичної функції дорівнює середньоквадратичному значенню одного періоду функції. Середньоквадратичне значення безперервної функції або сигналу можна наблизити, взявши середньоквадратичне значення серії однаково розташованих зразків.

Застосування до напруги та струму

Розглянемо випадок синусоїдально змінної напруги:

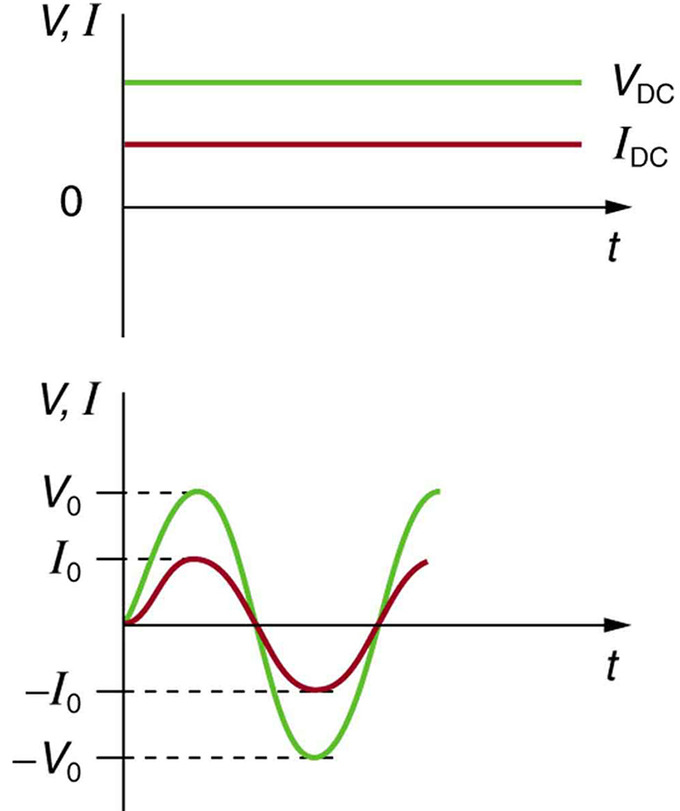
Синусоїдальна напруга і струм: (а) Напруга постійного струму і струм є постійними в часі, після встановлення струму. (b) Графік напруги та струму в порівнянні з часом для 60 Гц змінного струму. Напруга і струм синусоїдальні і знаходяться в фазі для простого ланцюга опору. Частоти і пікові напруги джерел змінного струму сильно відрізняються.

$$\mathrm { V } = \mathrm { V } _ { 0 } \sin ( 2 \pi \mathrm { ft } )$$

V - напруга в момент t, V ₀ - пікова напруга, а f - частота в герцах. Для цієї простої ланцюга опору I = V/R, і тому струм змінного струму виглядає наступним чином:

$$\mathbf { I } = \mathbf { I } _ { 0 } \sin ( 2 \pi \mathrm { ft } )$$

Тут I - струм в момент t, а I ₀ = V ₀ /R - піковий струм. Тепер скориставшись визначенням вище, розрахуємо середньоквадратичне напруга і середньоквадратичний струм. По-перше, у нас є

$$\mathrm { V } _ { \mathrm { rms } } = \sqrt { \dfrac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } } \int _ { \mathrm { T } _ { 1 } } ^ { \mathrm { T } _ { 2 } } \left[ \mathrm { V } _ { 0 } \sin ( \omega \mathrm { t } ) \right] ^ { 2 } \mathrm { d } \mathrm { t }$$

Тут ми замінили 2πf на ω. Оскільки V ₀ є константою, ми можемо перерахувати його з квадратного кореня та використовувати ідентифікатор трига для заміни функції квадрата синуса.

$$\mathrm { V } _ { \mathrm { rms } } = \mathrm { V } _ { 0 } \sqrt { \dfrac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } } \int _ { \mathrm { T } _ { 1 } } ^ { \mathrm { T } _ { 2 } } \dfrac { 1 - \cos ( 2 \omega t ) } { 2 } \mathrm { d } t$$

Інтегруючи вищевикладене, ми маємо:

$$\mathrm { V } _ { \mathrm { rms } } = \mathrm { V } _ { 0 } \sqrt { \dfrac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } \left[ \dfrac { t } { 2 } - \dfrac { \sin ( 2 \omega t ) } { 4 \omega } \right] _ { \mathrm { T } _ { 1 } } ^ { \mathrm { T } _ { 2 } } }$$

Оскільки інтервал являє собою цілу кількість повних циклів (за визначенням RMS), терміни скасують, залишивши:

$$\mathrm { V } _ { \mathrm { rm } } = \mathrm { V } _ { 0 } \sqrt { \frac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } \left[ \dfrac { \mathrm { t } } { 2 } \right] \mathrm { T } _ { 1 } } = \mathrm { V } _ { 0 } \sqrt { \dfrac { 1 } { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } \dfrac { \mathrm { T } _ { 2 } - \mathrm { T } _ { 1 } } { 2 } }$$

$$= \dfrac { V _ { 0 } } { \sqrt { 2 } }$$

Аналогічним чином можна виявити, що середньоквадратичний струм може бути виражений досить просто:

$$\mathrm { I } _ { \mathrm { rms } } = \mathrm { I } _ { 0 } / \sqrt { 2 }$$

Оновлені рівняння ланцюга для змінного струму

Багато рівнянь, які ми вивели для постійного струму, однаково застосовуються до змінного струму. Якщо ми стурбовані часом усереднений результат і відповідні змінні виражаються у вигляді їх середньоквадратичних значень. Наприклад, Закон Ома для АС пишеться так:

$$\mathrm { I } _ { \mathrm { rms } } = \dfrac { \mathrm { V } _ { \mathrm { rms } } } { \mathrm { R } }$$

Різні вирази для живлення змінного струму наведені нижче:

$$\mathrm { P } _ { \mathrm { ave } } = \mathrm { I } _ { \mathrm { rms } } \mathrm { V } _ { \mathrm { rms } }$$

$$\mathrm { P } _ { \mathrm { ave } } = \dfrac { \mathrm { V } _ { \mathrm { ms } } ^ { 2 } } { \mathrm { R } }$$

$$\mathrm { P } _ { \mathrm { ave } } = \mathrm { I } _ { \mathrm { rms } } ^ { 2 } \mathrm { R }$$

З наведених вище рівнянь видно, що ми можемо висловити середню потужність як функцію пікової напруги та струму (у випадку синусоїдально змінного струму та напруги):

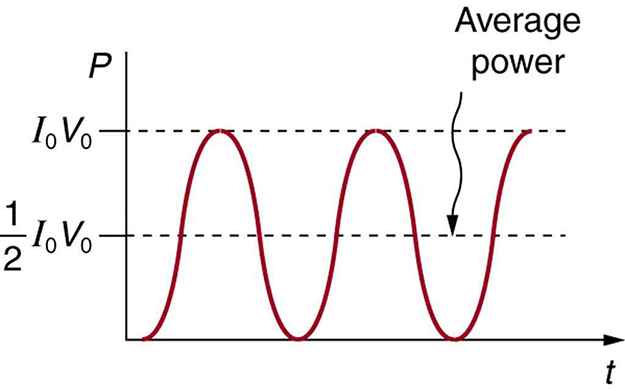
Середня потужність: потужність змінного струму як функція часу. Оскільки напруга і струм знаходяться тут у фазі, їх твір ненегативний і коливається між нулем і I0V0. Середня потужність становить (1/2) I0V0.

$$\mathrm { P } _ { \mathrm { ave } } = \mathrm { I } _ { \mathrm { rms } } V _ { \mathrm { rms } } = \dfrac { \mathrm { I } _ { 0 } } { \sqrt { 2 } } \dfrac { \mathrm { V } _ { 0 } } { \sqrt { 2 } } = \dfrac { 1 } { 2 } \mathrm { V } _ { 0 } \mathrm { I } _ { 0 }$$

Значення RMS також корисні, якщо напруга змінюється на деяку форму хвилі, відмінну від синусоїдів, наприклад, з квадратними, трикутними або пилкоподібними хвилями.

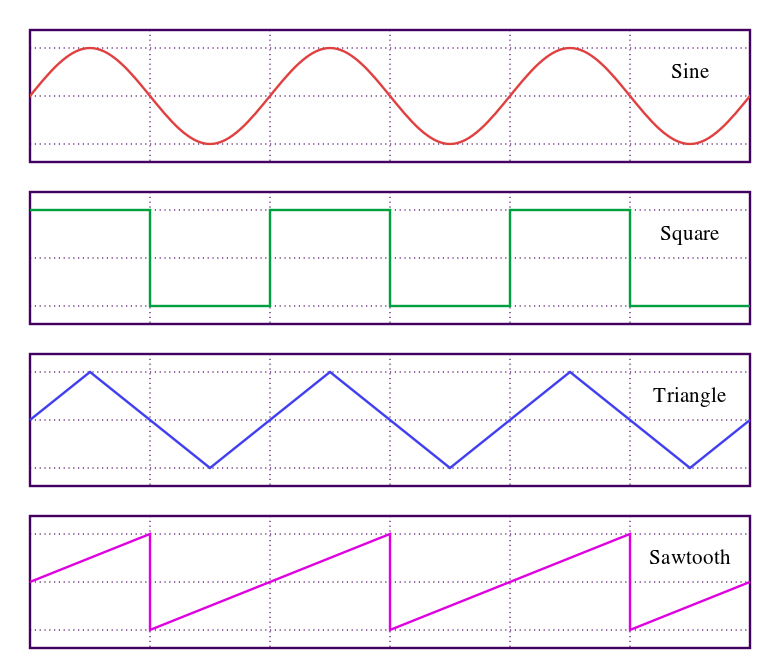
Форми хвиль: синусоїда, квадрат, трикутник та пилкоподібні форми хвиль

Техніка безпеки в домашньому господарстві

Системи та пристрої електробезпеки розроблені та широко використовуються для зменшення ризиків термічної та ударної небезпеки.

цілі навчання

• Визначте основні ризики, пов'язані з електричними ланцюгами та стратегії зменшення цих ризиків

Електробезпека та побутова техніка

Електрика має дві небезпеки. Теплова небезпека виникає у випадках електричного перегріву. Небезпека удару виникає при проходженні електричного струму через людину. Існує безліч систем і пристроїв, що запобігають електричну небезпеку.

Безпека змінного струму: Схема простого ланцюга змінного струму з джерелом напруги та одним приладом, представленим опором R.

На практиці проста схема змінного струму без функцій безпеки - це не те, як розподіляється потужність. Сучасна побутова і промислова електропроводка вимагає трижильної системи, що володіє декількома особливостями безпеки. Першою особливістю безпеки є звичний автоматичний вимикач (або запобіжник), який запобігає теплове перевантаження. По-друге, навколо приладу є захисний чохол, як у тостера або холодильника. Корпус заважає людям торкатися відкритих проводів і вступати в електричний контакт з ланцюгом, допомагаючи запобігти ударам.

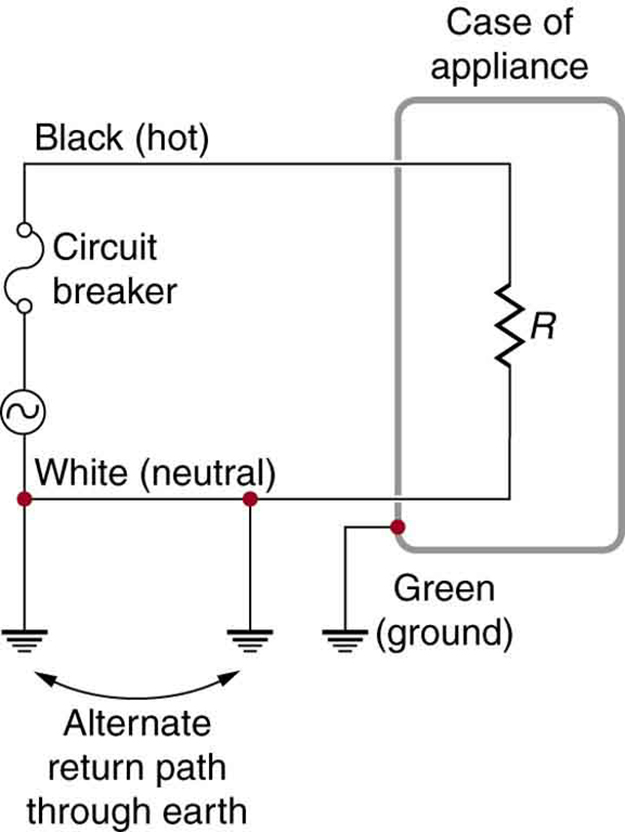
Трипровідна система: Трипровідна система з'єднує нейтральний провід із землею в джерелі напруги та місці користувача. Він існує при нульових вольтах і подає альтернативний зворотний шлях для струму через землю. Корпус приладу також заземлений на нуль вольт. Автоматичний вимикач або запобіжник запобігає тепловому перевантаженню і існує послідовно на активному (живі/гарячому) дроті. Кольори ізоляції проводів варіюються в залежності від регіону. Важливо перевірити локально, щоб визначити, які колірні коди використовуються, навіть якщо вони були дотримані в одній конкретній установці.

Є три з'єднання з землею або землею (земля/земля,). З'єднання заземлення/заземлення - це шлях низького опору безпосередньо до землі. Два з'єднання заземлення/заземлення на нульовому проводі змушують його існувати при нульових вольтах щодо землі, даючи проводу свою назву. Таким чином, цей провід безпечний для дотику, навіть якщо його ізоляція відсутня. Нейтральний провід - це зворотний шлях для струму, щоб слідувати, щоб завершити ланцюг.

Два заземлення/заземлення забезпечують альтернативний шлях через землю для завершення ланцюга, оскільки земля є хорошим провідником. Підключення заземлення/заземлення, найближче до джерела живлення, може знаходитися на генеруючій установці, тоді як інше - за місцем розташування користувача. Третє підключення заземлення/заземлення передбачає корпус приладу, через зелений провід заземлення/заземлення, змушуючи корпус знаходитися на нульових вольтах. Живий або гарячий провід (живий/гарячий) подає напругу і струм для роботи приладу. Трьохпровідна система підключається до електроприладу через трьохконтактний штекер.

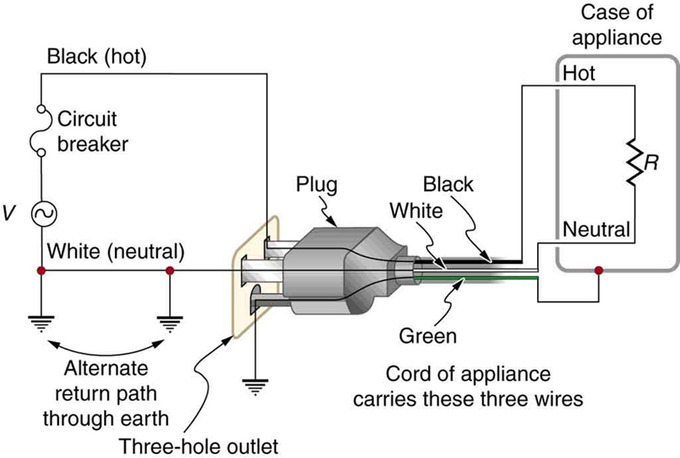
Трьохконтактний штекер: Стандартний штекер із трьома зубцями можна вставити лише одним способом, щоб забезпечити належну функцію трипровідної системи.

Трьохконтактний штекер

Трижильна система замінила стару двожильну систему, в якій відсутній провід заземлення/заземлення. За звичайних обставин ізоляція на живих/гарячих та нейтральних проводах запобігає розміщенню корпусу безпосередньо в ланцюзі, так що провід заземлення/заземлення може здатися подвійним захистом. Однак заземлення корпусу вирішує не одну проблему. Найпростіша проблема - зношена ізоляція на живий/гарячий провід, що дозволяє йому контактувати з корпусом. При відсутності заземлення/заземлення (деякі люди відрізають третій зубець від вилки, оскільки у них є лише застарілі розетки з двома отворами), можливий сильний шок. Особливо небезпечно це на кухні, де є гарне підключення заземлення/заземлення через воду на підлозі або водопровідний кран.

При неушкодженому підключенні заземлення/заземлення автоматичний вимикач спрацьовує, тим самим вимагаючи ремонту приладу. Деякі прилади все ще продаються з двоконтактними вилками. Ці прилади, в тому числі електроінструменти з ударостійкими пластиковими корпусами, мають непровідні корпуси і називаються «подвійно ізольованими». сучасні двоконтактні вилки можуть бути вставлені в асиметричну стандартну розетку тільки одним способом, забезпечуючи належне з'єднання живих/гарячих і нейтральних проводів.

Кольорове кодування

Ізоляційний пластик має кольорове маркування для ідентифікації живих/гарячих, нейтральних та заземлюючих проводів, але ці коди різняться у всьому світі. Живі/гарячі дроти можуть бути коричневими, червоними, чорними, синіми або сірими. Нейтральні дроти можуть бути синього, чорного або білого кольору. Оскільки один і той же колір може використовуватися для живих/гарячих або нейтральних проводів у різних куточках світу, важливо підтвердити колірний код для будь-якого конкретного локального регіону. Єдиним винятком є заземлення/заземлення, який часто зелений, але може бути жовтим або «оголеним проводом». смугасті покриття іноді використовуються на користь тих, хто дальтонік.

Струм індукції та витоку

Електромагнітна індукція викликає більш тонку проблему, вирішену заземленням корпусу. Змінний струм в приладах може викликати ЕРС на корпусі. Якщо заземлено, напруга корпусу тримається біля нуля, але якщо корпус не заземлений, може статися удар. Струм, який приводиться в дію ЕРС індукованого корпусу, називається струмом витоку, хоча струм не обов'язково проходить від резистора до корпусу.

Ключові моменти

• Фазор - це подання синусоїдальної функції, амплітуда (A), частота (ω) та фаза (θ) є інваріантними у часі. Якщо ω ділиться всіма компонентами системи, це може бути враховано, залишивши лише A і ω. Термін фазор зазвичай відноситься до двох останніх факторів.
• Фазори значно знижують складність вираження синусоїдально змінюються сигналів.
• Фазори можуть бути використані для аналізу поведінки електричних систем, таких як схеми RLC, які досягли своєрідної рівноваги, званої синусоїдальним стаціонарним станом. У синусоїдальному сталому стані кожна напруга і струм в системі є синусоїдальною з кутовою частотою ω.
• Фазори дозволяють нам застосовувати методи, що використовуються для вирішення ланцюгів постійного струму для вирішення RC-ланцюгів.
• Нагадаємо, що на відміну від постійного струму і напруги, які є постійними, змінний струм і напруга змінюються з часом. Це називається змінним струмом, оскільки напрямок чергується.
• Середній квадрат кореня (скорочено середньоквадратичне або середньоквадратичне значення) - це статистична міра величини різної величини. Ми використовуємо середній квадрат кореня для вираження середнього струму або напруги в системі змінного струму.
• Середньоквадратичним струмом і напругою (для синусоїдальних систем) є піковий струм і напруга над квадратним коренем двох.
• Середня потужність в ланцюзі змінного струму - це твір середньоквадратичного струму і середньоквадратичного напруги.
• Електричні ланцюги несуть ризики перегріву та потенційних ударів електричним струмом.
• Запобіжники і автоматичні вимикачі використовуються для зупинки струмів, що перевищують встановлену межу безпеки, запобігаючи тим самим перегрів.
• Трипровідна система захищає від термічних та ударних небезпек, використовуючи живі, нейтральні та заземлюючі дроти, а також заземлення нульового проводу та провідних корпусів приладів.
• Перш ніж переробляти будь-яку схему, важливо встановити правильну схему колірного кодування для вашого регіону (колір живих/гарячих, нейтральних і заземлюючих проводів).
• Змінний струм має потенціал викликати ЕРС на корпусі приладу, що становить небезпеку удару, тому важливо заземлити корпус.

Ключові умови

• синусоїдальний сталий стан: Вказує, що кожна напруга і струм в системі є синусоїдальним з однаковою кутовою частотою ω.
• комплексні числа: числа, які мають уявну частину. Зазвичай представлений у вигляді i.
• фазор: представлення комплексного числа в терміні комплексної експоненції.
• Середній квадрат: Квадратний корінь середнього арифметичного квадратів.
• середньоквадратичний струм: середній квадрат струму$\mathrm{I_{rms}=\frac{I_0}{\sqrt{2}}}$, де I0 - піковий струм, в системі змінного струму
• середньоквадратична напруга: середній квадрат напруги$\mathrm{V_{rms}=\frac{V_0}{\sqrt{2}}}$, де V0 - пікова напруга, в системі змінного струму
• термічна небезпека: електрична небезпека, спричинена перегрівом (наприклад, в резистивному елементі)
• шокова небезпека: електрична небезпека, яка становить ризик проходження струму через тіло
• трипровідна система: сучасна система електропроводки з технікою безпеки; містить живий, нейтральний і заземлюючий дроти

ЛІЦЕНЗІЇ ТА АВТОРСТВА

CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

• Курація та доопрацювання. Надано: Boundless.com. Ліцензія: CC BY-SA: Із Зазначенням Авторства

CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ

• Білл Вілсон, Огляд фазорів. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m11381/latest/. Ліцензія: CC BY: Зазначення авторства
• Луї Шарф, Фазори: Фазорне представлення сигналів. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21474/latest/. Ліцензія: CC BY: Зазначення авторства
• Луї Шарф, Фазори: синусоїдальний стійкий стан та ланцюг серії RLC. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21475/latest/. Ліцензія: CC BY: Зазначення авторства
• Фазора. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Фазор. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• фазора. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/phasor. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• синусоїдальний стійкий стан. Надано: Вікіпедія. Розташований за адресою: en.wikipedia.org/wiki/Синусоїдаль% 20 Стан. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• комплексні числа. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/complex_numbers. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Луї Шарф, Фазори: Фазорне представлення сигналів. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21474/latest/. Ліцензія: CC BY: Зазначення авторства
• Фазора. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Фазор. Ліцензія: Суспільне надбання: Немає відомих авторських прав
• Луї Шарф, Фазори: синусоїдальний стійкий стан та ланцюг серії RLC. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21475/latest/. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 18 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42348/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Корінь середній квадрат. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Корень_меан_сквер. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Безмежний. Надано: Безмежне навчання. Розташований за адресою: www.boundless.com//фізика/визначення/RMS-напруга. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Безмежний. Надано: Безмежне навчання. Розташований за адресою: www.boundless.com//фізика/визначення/RMS-поточний. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• корінь середній квадрат. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/root_mean_square. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Луї Шарф, Фазори: Фазорне представлення сигналів. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21474/latest/. Ліцензія: CC BY: Зазначення авторства
• Фазора. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Фазор. Ліцензія: Суспільне надбання: Немає відомих авторських прав
• Луї Шарф, Фазори: синусоїдальний стійкий стан та ланцюг серії RLC. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21475/latest/. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 29 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42348/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Корінь середній квадрат. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Корень_меан_сквер. Ліцензія: Суспільне надбання: Немає відомих авторських прав
• Коледж OpenStax, Коледж фізики. 29 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42348/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Безмежний. Надано: Безмежне навчання. Розташований за адресою: www.boundless.com//фізика/визначення/термічна небезпека. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Коледж OpenStax, Коледж фізики. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42416/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Безмежний. Надано: Безмежне навчання. Розташований за адресою: www.boundless.com//physics/визначення/трипровідна система. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Безмежний. Надано: Безмежне навчання. Розташований за адресою: www.boundless.com//фізика/визначення/шок-небезпека. Ліцензія: CC BY-SA: Із Зазначенням Авторства
• Луї Шарф, Фазори: Фазорне представлення сигналів. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21474/latest/. Ліцензія: CC BY: Зазначення авторства
• Фазора. Надано: Вікіпедія. Знаходиться за адресою: http://en.Wikipedia.org/wiki/Phasor. Ліцензія: Суспільне надбання: Немає відомих авторських прав
• Луї Шарф, Фазори: синусоїдальний стійкий стан та ланцюг серії RLC. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m21475/latest/. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 29 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42348/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Корінь середній квадрат. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Корень_меан_сквер. Ліцензія: Суспільне надбання: Немає відомих авторських прав
• Коледж OpenStax, Коледж фізики. 29 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42348/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 30 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42416/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 30 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42416/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства
• Коледж OpenStax, Коледж фізики. 30 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42416/latest/?collection=col11406/1.7. Ліцензія: CC BY: Зазначення авторства