17.3: Закон Кулона

Last updated

Oct 27, 2022
Save as PDF
- 17.2: Укриття та зарядка через індукцію
- 17.4: Повторний перегляд електричного поля

Boundless
Boundless

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

навчальні цілі

Застосуйте принцип суперпозиції для визначення чистої реакції, викликаної двома або більше подразниками

Принцип суперпозиції (також відомий як властивість суперпозиції) стверджує, що: для всіх лінійних систем чиста реакція в даному місці та часі, викликана двома або більше стимулами, - це сума відповідей, які були б викликані кожним стимулом окремо. Для закону Кулона подразники - це сили. Тому принцип говорить про те, що сумарна сила - це векторна сума окремих сил.

Кулонівський Сили

Скалярна форма Закону Кулона пов'язує величину і знак електростатичної сили F, що діє одночасно на два точкових заряди q ₁ і q ₂:

$| \mathrm { F } | = \dfrac { 1 } { 4 \pi a r \epsilon _ { 0 } } \dfrac { \left| q _ { 1 } q _ { 2 } \right| } { \mathrm { r } ^ { 2 } }$

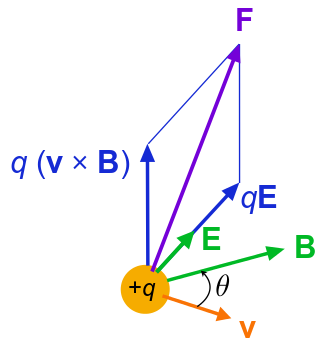
зображення

Сила Лоренца на рухому частинку: сила Лоренца f на заряджену частинку (заряду q) в русі (миттєва швидкість v). Поле E та B змінюються за простором і часом.

де r - відстань поділу, а ε ₀ - електрична діелектрична проникність. Якщо твір q ₁ q ₂ позитивне, сила між ними відштовхує; якщо q ₁ q ₂ негативна, сила між ними приваблива. Принцип лінійної суперпозиції дозволяє розширенню закону Кулона включати будь-яку кількість точкових зарядів - для того, щоб вивести силу на будь-якому одному точковому заряді шляхом векторного додавання цих окремих сил, що діють окремо на цьому точковому заряді. Отриманий вектор сили виявляється паралельним вектору електричного поля в цій точці, з видаленням цього точкового заряду.

Для обчислення сили на малому випробувальному заряді q в позиції rr, за рахунок системи N дискретних зарядів:

$\mathrm{F(r)=\dfrac{q}{4πarϵ_0} }\sum _ { i = 1 } ^ { N } q _ { i } \frac { \mathrm { r } - \mathrm { r } _ { \mathrm { i } } } { \left| \mathrm { r } - \mathrm { r } _ { \mathrm { i } } \right| ^ { 3 } } = \frac { q } { r 4 \pi a r \epsilon _ { 0 } }\sum _ { \mathrm { i } = 1 } ^ { \mathrm { N } } \mathrm { q } _ { \mathrm { i } } \dfrac { \hat { \mathrm { R } _ { i } } } { \left| \mathrm { R } _ { \mathrm { i } } \right| ^ { 2 } }$

де q _i і r _i - вектор величини і положення i-го заряду відповідно і $\hat { \mathrm { R } _ { \mathrm { i } } }$ є одиничним вектором у напрямку $\mathrm { R } _ { \mathrm { i } } = \mathrm { r } - \mathrm { r } _ { \mathrm { i } }$ (вектор, що вказує від зарядів q _i до q.)

Звичайно, наше обговорення суперпозиції сил стосується будь-яких типів (або комбінацій) сил. Наприклад, коли заряд рухається в присутності магнітного поля, а також електричного поля, заряд буде відчувати як електростатичні, так і магнітні сили. Сумарна сила, що впливає на рух заряду, буде векторною сумою двох сил. (У цьому конкретному прикладі рухомого заряду сила, обумовлена наявністю електромагнітного поля, в сукупності називається силою Лоренца (див.).

Сферичний розподіл заряду

Розподіл заряду навколо молекули має сферичну природу і створює своєрідну електростатичну «хмару» навколо молекули.

навчальні цілі

Опишіть форму кулонівської сили від сферичного розподілу заряду

Завдяки роботі вчених наприкінці 18 століття основні риси електростатичної сили - існування двох типів заряду, спостереження, які подібно до зарядів відштовхуються, на відміну від зарядів притягуються, і зменшення сили з відстанню - були врешті-решт уточнені і виражені у вигляді математичної формули. Математична формула електростатичної сили називається законом Кулона після французького фізика Шарля Кулона (1736—1806), який проводив експерименти і вперше запропонував формулу для її обчислення.

зображення

Розподіл заряду в молекулі води: Схематичне зображення зовнішньої електронної хмари нейтральної молекули води. Електрони проводять більше часу поблизу кисню, ніж водні, даючи постійне поділ заряду, як показано. Вода, таким чином, є полярною молекулою. На нього легше впливають електростатичні сили, ніж молекули з рівномірним розподілом заряду.

Сучасні експерименти перевірили закон Кулона з великою точністю. Наприклад, було показано, що сила обернено пропорційна відстані між двома об'єктами в квадраті (F1/r ²) з точністю 1 частина в 1016. Ніяких винятків ніколи не було знайдено, навіть на малих відстанях всередині атома.

Закон Кулона тримається навіть всередині атомів, правильно описуючи силу між позитивно зарядженим ядром і кожним з негативно заряджених електронів. Цей простий закон також правильно враховує сили, які зв'язують атоми разом, утворюючи молекули, і сили, які зв'язують атоми та молекули разом, утворюючи тверді тіла та рідини.

Як правило, зі збільшенням відстані між іонами енергія тяжіння наближається до нуля, а іонне з'єднання менш сприятливе. Зі збільшенням величини протилежних зарядів енергія збільшується і іонне зв'язування є більш сприятливим.

Електричне поле - це векторне поле, яке пов'язує з кожною точкою простору кулонівську силу, яка буде відчувати тестовий заряд єдності. З огляду на електричне поле напруженість і напрямок сили F на величину заряду q в електричному полі E визначається електричним полем. Для позитивного заряду напрямок електричного поля вказує по лініях, спрямованих радіально в сторону від місця точкового заряду, тоді як напрямок - в бік для негативного заряду.

Цей розподіл навколо зарядженої молекули має сферичну природу і створює своєрідну електростатичну «хмару» навколо молекули. Сили тяжіння або відштовхування в межах сферичного розподілу заряду сильніше ближче до молекули, і стають слабшими у міру збільшення відстані від молекули.

Це зображення показує зовнішню електронну хмару нейтральної молекули води. Розподіл заряду молекули кисню негативний і притягує дві позитивні молекули водню. Тяжіння між двома протилежними зарядами утворює нейтральну молекулу води. Це полярна молекула, оскільки все ще існує постійне поділ заряду, оскільки електрони проводять більше часу поблизу кисню, ніж водні.

Розв'язування задач з векторами та законом Кулона

Закон Кулона, який обчислює електричну силу між зарядженими частинками, можна записати в векторні позначення як $\mathrm { F } ( \mathrm { E } ) = \frac { \mathrm { kq } _ { 1 } \mathrm { q } _ { 2 } } { \mathrm { r } ^ { 2 } } \mathrm { r } +$ .

навчальні цілі

Поясніть, коли можна використовувати векторні позначення Закону Кулона

Розв'язування задач з векторами та законом Кулона

Електрична сила між двома точковими зарядами

Для вирішення електростатичних сил серед електрично заряджених частинок спочатку розглянемо дві частинки з електричними зарядами q і Q, розділені в порожньому просторі на відстань r Припустимо, що ми хочемо знайти вектор електричної сили на заряді q. (вектор електричної сили має як величину, так і напрямок.) Ми можемо висловити розташування заряду q як r _q, а місце заряду Q як r _Q. Таким чином ми можемо знати як сильну електричну силу на заряді, так і в якому напрямку спрямована ця сила. Закон Кулона з використанням векторів можна записати так:

$\mathbf { F } _ { \mathbf { E } } = \dfrac { \operatorname { kq } Q \left( \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right) } { \left| \mathrm { r } _ { \mathrm { q } } - \mathrm { r } _ { Q } \right| ^ { 3 } }$

У цьому рівнянні k дорівнює $\frac { 1 } { 4 \pi \varepsilon _ { 0 } \varepsilon }$ , де $\varepsilon _ { 0 }$ діелектрична проникність вільного простору і εε - відносна діелектрична проникність матеріалу, в який занурені заряди. Змінні $\mathbf { F} _ { \mathbf { E } } , \mathbf { \Gamma } _ { \mathrm { q } }$ і $\mathbf{ R}_Q$ виділені жирним шрифтом, оскільки вони є векторами. Таким чином, нам потрібно знайти, $\mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { Q } }$ виконавши стандартне векторне віднімання. Це означає, що нам потрібно відняти відповідні компоненти вектора $\mathbf{r}_\mathrm{Q}}$ з вектора $\mathrmbf{r}_\mathrm{q}$ .

Це векторне позначення може бути використано в простому прикладі двох точкових зарядів, де тільки один з яких є джерелом заряду.

зображення

Застосування закону Кулона: У простому прикладі векторне позначення Закону Кулона може бути використано, коли є два точкові заряди і лише один з яких є джерельним зарядом.

Електрична сила на польовому заряді за рахунок зарядів фіксованого джерела

Припустимо, що існує більше одного точкового джерела зарядів, що забезпечують сили на поле заряду. діаграми досить простий приклад з трьома джерельними зарядами (показаними зеленим кольором і індексованими індексами) і одним польовим зарядом (червоним кольором, позначено q). Припускаємо, що вихідні заряди фіксуються в просторі, а польовий заряд q підпорядкований силам від вихідних зарядів.

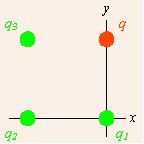
зображення

Кілька точкових зарядів: Закон Кулона застосовується до більш ніж одного точкового джерела зарядів, що забезпечують сили на польовому заряді.

Зверніть увагу на вибрану систему координат. Усі заряди лежать на кутах квадрата, а початок вибирається для співставлення з нижнім правим джерелом заряду та вирівнюється з квадратом. Оскільки ми можемо мати лише одне походження координат, у початку може лежати не більше однієї з вихідних точок, а зміщення від різних вихідних точок до точки поля відрізняються. Сумарна сила на польовий заряд q обумовлена додатками сили, описаної в векторному позначенні Закону Кулона від кожного з вихідних зарядів. Отже, загальна сила є сумою цих індивідуальних сил.

зображення

Зсуви польового заряду: Зсуви польового заряду від кожного заряду джерела показані у вигляді світло-синіх стрілок.

Застосування Закону Кулона тричі та підведення підсумків дає нам:

$\mathbf { F } _ { \mathbf { E } _ { \mathbf { q } } } =\dfrac { \operatorname { kq } \cdot q _ { 1 } \left( \mathbf { r } _ { q } - \mathbf { r } _ { q 1 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 1 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathbf { q } _ { 2 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 2 } \right| ^ { 3 } }+ \dfrac { \mathrm { kq } \cdot \mathrm { q } _ { 3 } \left( \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right) } { \left| \mathbf { r } _ { \mathrm { q } } - \mathbf { r } _ { \mathrm { q } 3 } \right| ^ { 3 } }$

Це рівняння можна додатково спростити і застосувати до фіксованої кількості точок заряду.

$\mathbf { F } _ { \mathbf { n } } =\sum _ { i \neq n }\dfrac { q _ { n } q _ { i } \left( \mathbf { r } _ { n } - \mathbf { r } _ { i } \right) } { 4 \pi \epsilon _ { 0 } \left| \mathbf { r } _ { \mathrm { n } } - \mathbf { r } _ { \mathrm { i } } \right| ^ { 3 } }$

Закон Кулона: У цьому відео я продовжую свою серію навчальних відео з електростатики. Він розбивається на рівні бакалаврату, і хоча він в основному спрямований на фізику спеціальностей, він повинен бути корисним для тих, хто приймає перший курс з електрики та магнетизму, таких як інженери тощо.

Ключові моменти

Принцип суперпозиції передбачає, що чиста реакція в даному місці та часі, викликана двома або більше подразниками, є сумою відповідей, які були б викликані кожним стимулом окремо.
Загальна кулонівське зусилля на випробувальному заряді за рахунок групи зарядів дорівнює векторній сумі всіх кулонівських сил між випробувальним зарядом і іншими окремими зарядами.
Накладення сил не обмежується кулонівськими силами. Він застосовується до будь-яких типів (або комбінацій) сил.
Сила між двома предметами обернено пропорційна квадрату відстані між двома об'єктами.
Сили тяжіння або відштовхування в межах сферичного розподілу заряду сильніше ближче до молекули і стають слабшими у міру збільшення відстані від молекули.
Цей закон також враховує сили, які зв'язують атоми разом, утворюючи молекули, і сили, які зв'язують атоми та молекули разом, утворюючи тверді тіла та рідини.
Векторне позначення Закону Кулона може бути використано в простому прикладі двох точкових зарядів, де тільки один з яких є джерелом заряду.
Сумарна сила на польовому заряді для множинних точкових зарядів джерела є сумою цих індивідуальних сил.
Закон Кулона може бути додатково спрощений і застосований до фіксованої кількості балів заряду.

Ключові елементи

Сила Лоренца: Сила, що чиниться на заряджену частинку в електромагнітному полі.
одиничний вектор: вектор з довжиною 1.
електростатична сила: електростатична взаємодія між електрично зарядженими частинками; кількість і напрямок тяжіння або відштовхування між двома зарядженими тілами.
закон Кулона: математичне рівняння, що обчислює вектор електростатичної сили між двома зарядженими частинками

ЛІЦЕНЗІЇ ТА АВТОРСТВА

CC ЛІЦЕНЗОВАНИЙ КОНТЕНТ, РАНІШЕ ДІЛИВСЯ

Курація та доопрацювання. Надано: Boundless.com. Ліцензія: CC BY-SA: Із Зазначенням Авторства

CC ЛІЦЕНЗОВАНИЙ ВМІСТ, СПЕЦИФІЧНА АТРИБУЦІЯ

Закон Кулона. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Coulomb's_law. Ліцензія: CC BY-SA: Із Зазначенням Авторства
електростатична сила. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Електростатика% 20 сила. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Лоренца сила. Надано: Вікісловник. Розташоване за адресою: uk.wiktionary.org/wiki/Лоренц_форс. Ліцензія: CC BY-SA: Із Зазначенням Авторства
одиниця вектора. Надано: Вікісловник. Розташований за адресою: uk.wiktionary.org/wiki/unit_vector. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Лоренца сила. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Lorentz_force. Ліцензія: CC BY: Зазначення авторства
Відкритий податковий коледж, Закон Coulombu2019. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42308/latest/. Ліцензія: CC BY: Зазначення авторства
Закон Кулона. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Coulomb's_law. Ліцензія: CC BY-SA: Із Зазначенням Авторства
електростатична сила. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Електростатика% 20 сила. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Лоренца сила. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Lorentz_force. Ліцензія: CC BY: Зазначення авторства
Відкритий податковий коледж, Закон Coulombu2019. 25 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42308/latest/. Ліцензія: CC BY: Зазначення авторства
Джордж Браун, Закон Кулона. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m12742/latest/. Ліцензія: CC BY: Зазначення авторства
Джордж Браун, CLF Кілька точкових джерел. 17 вересня 2013 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m12747/latest/. Ліцензія: CC BY: Зазначення авторства
Закон Кулона. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Coulomb's_law. Ліцензія: CC BY-SA: Із Зазначенням Авторства
електростатична сила. Надано: Вікіпедія. Розташований за адресою: uk.wikipedia.org/wiki/Електростатика% 20 сила. Ліцензія: CC BY-SA: Із Зазначенням Авторства
Лоренца сила. Надано: Вікіпедія. Розташовано за адресою: uk.wikipedia.org/wiki/Lorentz_force. Ліцензія: CC BY: Зазначення авторства
Відкритий податковий коледж, Закон Coulombu2019. 25 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m42308/latest/. Ліцензія: CC BY: Зазначення авторства
Джордж Браун, CLF Кілька точкових джерел. 25 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m12747/latest/. Ліцензія: CC BY: Зазначення авторства
Джордж Браун, Закон Кулона. 25 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m12742/latest/. Ліцензія: CC BY: Зазначення авторства
Джордж Браун, CLF Кілька точкових джерел. 26 жовтня 2012 року. Надається: OpenSTAX CNX. Знаходиться за адресою: http://cnx.org/content/m12747/latest/. Ліцензія: CC BY: Зазначення авторства
Закон Кулона. Знаходиться за адресою: http://www.youtube.com/watch?v=Fbyew6sBiOA. Ліцензія: Суспільне надбання: Немає відомих авторських прав. Умови ліцензії: Стандартна ліцензія YouTube