25.1: Системи координат

Системи координат використовуються для опису положення об'єкта в просторі. Система координат - це штучний математичний інструмент, який ми будуємо для того, щоб описати положення реального об'єкта.

1D Системи координат

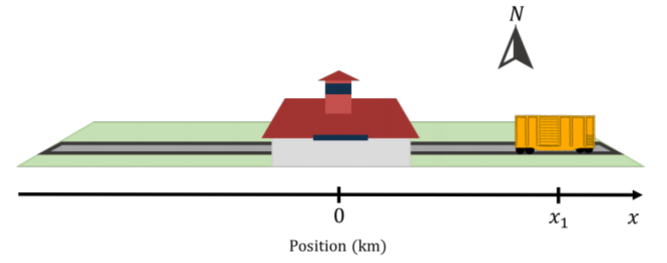
Найпростіша для побудови система координат - це та, яку ми можемо використовувати для опису розташування об'єктів в одновимірному просторі. Наприклад, ми можемо описати розташування поїзда вздовж прямої ділянки колії, що курсує у напрямку Схід-Захід. Для цього ми повинні спочатку визначити «походження», яке є точкою відліку нашої системи координат. Наприклад, походженням для нашої залізничної колії може бути залізнична станція Кінгстона (рис. A1.1.1).

Ми можемо описати положення поїзда, вказавши, як далеко він знаходиться від залізничного вокзалу (походження), використовуючи єдине дійсне число, скажімо\(x\). Якщо поїзд знаходиться на позиції\(x=0\), то ми знаємо, що він знаходиться на станції Кінгстон. Якщо об'єкт не знаходиться в початковій точці, то нам потрібно вміти вказувати, з якого боку (Схід або Захід в нашому прикладі поїзда) походження знаходиться об'єкт. Ми робимо це, вибираючи напрямок для нашої одновимірної координати\(x\). Наприклад, ми можемо вибрати, що східна сторона доріжки відповідає позитивним значенням,\(x\) а західна сторона доріжки відповідає від'ємним значенням\(x\). Таким чином, щоб повністю вказати одновимірну систему координат нам потрібно вибрати:

• місцезнаходження походження.
• напрямок, в якому координата\(x\), збільшується.
• одиниці, в яких ми хочемо висловити\(x\).

В одному вимірі прийнято використовувати змінну\(x\) для визначення положення вздовж «\(x\)-осі». \(x\)-вісь - це наша система координат в одному вимірі, і ми представляємо її, намалювавши лінію зі стрілкою в бік збільшення\(x\) і вказуємо, де знаходиться початок (як на малюнку А1.1.1).

Малюнок A1.1.1: 1d система координат, що описує положення поїзда. Залізнична станція Кінгстон є початком і східна сторона колії відповідає позитивним значенням\(x\). Поїзд розташований на позиції\(x_{1}\).

2D системи координат

Малюнок A1.1.2: Приклад декартової системи координат і точки\(P\) з координатами\((x_{p}, y_{p})\).

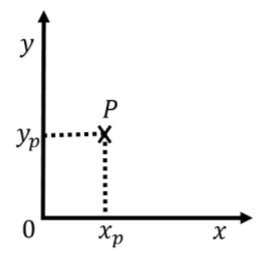
Щоб описати положення об'єкта у двох вимірах (наприклад, мармуровий кочення на столі), нам потрібно вказати два числа. Найпростіший спосіб зробити це - визначити дві\(x\) осі\(y\), походження та напрямок яких ми повинні визначити. На малюнку А1.1.2 показаний приклад такої системи координат. Хоча робити це не обов'язково, ми вибрали\(x\) і\(y\) осі, які перпендикулярні один одному. Походження системи координат - це місце, де дві осі перетинаються. Один може вибрати будь-які два напрямки для осей (до тих пір, поки вони не паралельні). Однак вибір осей, які перпендикулярні («декартова» система координат), як правило, найбільш зручний.

Щоб повністю описати положення об'єкта, ми повинні вказати як його положення по осях, так\(x\) і по\(y\) осях. Наприклад, точка на\(P\) малюнку A1.1.2 має дві координати,\(x_p\) і\(y_p\), які визначають її положення. \(x\)Координата знаходить шляхом проведення лінії\(P\), яка паралельна\(y\) осі і задається перетином цієї лінії з\(x\) віссю. \(y\)Координата знаходить шляхом малювання лінії через точку\(P\), яка паралельна\(x\) осі і задається перетином цієї лінії з\(y\) віссю.

Вправа\(\PageIndex{1}\)

На малюнку A1.1.3 показана система координат, яка не є ортогональною (де\(x\) і\(y\) осі не перпендикулярні). Яке значення на малюнку правильно вказує\(y\) координату точки\(P\)?

Малюнок A1.1.3: Неортогональна система координат (\(x\)і\(y\) осі не перпендикулярні).

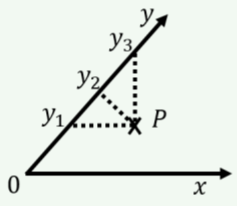
1. \(y_1\)
2. \(y_2\)
3. \(y_3\)

Відповідь

Додайте сюди тексти. Не видаляйте цей текст спочатку.

Найбільш поширеним вибором системи координат у двох вимірах є декартова система координат, яку ми щойно описали, де\(x\)\(y\) осі і перпендикулярні і мають спільне походження, як показано на малюнку A1.1.2. Коли це застосовно, за умовністю, ми зазвичай вибираємо\(y\) вісь, щоб відповідати вертикальному напрямку.

Іншим поширеним вибором є «полярна» система координат, де положення об'єкта задається відстанню до початку\(r\), і кутом\(\theta\), щодо заданого напрямку, як показано на малюнку А1.1.1.4. Часто полярна система координат визначається поряд з декартовою системою, так що\(r\) це відстань до початку декартової системи і\(\theta\) кут по відношенню до\(x\) осі.

Малюнок A1.1.4: Приклад полярної системи координат і точки\(P\) з координатами\((r, θ)\).

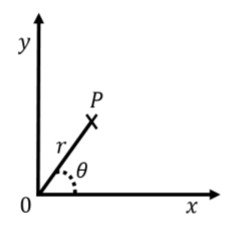
Можна легко конвертувати між двома декартовими координатами\(x\) та\(y\) двома відповідними полярними координатами,\(r\) а також\(\theta\):\[\begin{aligned} x&=r\cos(\theta)\\ y&=r\sin(\theta)\\ r&=\sqrt{x^2+y^2}\\ \tan(\theta) &= \frac{y}{x}\end{aligned}\] Полярні координати часто використовуються для опису руху об'єкта, що рухається навколо circle, так як це означає, що тільки одна з координат (\(\theta\)) змінюється з часом (якщо початок системи координат вибрано так, щоб збігатися з центром кола).

3D Системи координат

У трьох вимірах нам потрібно вказати три числа, щоб описати положення об'єкта (наприклад, птаха, що летить у повітрі). У тривимірній декартовій системі координат ми просто додаємо третю вісь\(z\), тобто взаємно перпендикулярно обом\(x\) і\(y\). Позиція об'єкта може бути визначена за допомогою трьох координат,\(x\),\(y\), і\(z\). За умовністю ми використовуємо\(z\) вісь, щоб бути вертикальним напрямком у трьох вимірах.

Дві додаткові системи координат загальні в трьох вимірах: «циліндричні» і «сферичні» координати. Всі три системи проілюстровані на малюнку А1.1.5, накладеному на декартову систему.

Малюнок A1.1.5: Декартова (зліва), циліндрична (центр) і сферична (права) системи координат, що використовуються в трьох вимірах. \(z\)Осі\(y\) і знаходяться в площині сторінки, тоді як\(x\) вісь виходить зі сторінки.

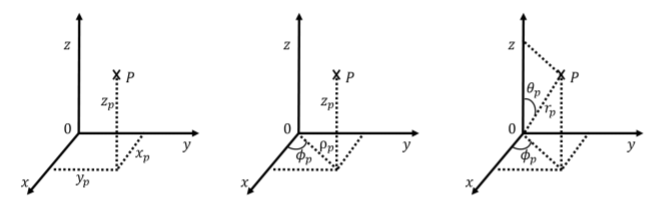
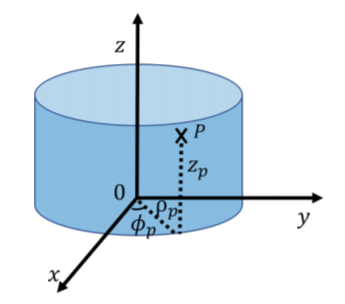
Циліндричні координати можна розглядати як продовження полярних координат. Ми зберігаємо ту ж декартову координату,\(z\) щоб вказати висоту над\(xy\) площиною, однак, ми використовуємо азимутальний кут\(\phi\)\(\rho\), і радіус, щоб описати положення проекції точки на \(xy\)літак. \(\phi\)- кут між\(x\) віссю і лінією від початку до проекції точки в\(xy\) площині і\(\rho\) являє собою відстань між точкою і\(z\) віссю. Таким чином, циліндричні координати дуже схожі на полярну систему координат, введену в двох вимірах, хіба що з додаванням\(z\) координати. Циліндричні координати корисні для опису ситуацій з азимутальною симетрією, таких як рух вздовж поверхні циліндра. Для прикладу розглянемо пункт на\(P\) малюнку А1.1.6. Точка\(P\) розташовується на відстані\(\rho\) від\(z\) осі, так як вона розташована на поверхні циліндра (круглий кінець циліндра має радіус\(\rho\)). Точка\(P\) - це висота\(z\) над\(xy\) площиною, а лінія від\(z\) осі до точки\(P\) робить кут\(\phi\) з\(x\) віссю.

Малюнок А1.1.6: Опис положення\(P\), розташованого на поверхні циліндра, в циліндричних координатах.

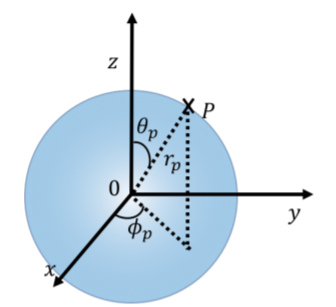
Циліндричні координати пов'язані з декартовими координатами:\[\begin{aligned} \rho &= \sqrt{x^2+y^2}\\ \tan(\phi) &= \frac{y}{x}\\ z&=z\end{aligned}\] У сферичних координатах точка\(P\) описується радіусом\(r\), полярним кутом\(\theta\) та азимутальним кутом, \(\phi\). Радіус - це відстань між точкою і початком. Полярний кут - це кут з\(z\) віссю, який робиться лінією від початку до точки. Азимутальний кут визначається так само, як і в полярних координатах. Зверніть увагу, що значення\(\phi\) має бути між\(0\) і\(2\pi\), тоді як значення\(\theta\) має бути між\(0\) і\(\pi\).

Сферичні координати корисні для опису ситуацій, що мають сферичну симетрію, наприклад людини, що йде по поверхні Землі, так як радіальна координата не зміниться. Наприклад, це показано за допомогою точки на\(P\) малюнку А1.1.1.7, розташованої на поверхні сфери радіуса\(r\).

Малюнок А1.1.7: Опис положення\(P\), розташованої на поверхні сфери, в сферичних координатах.

Сферичні координати пов'язані з декартовими координатами:\[\begin{aligned} r &= \sqrt{x^2+y^2+z^2}\\ \cos(\theta) &= \frac{z}{r}=\frac{z}{\sqrt{x^2+y^2+z^2}}\\ \tan(\phi) &= \frac{y}{x}\\\end{aligned}\]