4.5: Розв'язок рівняння теплопровідності
- Page ID
- 76220
Методи розв'язання рівняння теплопровідності зазвичай наведені в курсах рівнянь з частинними похідними. Тут ми розглянемо простий одновимірний приклад.
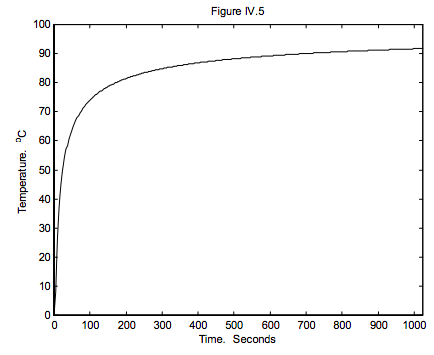
Довгий мідний пруток спочатку при рівномірній температурі 0 о С. В момент часу t = 0, лівий його кінець нагрівають до 100 о С. малюють графіки температури в порівнянні з відстанню х від гарячого кінця планки (до х = 100 см) при t = 4, 16, 64, 256 і 1024 секунди. Намалюйте також графік температури в порівнянні з часом при х = 5 см, до 1024 секунд. Припустимо, що тепло не втрачається з боків планки.
Дані для міді:
К = 400 Вт м −1 К −1
С = 395 Дж, кг −1 К −1
ρ = 8900 кг, м −3
звідки
Д = 1,137 × 10 −4 м 2 с −1
Рівняння, яке потрібно розв'язати,
\[ D \frac{\partial ^2 T}{\partial x^2} = \frac{\partial T}{\partial t}\]
З форми цього рівняння це очевидно (як тільки було вказано!) що можна знайти рішення, в якому T (x, t) є виключно функцією x 2/t, або, з цього приводу, x/t 1/2. Таким чином, нехай
\[ u = x/t^{1/2},\]
і ви побачите, що рівняння 4.4.1 зменшується до загального диференціального рівняння другого порядку
\[ D \frac{d^2T}{du^2} = - \frac{u}{2} \frac{dT}{du}.\]
Нехай T' = dt/du, і це стає ще простіше − рівняння першого порядку:
\[ D \frac{dT'}{du} = - \frac{1}{2} uT'.\]
Після інтеграції ми отримуємо
\[ \ln T' = - \frac{u^2}{4D} + \ln A,\]
де ln A - константа інтеграції, яка визначається початковими і граничними умовами. (Які розміри A?)
Тобто,
\[ T' = A \text{exp} \left[ -u^2 /(4D) \right].\]
Ми повинні знову інтегруватися, стосовно u:
\[ T = A \int \text{exp} \left[ - u^2/(4D) \right] du.\]
Тепер T = 100 o C при x = 0 для будь-якого t > 0. Тобто Т = 100 для u = 0.
І Т = 0 о С при t = 0 для будь-якого х > 0. Тобто T = 0 для u = ∞.
Тому
\[ 100 - 0 = A \int_{ \infty}^0 \text{exp} \left[ -u^2 /(4D) \right] du.\]
Інтеграл трохи важко, хоча добре відомий. Я просто викладу відповідь тут; це так\( - \sqrt{ \pi D}\). З цього ми виявляємо, що константа інтеграції
\[ A = -5284 \text{K m}^{-1} \text{s}^{1/2}.\]
У нас зараз
\[ 100 - T (x,~t) = A \int_{xt^{-1/2}}^0 \text{exp} \left[ -u^2 /(4D) \right] du.\]
Функція помилки erf (r) визначається
\[ \text{erf} (r) = \frac{2}{ \sqrt{ \pi}} \int_0^r \text{exp} (-s^2)ds,\]
так що рівняння 4.4.10 можна записати
\[ T (x,~t) = 100 + A \sqrt{ \pi D} \text{erf} \left( \frac{x}{ 2 \sqrt{Dt}} \right) = 100 \left[ 1 - \text{erf} \left( \frac{x}{2 \sqrt{Dt}} \right) \right].\]
Цю функцію легко побудувати за умови, що ваш комп'ютер дасть вам функцію erf. Розчини показані на малюнках IV.4 і 5.