5.4: Узгодженість
- Page ID
- 78806
У дискусії поки що ми розглядали лише монохроматичне світло, а це означає, що спектр світла складається лише з однієї частоти. Хоча світло від лазера часто має дуже вузьку смугу частот і тому може вважатися монохроматичним, чисто монохроматичного світла не існує. Все світло складається з декількох частот і тому є поліхроматичним. Класичні джерела світла, такі як лампи розжарювання, а також світлодіоди мають відносно широкі смуги частот. Тоді виникає питання, як по-різному поводиться поліхроматичне світло порівняно з ідеалізованим випадком монохроматичного світла. Щоб відповісти на це питання, треба вивчити тему узгодженості. Розрізняють дві крайності: повністю когерентний і повністю некогерентний світло, тоді як ступінь узгодженості практичного світла знаходиться десь посередині. Взагалі кажучи, чим ширше смуга частот джерела, тим некогерентніше світло. Це дуже важливе спостереження, що жодне світло насправді не є повністю узгодженим або повністю незв'язним. Все світло частково узгоджене, але деяке світло є більш зв'язним, ніж інші.
Інтуїтивно зрозумілий спосіб думати про ці поняття полягає в здатності формувати інтерференційні смуги. Наприклад, при лазерному світлі, який зазвичай майже монохроматичний і, отже, когерентний, можна сформувати інтерференційну картину з чіткими максимумами та мінімумами інтенсивності (так звані бахроми) за допомогою подвійної щілини, тоді як з сонячним світлом (що некогерентно) це набагато складніше. Кожна частота в спектрі сонячного світла дає свою власну інтерференційну картину зі своєю частотою залежною схемою бахроми. Ці візерунки бахроми вимиваються через суперпозицію та загальну інтенсивність, тому демонструють невеликий контраст бахроми, тобто узгодженість менше. Однак створити інтерференційні бахроми природним освітленням не можна. Хитрість полягає в тому, щоб дозволити двом щілинам бути настільки близько один до одного (порядку\(0.02 \mathrm{~mm}\)), що різниця у відстанях від щілин до сонця настільки мала, щоб поля в щілині були досить узгодженими, щоб заважати. Щоб зрозуміти вплив поліхроматичного світла, важливо розуміти, що ступінь, до якої поля в двох точках є когерентними, тобто здатність утворювати смуги, визначається різницею відстаней між цими точками та джерелом. Сама відстань до джерела не має значення. У наступних розділах ми вивчаємо ці питання більш кількісно.
5.3.1 Узгодженість джерел світла
У звичайному джерелі світла, такому як газорозрядна лампа, фотони генеруються електронними переходами в атомах газу. Ці переходи мають тривалість порядку\(10^{-8}\) до\(10^{-9} \mathrm{~s}\). Оскільки випромінювані хвильові поїзди є кінцевими, випромінюване світло не має однієї частоти; натомість існує смуга частот навколо центральної частоти. Такий розкид частот називається природною шириною лінії. Випадкові теплові рухи молекул викликають подальше розширення за рахунок ефекту Доплера. Крім того, атоми зазнають зіткнень, які переривають хвильові поїзди і, отже, ще більше розширюють частотний спектр.
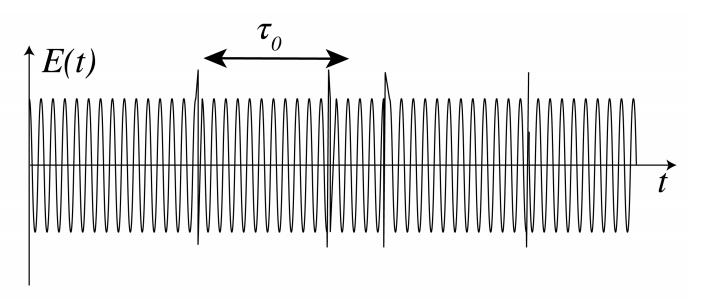
Розглянемо спочатку один випромінюючий атом. Коли зіткнення є домінуючим ефектом розширення, і ці зіткнення досить короткі, так що будь-яке випромінювання, що випромінюється під час зіткнення, може бути проігноровано, точною моделлю для випромінюваної хвилі є стійкий монохроматичний хвильовий поїзд\(\bar{\omega}\) на частоті в центрі смуги частот, переривається випадковими фазовими стрибками кожного разу, коли відбувається зіткнення. Розриви у фазі через зіткнення викликають поширення частот навколо центральної частоти. Приклад наведено на рис\(\PageIndex{1}\). Середній час\(\tau_{0}\) між зіткненнями зазвичай становить менше 10 нс, що означає, що в середньому між двома зіткненнями відбувається приблизно 150 000 гармонічних коливань. Час когерентності\(\Delta \tau_{c}\) визначається як максимальний проміжок часу, протягом якого можна передбачити фазу електричного поля. У разі зіткнень, що переважають викиди одним атомом, час когерентності дорівнює середньому часу між наступними зіткненнями:\(\Delta \tau_{c}=\tau_{0}\).
Щоб зрозуміти когерентність та некогерентність, дуже корисно використовувати цю модель для випромінювання одним атомом як гармонічні хвильові поїзди тисяч періодів, перервані випадковими фазовими стрибками. Час когерентності і ширина\(\Delta \omega\) частотної лінії пов'язані як
\[\Delta \tau_{c}=\frac{2 \pi}{\Delta \omega} \nonumber \]
Довжина когерентності визначається\[\Delta \ell_{c}=c \Delta \tau_{c} . \nonumber \]
З тих пір\(\lambda \omega=2 \pi c\), у нас\(\bar{\omega}\) є\[\frac{\Delta \lambda}{\bar{\lambda}}=\frac{\Delta \omega}{\bar{\omega}}, \nonumber \] де\(\lambda\) і є довжина хвилі і частота в центрі лінії. Отже,\[\Delta \ell_{c}=c \frac{2 \pi}{\Delta \omega}=2 \pi \frac{c}{\bar{\omega}} \frac{\bar{\omega}}{\Delta \omega}=\frac{\bar{\lambda}^{2}}{\Delta \lambda} \nonumber \]
Довжина когерентності і час узгодженості ряду джерел наведені в табл\(\PageIndex{1}\).
| Джерело | Середня довжина хвилі | Ширина лінії | Довжина когерентності | Час узгодженості |
|---|---|---|---|---|
| \(\bar{\lambda}\) | \(\Delta \lambda\) | \(\bar{\lambda}^{2} / \Delta \lambda\) | \(\frac{\bar{\lambda}}{\Delta \lambda} \frac{\bar{\lambda}}{c}\) | |
| Середній ІК (3-5\(\mu \mathrm{m}\)) | \(4.0 \mu \mathrm{m}\) | \(2.0 \mu \mathrm{m}\) | \(8.0 \mu \mathrm{m}\) | \(2.66 \times 10^{-14} \mathrm{~s}\) |
| Біле світло | \(550 \mathrm{~nm}\) | \(\approx 300 \mathrm{~nm}\) | \(\approx 900 \mathrm{~nm}\) | \(\approx 3.0 \times 10^{-14} \mathrm{~s} .\) |
| Меркурій дуги | \(546.1 \mathrm{~nm}\) | \(\approx 1.0 \mathrm{~nm}\) | \(\approx 0.3 \mathrm{~mm}\) | \(\approx 1.0 \times 10^{-12} \mathrm{~s} .\) |
| Kr\(^{86}\) розрядна лампа | \(605.6 \mathrm{~nm}\) | \(1.2 \times 10^{-3} \mathrm{~nm}\) | \(0.3 \mathrm{~m}\) | \(1.0 \times 10^{-9} \mathrm{~s} .\) |
| Стабілізований лазер He-Ne | \(632.8 \mathrm{~nm}\) | \(\approx 10^{-6} \mathrm{~nm}\) | \(400 \mathrm{~m}\) | \(1.33 \times 10^{-6}\)с. |
5.3.2 Поліхроматичне світло
При роботі з когерентністю потрібно враховувати поля, які складаються з діапазону різних частот. \(\mathcal{U}(\mathbf{r}, t)\)Дозволяти бути реальною фізичною складовою поля. Завжди можна записати\(\mathcal{U}(\mathbf{r}, t)\) як інтеграл над часово-гармонійними складовими:\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} \int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega, \nonumber \] де\(A_{\omega}(r)\) - комплексна амплітуда часово-гармонічного поля з частотою\(\omega\). Коли є лише певна смуга частот, яка сприяє, то\(A_{\omega}=0\) для\(\omega\) поза цією смугою. Визначимо комплексне залежне від часу поле\(U(\mathbf{r}, t)\) за\[U(\mathbf{r}, t)=\int_{0}^{\infty} A_{\omega}(\mathbf{r}) e^{-i \omega t} \mathrm{~d} \omega . \nonumber \]
Тоді\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t) \nonumber \]
Примітка: Комплексне поле тепер\(U(\mathbf{r}, t)\) містить залежність від часу на відміну від позначення, використовуваного для часово-гармонічного (тобто одночастотного) поля, введеного в главі 2, де залежне від часу\(e^{-i \omega t}\) було окремим фактором.
Квазімонохроматичне поле. Якщо ширина\(\Delta \omega\) смуги частот дуже вузька, ми говоримо про квазімонохроматичному польоті. При поширенні квазімонохроматичних полів використано формулу часово-гармонічних полів на центральній частоті\(\bar{\omega}\). Квазімонохроматичне припущення значно спрощує обчислення. Тим не менш, більша частина лікування, яка слідує, є більш загальною і не передбачає, що поле квазімонохроматичне.
Зараз ми обчислюємо інтенсивність поліхроматичного світла. Миттєвий потік енергії (як для монохроматичного світла) пропорційний квадрату миттєвого реального поля:\(\mathcal{U}(\mathbf{r}, t)^{2}\). Ми усереднюємо миттєву інтенсивність за час\(T\) інтеграції загальних детекторів, яка, як зазначено раніше, дуже довга порівняно з періодом на центральній\(2 \pi / \bar{\omega}\) частоті поля (принаймні,\(10^{5}\) раз за період світла). Використовуючи визначення (5.2.6) і\[\mathcal{U}(\mathbf{r}, t)=\operatorname{Re} U(\mathbf{r}, t)=\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right) / 2, \nonumber \] ми отримуємо,\[\begin{aligned} \left\langle\mathcal{U}(\mathbf{r}, t)^{2}\right\rangle &=\frac{1}{4}\left\langle\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\left(U(\mathbf{r}, t)+U(\mathbf{r}, t)^{*}\right)\right\rangle \\ &=\frac{1}{4}\left\{\left\langle U(\mathbf{r}, t)^{2}\right\rangle+\left\langle\left(U(\mathbf{r}, t)^{*}\right)^{2}\right\rangle+2\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle\right\} \\ &=\frac{1}{2}\left\langle U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\right\rangle \\ &=\frac{1}{2}\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \end{aligned} \nonumber \] де середні значення\(U(\mathbf{r}, t)^{2}\) і\(\left(U(\mathbf{r}, t)^{*}\right)^{2}\) дорівнюють нулю, оскільки вони є швидкоколивальними функціями часу. На відміну від цього,\(|U(\mathbf{r}, t)|^{2}=U(\mathbf{r}, t)^{*} U(\mathbf{r}, t)\) має DC-компонент, який не в середньому дорівнює нулю.
Зауваження: На відміну від часово-гармонічного випадку, середній показник поліхроматичного світла залежить від часу,\(t\) в який береться середнє значення. Однак ми припускаємо в цьому розділі, що поля опускаються джерелами, які є стаціонарними. Властивість стаціонарності має на увазі, що середнє за часовий проміжок великої довжини\(T\) не залежить від часу, за який береться середнє значення. Багато джерел світла, зокрема звичайні лазери, є стаціонарними. (Однак лазерне джерело, яке випромінює короткі потужні імпульси, не можна розглядати як стаціонарне джерело). Крім того, ми припускаємо, що поля є ергодичними, що означає, що прийняття середнього часу протягом тривалого часового інтервалу дорівнює тому ж, що приймати середнє за ансамблем можливих полів. Можна показати, що ця властивість означає, що межа\(T \rightarrow \infty\) в (5.2.6) дійсно існує.
Для інтенсивності знову використовується вираз без\(1 / 2\) коефіцієнта попереду, тобто\[I(\mathbf{r})=\left\langle|U(\mathbf{r}, t)|^{2}\right\rangle . \nonumber \] усереднена за часом інтенсивність виражається через середню за часом квадратного модуля комплексного поля.