1.10: Відображення та передача на інтерфейсі

Коли електромагнітне поле падає на межі розділу між різними середовищами, поле частково відбивається і частково передається. Важливим особливим випадком є монохроматична плоска хвиля, яка падає на плоский інтерфейс, як на малюнку\(\PageIndex{2}\).

Нехай інтерфейс буде площиною\(z = 0\) між матеріалами в\(z < 0\) і\(z > 0\) з діелектричними можливостями\(E_i\) і\(E_t\), відповідно. Спочатку ми припускаємо, що матеріали без втрат, тобто що діелектричні дозволи реальні. Плоска хвиля падає із середовища,\(z < 0\) а падаюче електромагнітне поле задається:

\[ \begin{align} ε^i(r, t) &= Re [ ε^i(r)e^{−iωt}] \\[4pt] &= Re \left[ A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

і

\[\begin{align} H^i(r, t) &= Re [ H^i(r)e^{−iωt}] \\[4pt] &= Re \left[ \dfrac{k^i}{ωµ_{0}} × A^ie^{i(k^{i}·r−ωt)}\right] \end{align} \nonumber \]

де k ⁱ = k ⁱ _х х + k ⁱ _y y + k ⁱ _z z, з

\[k_{z}^i=(k_{0}^2E_{i} − (k_{x}^i)^2 − (k_{y}^i)^2)^{1/2}. \nonumber \]

Оскільки залежність від часу задається\(\exp(−iωt)\) з,\(ω > 0\) а падаюча хвиля поширюється в додатному z-напрямку, позитивний квадратний корінь вибирається для k ⁱ _z. Частина поля інциденту відбивається в\(z < 0\) і частина передається в\(z > 0\). Відображене поле пишеться як

\[ε^r(r, t) = Re [ ε^r(r)e^{−iωt}] = Re [ A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

\[H^r(r, t) = Re [ H^r(r)e^{−iωt}] = Re [ \dfrac{k^r}{ωµ_{0}} × A^re^{i(k^{r}·r−ωt)}] , \nonumber \]

де k ^р = к ^р _х х + к _^р у +к ^р _з з, з

\[k_{z}^r=(k_{0}^2E_{i} − (k_{x}^r)^2 − (k_{y}^r)^2)^{1/2}, \nonumber \]

де обраний знак мінус, оскільки відбита хвиля поширюється в негативному z-напрямку. Передане поле призначене для\(z > 0\)

\[ε^t(r, t) = Re [ ε^t(r)e^{−iωt}] = Re [ A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

\[H^t(r, t) = Re [ H^t(r)e^{−iωt}] = Re [ \dfrac{k^t}{ωµ_{0}} × A^te^{i(k^{t}·r−ωt)}] , \nonumber \]

_{де k ^т = к ^т х х + к ^т у + к ^т з з, з}

\[k_{z}^t=(k_{0}^2E_{i} − (k_{x}^t)^2 − (k_{y}^t)^2)^{1/2}. \nonumber \]

Наша мета полягає в тому, щоб визначити A ^r і A ^t для заданого A ⁱ.

1.9.1 Граничні умови на інтерфейсі

Існують умови безперервності тангенціальної і нормальної складових як електричного, так і магнітного полів на межі розділу між різними середовищами. Граничні умови для тангенціальних складових випливають з рівнянь Максвелла, які містять curl-оператор, тобто (1.6.2) і (1.6.3). Там тримає для інтерфейсу z = 0 з падаючими, відбитими і переданими площинами хвилями, введені вище:

\[\hat{z} × (E^i + E^r ) = \hat{z} × E^t, \nonumber \]

\[\hat{z} × (H^i + H^r ) = \hat{z} × H^t, \nonumber \]

де z - одиниця нормальної на інтерфейсі. Це означає, що тангенціальні компоненти загального електричного та загального магнітного поля безперервні через інтерфейс, або явно:

\[E_{x}^i(x, y, 0) + E_{x}^r(x, y, 0) = E_{x}^t(x, y, 0), \nonumber \]

\[E_{y}^i(x, y, 0) + E_{y}^r(x, y, 0) = E_{y}^t(x, y, 0), \nonumber \]

і аналогічно для магнітного поля.

Малюнок\(\PageIndex{1}\): Замкнутий контур у (x, z) -площині, що охоплює область A та навколишню частину інтерфейсу z = 0, як використовується в законі Стокса для отримання безперервності електричних та магнітних компонентів, які є тангенціальними до інтерфейсу та паралельні площині через петлю.

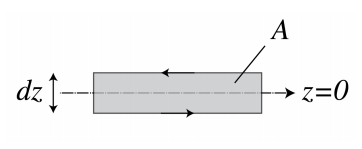
Ми лише продемонструємо безперервність тангенціальних складових для електричного поля. Вибравши замкнутий контур в (x, z) -площині, який перетинається інтерфейсом z = 0, як показано на малюнку\(\PageIndex{1}\), і інтегруючи y-складову Закону Фарадея (1.3.12) для загального електромагнітного поля над площею A, обмеженою контуром L, отримаємо:

\[-µ_{0}\dfrac{d}{dt}\iint\limits_{A} \hat{y}H\, dA=\iint\limits_{A} \hat{y}∇ × ε\, dA=\oint\limits_{L} ε\, dl \nonumber \]

де на останньому кроці ми використовували теорему Стокса з напрямком інтеграції через петлю, заданий напрямком обертання шуруповерта, коли вона рухається у напрямку нормального y. У словах: швидкість зміни магнітного потоку через поверхню А дорівнює інтегралу тангенціального електричного поля над обмежуючим замкнутим контуром Л.

Прийнявши межу dz → 0, поверхневий інтеграл і інтеграли над вертикальними частинами петлі зникають і залишаються тільки інтеграли тангенціального електричного поля над горизонтальними частинами петлі по обидва боки розділу z = 0. Оскільки ці інтеграли пройдені в протилежних напрямках і довжини цих частин однакові і довільні, ми робимо висновок для циклу, як показано на малюнку\(\PageIndex{1}\), що

\[lim_{z↑0} ε_{x}(x, y, z, t) = lim_{z↓0} ε_{x}(x, y, z, t), \nonumber \]

де ε - сумарне електричне поле, тобто воно дорівнює сумі падаючого і відбитого поля для z < 0, and equal to the transmitted field in z > 0. Вибираючи замкнутий контур у (y, z) -площині замість (x, z) -площині, можна знайти аналогічно тому, що y-складова електричного поля є безперервною. Неперервність тангенціальних складових магнітного поля виведені аналогічним чином.

Наша деривація призначена для електромагнітних полів довільної залежності від часу. Крім того, похідні, використані вище для плоского інтерфейсу z = 0, можуть бути легко узагальнені для криволінійних поверхонь. Тому робимо висновок:

Тангенціальні електричні та магнітні компоненти поля безперервні через будь-який інтерфейс.

Інтегруючи рівняння Максвелла, що містять div-оператор (1.3.14), (1.3.15) над таблеткою з висотою dz і верхньою і нижньою поверхнями з обох боків і паралельно інтерфейсу, і враховуючи граничну dz → 0, ми знаходимо співвідношення неперервності для нормальних складових полів:

\[lim_{z↑0} E_{i}\hat{z}ε_{x}(x, y, z, t) = lim_{z↓0} E_{t}\hat{z}εx(x, y, z, t), \nonumber \]

\[lim_{z↑0} H_{x}(x, y, z, t) = lim_{z↓0} H_{x}(x, y, z, t), \nonumber \]

Нормальні компоненти E ε і H є безперервними через інтерфейс.

Зауваження

Оскільки всі похідні граничні умови тримаються за всі часи t, випливає, що для часових гармонічних полів вони також утримуються для складних полів. Звідси (\(\PageIndex{10}\)) і (\(\PageIndex{11}\)) hold і аналогічно ми знаходимо, що нормальні компоненти E ε і H є безперервними.

1.9.2 Закон Снелла

Підставивши складні електричні поля, отримані з (\(\PageIndex{1}\)), (\(\PageIndex{4}\)) і (\(\PageIndex{7}\)) в рівняння (\(\PageIndex{10}\)), отримаємо

\[\hat{z} × [A^ie^{i(k_{x}^{i}·x+k_{y}^{i}·y)}+A^re^{i(k_{x}^{r}·x+k_{y}^{r}·y)}]=\hat{z} × A^te^{i(k_{x}^{t}·x+k_{y}^{t}·y)}, \nonumber \]

Так як це рівняння має бути виконано для всіх точок (x, y), з цього випливає, що

\[k_{x}^{i}=k_{x}^{r}=k_{x}^{t}, \nonumber \]

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}, \nonumber \]

Значить, тангенціальні складові хвильових векторів падаючих, відбитих і переданих хвиль ідентичні. Насправді, якщо (\(\PageIndex{19}\)) не буде утримувати, то, зберігаючи y фіксованим, експоненціальні функції in (\(\PageIndex{18}\)) не всі мали б однакову періодичність, як функції x, а потім (\(\PageIndex{18}\)) ніколи не могли бути задоволені для всіх х. Той самий аргумент з x зберігається фіксованим призводить до висновку (\(\PageIndex{20}\)).

Не обмежуючи загальність, ми відтепер будемо вважати, що система координат обрана така, що

\[k_{y}^{i}=k_{y}^{r}=k_{y}^{t}=0. \nonumber \]

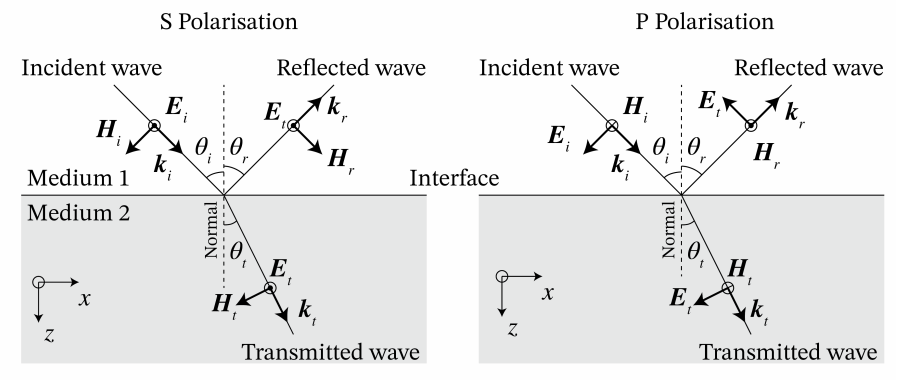
Площина через вектор падаючої хвилі і нормаль до розділу називається площиною падіння. Отже, у випадку з (\(\PageIndex{21}\)) площиною падіння є (x, z) -площина.

Так як довжина хвильових векторів ki і kr дорівнює k ₀ n _i, при k ₀ число хвиль у вакуумі і n _i = (E _i /E ₀) ^1/2 показник заломлення, а так як довжина kt дорівнює k ₀ n _t, з n _t = (_Е т/Е ₀) ^1/2, випливає з (\(\PageIndex{19}\))

\[sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}n_{i}}=\dfrac{k_{x}^{r}}{k_{0}n_{r}}=sin θ_{r}, \nonumber \]

і

\[n_{i}sin θ_{i} = \dfrac{k_{x}^{i}}{k_{0}}=\dfrac{k_{x}^{t}}{k_{0}}=n_{t}sin θ_{t}, \nonumber \]

де кути такі, як на рис\(\PageIndex{2}\). Отже,

\[θ_{i} = θ_{r}, angle\space of\space reflection = angle\space of\space incidence, \nonumber \]

\[n_{i}sin θ_{i} =n_{t}sin θ_{t},Snell’s\space Law . \nonumber \]

Закон Снелла передбачає, що при збільшенні кута падіння θ _i кут передачі збільшується також. Якщо середовище в z < 0 - повітря з показником заломлення n _i = 1, а інше середовище - скло з показником заломлення n _t = 1,5, то максимальний кут пропускання виникає при θ _i = 90 ^o с

\[θ_{t,max} = arcsin(n_{i}/n_{t}) = 41.8^o. \nonumber \]

Рисунок\(\PageIndex{2}\): Вектори падаючих, відбитих та переданих хвиль з електричними та магнітними векторами для s- та p-поляризації. Для s-поляризації електричне поле вказує на площину в той момент, коли для p-поляризації магнітне поле вказує на площину в показаний момент.

У випадку, якщо світло падає зі скла, тобто n _i = 1,5 і n _t = 1,0, кут падіння θ _i не може бути більшим за 41,8 ^o, оскільки в іншому випадку для θ _t немає реального рішення. Виявляється, коли θ _i > 41.8 ^o, хвиля повністю відбивається і в повітрі відсутня поширюється передається хвиля. Як пояснено в розділі 1.9.5, це, однак, не означає, що в z > 0 немає поля. Насправді існує не поширюється так звана еванесентна хвиля в z > 0. Кут θ _{i, crit} = 41.8 ^o називається критичним кутом повного внутрішнього відображення. Він існує лише в тому випадку, якщо хвиля падає із середовища з більшим показником заломлення на середовище з меншим показником заломлення (n _t < n _i). Критичний кут не залежить від поляризації падаючої хвилі.

1.9.3 Коефіцієнти Френеля

Через (\(\PageIndex{19}\)) і (\(\PageIndex{21}\)) записуємо k _x = k ⁱ _x = k ^r _x = k ^t _x і тому k ⁱ _z = (k ² ₀ E _i − k ² _x) ^1/2 = −к ^р _з і k ^т _з = (k ² ₀ E _t − k ² _х) ^1/2. Отже,

\[k^i = k_{x}\hat{x} + k^i_{z}\hat{z}, k^r = k_{x}\hat{x} − k^i_{z}\hat{z}, \nonumber \]

і

\[k^t =k_{x}\hat{x} − k^t_{z}\hat{z}, \nonumber \]

Згідно (1.6.11), для падаючих, відбитих і переданих плоских хвиль там повинні утримуватися:

\[A^i · k^i = A^r · k^r = A^t · k^t = 0. \nonumber \]

Обираємо ортонормальну базису, перпендикулярну k ⁱ з одиничними векторами:

\[\hat{s}= \hat{y} , \hat{p}^i=\dfrac{1}{|k^i|}(-k_{z}^i\hat{x}+k_{x}\hat{z}), \nonumber \]

де

\[|k^i|= (k^i · (k^i)^*)^{1/2}=(k_{x}^2 · |k_{z}^i|^2)^{1/2}, \nonumber \]

і де в письмовій формі складний кон'югат ми передбачаємо випадок k ⁱ _z є складним, що може статися, наприклад, коли E _i є складним (випадок, який був виключений до цих пір, але який пізніше буде розглянуто) або у випадку хвиль, що зникають, обговорюється в розділі 1.9.5. Зверніть увагу, що коли k ⁱ _z є дійсним, |k _i | = (k ² _x + (k ⁱ _z) _²) ^1/2 = k0ni. Неважко помітити, що базису (\(\PageIndex{30}\)) є ортонормальним у просторі двовимірних комплексних векторів і що s · k ⁱ = p ⁱ · k ⁱ = 0. Вектор s перпендикулярний площині падіння, тому складова електричного поля в цьому напрямку поляризується перпендикулярно площині падіння і називається s-поляризованою (німецькою мовою «Senkrecht»). Інший базисний вектор p ⁱ (для дійсних k ⁱ) паралельний площині падіння і коли електрична складова в цьому напрямку називається p-поляризованою. Складний вектор A ⁱ можна розширити за такою ознакою:

\[A^i = A^i_{s} \hat{y} + A^i_{p} \hat{p}^i. \nonumber \]

Так як

\[k^i × \hat{y} = |k^i|\hat{p}^i, k^i × \hat{p}^i =-\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

з цього випливає, що електричне і магнітне поле падаючої площини хвилі можна записати як

\[E^i(r) =(A^i_{s} \hat{y} + A^i_{p} \hat{p}^i)e^{ik^i·r}, \nonumber \]

\[H^i(r) = (\dfrac{|k^i|}{ωµ_{0}}A^i_{s}\hat{p}^i-\dfrac{ωE_{0}E_{i}}{|k^i|}A^i_{p}\hat{y})e^{ik^i·r}. \nonumber \]

Відбите поле розширюється на основі y і p ^r с

\[\hat{p}^r=-\dfrac{1}{|k^i|}(k^i_{z}\hat{x}+k_{x}\hat{z}). \nonumber \]

Знак перед одиничним вектором p ^r вибирається таким чином, щоб його x-складова була такою ж, як у p ⁱ. Так як

\[k^r × \hat{y} = -|k^i|\hat{p}^r, k^r × \hat{p}^r =\dfrac{k^2_{0}E_{i}}{|k^i|}\hat{y}, \nonumber \]

з цього випливає, що

\[E^r(r) =(A^r_{s} \hat{y} + A^r_{p} \hat{p}^r)e^{ik^r·r}, \nonumber \]

\[H^r(r) = (-\dfrac{|k^i|}{ωµ_{0}}A^r_{s}\hat{p}^r+\dfrac{ωE_{0}E_{i}}{|k^i|}A^r_{p}\hat{y})e^{ik^r·r}, \nonumber \]

де ми використовували, що k ^{r · k r} = k ₀ ² n _i ² і |k ^r | = (k _x ² + |k _z ^r | ²) ^1/2 = (k _x ² + |k _z ⁱ | ²) ^1/2 = |к ^я |. Для переданої плоской хвилі використовуємо основу y і p ^t с

\[\hat{p}^t=\dfrac{1}{|k^t|}(-k^t_{z}\hat{x}+k_{x}\hat{z}), \nonumber \]

де p ^t вибирається таким чином, що х-компонент p ^t має той же знак, що і x-компонент p ⁱ. Так як

\[k^t × \hat{y} = |k^t|\hat{p}^t, k^t × \hat{p}^t =\dfrac{k^2_{0}E_{t}}{|k^t|}\hat{y}, \nonumber \]

отримуємо

\[E^t(r) =(A^t_{s} \hat{y} + A^t_{p} \hat{p}^t)e^{ik^t·r}, \nonumber \]

\[H^t(r) = (\dfrac{|k^t|}{ωµ_{0}}A^t_{s}\hat{p}^t-\dfrac{ωE_{0}E_{i}}{|k^t|}A^t_{p}\hat{y})e^{ik^t·r}, \nonumber \]

Тепер ми розглянемо s-поляризовану хвилю падаючої площини, тобто A _p ⁱ = 0. Ми покажемо, що всі граничні умови можуть бути задоволені A _p ^r = A _p ^t = 0 і шляхом відповідного вираження A _{s ^r і A s} ^t через A _s ⁱ. Це означає, що якщо падаюча плоска хвиля s-поляризована, відбиті та передані хвилі також s-поляризуються. Для s-поляризації електричне поле має лише y-компонент і цей компонент є тангенціальним до інтерфейсу z = 0. Це призводить до стану

\[A^i_{s}+A^r_{s}=A^t_{s}. \nonumber \]

Єдиною тангенціальною складовою магнітного поля є x-складова і вимагає, щоб вона була безперервною для z = 0 призводить до

\[-k^i_{z}A^i_{s}+k^i_{z}A^r_{s}=-k^t_{z}A^t_{s}. \nonumber \]

Розв'язування (\(\PageIndex{44}\)), (\(\PageIndex{45}\)) для A _s ^r і A _s ^t дає наступну формулу коефіцієнтів відображення і пропускання:

\[r_{s}=\dfrac{ A^r_{s} }{ A^i_{s} }=\dfrac{ k^i_{z} -k^t_{z} }{k^i_{z} +A^t_{z} }, \nonumber \]

\[t_{s}=\dfrac{ A^t_{s} }{ A^i_{s} }=\dfrac{ 2k^i_{z} }{k^i_{z} +A^t_{z} }. \nonumber \]

Тільки магнітне поле має z-складову і легко перевірити, що H _z ⁱ + H _z ^r = H _z для z = 0.

Дивлячись на випадок p-поляризованої падаючої хвилі: A _s ⁱ = 0, ми бачимо, що вираз для магнітного поля в p-поляризованому випадку стає подібним (крім обраних знаків) до виразу електричного поля для s-поляризації і навпаки. Забезпечення неперервності тангенціальних компонентів при z = 0 дає p-поляризацію:

\[r_{p}=\dfrac{ A^r_{p} }{ A^i_{p} }=-\dfrac{ \dfrac{k^i_{p}}{E_{i}} -\dfrac{k^t_{p}}{E_{t}}}{\dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}}} , \nonumber \]

\[t_{p}=\dfrac{ A^t_{p} }{ A^i_{p} }=\dfrac{ 2 \dfrac{k^i_{p}}{E_{i}} }{ \dfrac{k^i_{p}}{E_{i}} +\dfrac{k^t_{p}}{E_{t}} }. \nonumber \]

Легко перевірити, що E _z є єдиною нормальною складовою і що e _i (E _z ⁱ + E _z ^r) = e _t E _z ^t для z = 0.

Коефіцієнти відбиття і пропускання r _s, r _p, t _s і tp називаються коефіцієнтами Френеля. Як випливає з деривації, немає перехресних розмов між s- та p-поляризованими площинними хвилями, що падають на плоский інтерфейс. Загальнополяризовану хвилю падаючої площини завжди можна записати як лінійну комбінацію s- та p-поляризованих хвиль падаючої площини. Оскільки загалом r _s ≠ r _p і t _s ≠ t _p випливає, що відбиті і передані поля також є лінійними комбінаціями s- і p-поляризованих полів, але з різними коефіцієнтами (вагами) цих двох фундаментальних станів поляризації, ніж для падаюча хвиля.

Зауваження.

1. При виведенні коефіцієнтів Френеля безперервність нормальних компонентів поля не використовувалася і виконувалася автоматично. Причина полягає в тому, що електромагнітні поля плоских хвиль вибираються перпендикулярно хвильовим векторам. Це означає, що розбіжність E ε і H зникає, що в свою чергу означає, що нормальні компоненти автоматично безперервні по інтерфейсу.

2. Коли kiz і ktz обидва дійсні, ми маємо |k ⁱ | = k ₀ n _i і |k ^t | = k ₀ n _t і коефіцієнти Френеля можуть бути виражені в кутах θ _i, θ _r і θ _t і показниках заломлення n _i = _{Е я ^1/2 /Е 0 і п т = (Е т/Е 0) ^1/2.} Оскільки k _z ⁱ = k ₀ n _i cos θ _i і k _z ^t = k ₀ n _t cos θ _t, знаходимо

\[r_{s}=\dfrac{n_{i}cosθ_{i}-n_{t}cosθ_{t}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=-\dfrac{sin(θ_{i}-θ_{t})}{sin(θ_{i}+θ_{t})}, \nonumber \]

\[t_{s}=\dfrac{2n_{i}cosθ_{i}}{n_{i}cosθ_{i}+n_{t}cosθ_{t}}=\dfrac{2cosθ_{i}sinθ_{t}}{sin(θ_{i}+θ_{t})}, \nonumber \]

і

\[r_{p}=-\dfrac{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}}}{ \dfrac{cosθ_{i}}{n_{i}}- \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{tan(θ_{i}-θ_{t})}{tan(θ_{i}+θ_{t})}, \nonumber \]

\[t_{p}=\dfrac{\dfrac{2cosθ_{i}}{n_{i}}}{ \dfrac{cosθ_{i}}{n_{i}}+ \dfrac{cosθ_{t}}{n_{t}} }=-\dfrac{ 2cosθ_{i}sinθ_{t} }{tan(θ_{i}+θ_{t})}. \nonumber \]

Для отримання виразів на крайньому правому краю в (\(\PageIndex{50}\)), (\(\PageIndex{51}\)), (\(\PageIndex{52}\)) і (\(\PageIndex{53}\)) Закон Снелла був використаний.

3. Перевага виразів (\(\PageIndex{46}\)), (), (\(\PageIndex{47}\)), (\(\PageIndex{48}\)\(\PageIndex{49}\)) в терміні компонентів хвильового вектора kiz і ktz полягає в тому, що вони також застосовуються, коли k _z ⁱ та/або k _z ^t є складними. Це відбувається, наприклад, коли є поглинання в z < 0 or in z > 0 або обох, або коли E _i > E _t і кут падіння вище критичного кута, через що k _z ^t є чисто уявним (див. Розділ 1.9.5).

Рисунок\(\PageIndex{3}\): Коефіцієнти відбиття та пропускання як функція кута падіння s- та p-поляризованих хвиль, що падають з повітря на скло. Вказується кут Брюстера θ _B.

1.9.4 Властивості коефіцієнтів Френеля

Для нормальної захворюваності: θ _i = 0, Закон Снелла має на увазі: θ _t = 0. Отже, (\(\PageIndex{50}\)), (\(\PageIndex{52}\)) дають:

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{n_{i}-n_{t}}{n_{i}+n_{t}}, \nonumber \]

Видно, що для нормальної захворюваності r _p = r _s, як і очікувалося. Однак зауважте, що якби ми не визначили p ^_r таким чином, що його тангенціальна складова така ж, як у p ⁱ, два коефіцієнти відбиття мали б протилежний знак для нормальної частоти (як це відбувається в деяких книгах). Якщо падаюче середовище повітря, а інше середовище - скло (n _i = 1,0, n _t = 1,5), отримуємо

\[r_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=-0.2, \nonumber \]

а так як потік енергії пропорційний квадрату поля, то з цього випливає, що 4% нормального падаючого світла відбивається склом. Звідси лінза зі скла без антивідблиску покриття відбиває приблизно 4% світла при нормальному падінні. Коефіцієнт пропускання при нормальному падінні становить:

\[t_{s}(θ_{i}=0)=r_{p}(θ_{i}=0)=\dfrac{2n_{i}}{n_{i}+n_{t}}, \nonumber \]

який для повітряного скла стає 0,8.

Зауваження. Енергозбереження вимагає, щоб нормальна < Sz > складова усередненого за часом потоку енергії через інтерфейс була безперервною. Використовуючи формулу для усередненого за часом вектора Пойнтінга плоской хвилі (1.8.8), можна перевірити, що коефіцієнти Френеля такі, що потік енергії дійсно безперервний.

З Закону Снелла (\(\PageIndex{25}\)) випливає, що sin θ _t = (n _i /n _t) sin θ _i. Звідси θ _t монотонно збільшується з θ _i і тому існує деякі θ _i такі, що

\[θ_{i}+θ_{t}=90^o. \nonumber \]

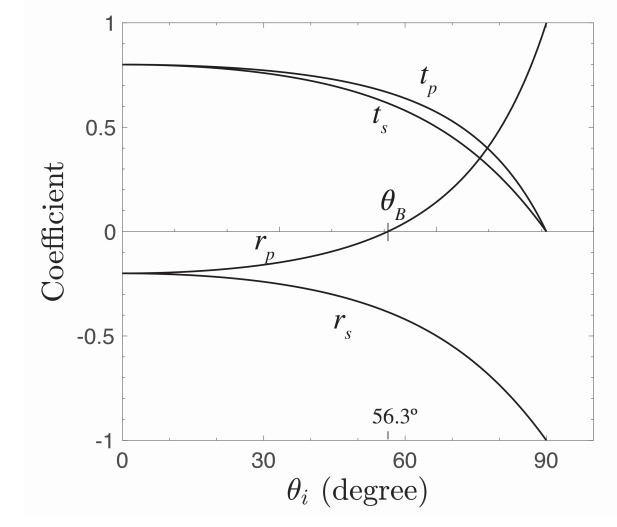
Для цього конкретного кута падіння знаменник (\(\PageIndex{52}\)) нескінченний і, отже, r _p = 0, тобто p-поляризована хвиля взагалі не відбивається. Цей кут падіння називається кутом Брюстера θ _B. З (\(\PageIndex{50}\)) легко побачити, що відображення ніколи не дорівнює нулю для s-поляризації.

Якщо неполяризоване світло падає під кутом Брюстера, відбите світло буде чисто s-поляризованим.

Оскільки під кутом Брюстера s-поляризоване світло відбивається лише частково, а решта передається, пропущене світло під кутом Брюстера є сумішшю s- та p-поляризації. Ми маємо θ _t = 90 ^o − θ _i, звідси sin θ _t = cos θ _i і за законом Снелла (запис θ _i = θ _B):

\[tan(θ_{B})=\dfrac{n_{t}}{n_{i}}. \nonumber \]

Ми бачимо, що завжди є рішення, незалежно від того, чи падає хвиля з матеріалу з найменшим або найбільшим показником заломлення. Для інтерфейсу повітря-скло ми маємо θ _B = 56,3 ^o і θ _t = 33,7 ^o. За (\(\PageIndex{50}\)):

\[r_{s}(θ_{B}=56.3^o)=-0.38 \nonumber \]

так що (0,38) ^{2 /2} = 0,07, або 7% неполяризованого світла відбивається як чисто s-поляризоване світло на межі розділу повітряного скла. Для хвилі, що падає зі скла, θ _B = 33,7 ^о.

На\(\PageIndex{3}\) малюнку показані коефіцієнти відбиття та пропускання s- та p-поляризованих хвиль як функція кута падіння для випадку падіння з повітря на скло. Критичного кута повного відбиття в даному випадку немає. Вказується кут Брюстера. Видно, що коефіцієнти відбиття зменшуються від значень −0,2 для θ _i = 0 ^o до -1 для θ _i = 90 ^o. Коефіцієнти передачі монотонно зменшуються до 0 при θ _i = 90 ^o.

\(\PageIndex{3}\)На малюнку показані коефіцієнти Френеля при падінні хвилі зі скла на повітря. Критичний кут дорівнює θ _{i, crit} = 41.8 ^o, як виведено раніше. При куті повного внутрішнього відбиття абсолютні значення коефіцієнтів відбиття ідентичні 1. Знову існує кут, де відбиття p-поляризованого світла дорівнює нулю θ _B = 33.7 ^o.

Залежно від показників заломлення і кута падіння коефіцієнти відбиття можуть бути негативними. Відбите електричне поле потім має додатковий зсув фази π порівняно з падаючою хвилею. На відміну від цього (за умови, що матеріали без втрат), передається поле завжди знаходиться в фазі з полем падаючого, тобто коефіцієнти передачі завжди позитивні.

1.9.5 Загальне внутрішнє відображення та зникаючі хвилі

Повертаємося до випадку хвилі, що падає зі скла на повітря, тобто n _i = 1,5 і n _t = 1. _{Як було пояснено, тоді існує критичний кут, заданий sinθ i, crit = n т/n i.}

Це еквівалентно

\[k_{x}^t=k_{0}n_{i}sinθ_{i,crit}=k_{0}n_{t} \nonumber \]

Хвильовий вектор k ^t = k _x ^t x + k _z ^t z в z > 0 задовольняє:

\[(k_{x}^t)^2+(k_{z}^t)^2=k_{0}^2n_{t}^2. \nonumber \]

Через (\(\PageIndex{60}\)) ми маємо під критичним кутом

\[k_{z}^t=0. \nonumber \]

Для кутів падіння над критичним кутом маємо: k _x ^t > k ₀ n _t і випливає з (\(\PageIndex{61}\)) що (k _z ^t) ² = k ₀ ² n _t ² − (k _x ^{t 2}) < 0, отже k _z ^t є уявним:

\[k_{z}^t=±(k_{0}^2n_{t}^2-(k_{x}^t)^2)^{1/2}=±i((k_{x}^t)^2-k_{0}^2)^{1/2}, \nonumber \]

де останній квадратний корінь - додатне дійсне число. Можна показати, що вище критичного кута коефіцієнти відбиття є комплексними числами з модулем 1: |r _s | = |r _p | = 1. Це означає, що відбита інтенсивність ідентична інтенсивності падаючого, при цьому коефіцієнти пропускання не дорівнюють нулю! Наприклад, для s-поляризації ми маємо відповідно до (\(\PageIndex{46}\)), (\(\PageIndex{47}\)):

\[t_{s}=1+r_{s}≠0, \nonumber \]

тому що r _s ≠ −1 (хоча |r _s | = 1). Тому є електричне поле в z > 0, задане

\[E(x,z)e^{-iωt}=t_{s}e^{ik_{x}^tx+ik_{z}^tz-iωt}\hat{y}=t_{s}e^{i(k_{x}^tx-ωt)}e^{-z((k_{x}^t)^2-k_{0}^2n_{t}^2)^{1/2}}\hat{y},z>0, \nonumber \]

де ми вибрали знак + в (\(\PageIndex{63}\)), щоб запобігти вибуху поля для z → ∞. Оскільки k _x ^t є реальним, хвиля поширюється в напрямку x. У z-напрямку, однак, хвиля не поширюється. Його амплітуда зменшується експоненціально як функція відстані z до інтерфейсу і тому хвиля обмежується тонким шаром, прилеглим до інтерфейсу. Така завивка називається випливає хвилею. Можна обчислити вектор Пойнтінга хвилі, що ухиляється і виявити, що цей вектор паралельний інтерфейсу. Значить, потік енергії зникаючої хвилі поширюється паралельно інтерфейсу, а саме в напрямку, в якому k ^t _x є позитивним.

Отже, ніяка енергія не транспортується від розділу розділу в повітряну область. Ми повернемося до хвиль, що зникають, в розділі, присвяченому теорії дифракції.

Зовнішні джерела в рекомендованому порядку

1. Відео Youtube - 8.03 - Лект 18 - Індекс заломлення, відображення, рівняння Френеля, Кут Брюстера - Лекція Уолтера Левіна

2. MIT OCW - Відбиття на кордоні повітряного скла: демонстрація відображення поляризованого світла та кута Брюстера.