2.14: Вправа

Last updated
Save as PDF

Page ID: 79077

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Вправа\(\PageIndex{1}\)

Об'єкт розміщується на 90 см зліва від тонкої лінзи в повітрі. Зображення реальне і знаходиться на 99 см праворуч від об'єктива.

Однак якщо середовищем праворуч від лінзи є вода (показник заломлення 1,33), зображення віртуальне і знаходиться на 76 см зліва від лінзи.

І якщо середовище зліва від об'єктива - вода (а праворуч - повітря), зображення реальне і 47 см праворуч від об'єктива.

Обчисліть два радіуси кривизни і показник заломлення скла.

Вправа\(\PageIndex{2}\)

Об'єкт розміщується на 100 см зліва від першої поверхні (А) товстої лінзи (товщина = 10 см) в повітрі. Зображення реальне і знаходиться на 25 см праворуч від другої поверхні (B).

Однак якщо середовищем праворуч від другої поверхні (B) є вода (показник заломлення 1.33), зображення реальне і 41 см праворуч від поверхні B.

І якщо середовище зліва від поверхні А - вода (а праворуч від B - повітря), зображення реальне і 92 см праворуч від об'єктива.

Обчисліть два радіуси кривизни і показник заломлення скла.

Жодна з цих двох проблем, швидше за все, з'явиться в практичній ситуації - але вони є дуже хорошою практикою для складних проблем з лінзами! Рішення на наступній сторінці - але не заглядати, поки ви не спробували їх!

Рішення

1. Перший:

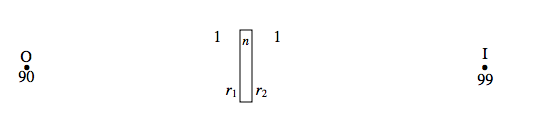
\[\frac{1}{99} = -{1}{90} +\frac{n-1}{r_1}+\frac{1-n}{r_2}.\label{eq:2.14.1} \]

Друге:

\[-\frac{-1.33}{76}=-\frac{1}{90}+\frac{n-1}{r_1}+\frac{1.33-n}{r_2}. \label{eq:2.14.2} \]

(Можливо, у вас виникне спокуса подумати, що ліва сторона цього рівняння повинна бути\(\frac{1}{76}\). Переконайтеся, що ви розумієте, чому це неправильно.)

Третє:

\[\frac{1}{47} = -\frac{1.33}{90}+\frac{n-1.33}{r_1}+\frac{1-n}{r_2}.\label{eq:2.14.3} \]

На цьому фізика закінчена. Все, що потрібно зробити, це вирішити три рівняння для трьох невідомих. Я б почав з того, що дозволив\( x=r_1, y=r_2, z = n\). Рівняння тоді стають:

\[z(x-y)-x+y=0.021212121,\label{eq:2.14.4} \]

\[z(x − y) − x + 1.33 y = − 0.006388889 \label{eq:2.14.5} \]

\[z(x − y) − 1.33 x + y = 0.036054374.\label{eq:2.14.6} \]

Їх легко вирішити:

\(x= − 0.044977, \quad y = − 0.083639, \quad z = + 1.54864.\)

Таким чином

\(r_1 = 22.23 \text{cm},\qquad r_2 = 11.96 \text{cm},\qquad n=1.5549 \text{cm} \)

Лінза - це позитивна лінза меніска (тобто товстіша посередині), обидві поверхні опуклі праворуч. Виглядає це так:

Перший:

\[C_1 = -\frac{1}{100}\label{eq:2.14.7} \]

\[C_2 = -\frac{1}{100} + \frac{n-1}{r_1} = \frac{100n-100-r_1}{100r_1}\label{eq:2.14.8} \]

\[C_3 = \frac{nC_2}{n-10C_2} = \frac{100n^2 - 100n-r_1n}{100r_1n+10r_1 - 1000n + 1000}\label{eq:2.14.9} \]

\[ C_4 = \frac{100n^2-100n - r_1n}{100r_1n+10r_1-1000n+1000}+\frac{1-n}{r_2}=\frac{1}{25}\label{eq:2.14.10} \]

Друге:

\[C_1 = -\frac{1}{100}\label{eq:2.14.11} \]

\[C_2 = -\frac{1}{100}+\frac{n-1}{r_1} = \frac{100n-100-r_1}{100r_1}\label{eq:2.14.12} \]

\[C_3 = \frac{nC_2}{n-10C_2}=\frac{100n^2-100n-r_1n}{100r_1n+10r_1-1000n+1000}\label{eq:2.14.13} \]

\[C_4= \frac{100n^2-100n-r_1n}{100r_1n+10r_1-1000n+1000}+\frac{1.33-n}{r_2} =\frac{1.33}{41}\label{eq:2.14.14} \]

Поки що ми отримали два складних на вигляд рівняння (\(\ref{eq:2.14.10}\)і\(\ref{eq:2.14.14\)) в трьох невідомих\(r_1, r_2\) і\(n\), і ми тільки збираємося приступити до отримання третього рівняння з третього експерименту, після чого нам доведеться зіткнутися з неприємним завданням вирішення трьох рівнянь. Але дивіться! — перш ніж натиснути на, ми можемо виявити, що ми вже можемо вирішити для\(r_2\) з Рівняння\(\ref{eq:2.14.10}\) і\(\ref{eq:2.14.14}\). Я роблю це

\[r_2 = - 43.645 161 29 \text{cm}\label{eq:2.14.15} \]

так що друга поверхня увігнута вліво — тобто вона випирає вправо. Це був несподіваний шматочок удачі! Тепер ми можемо перейти до третього експерименту.

Третє:

\[C_1 = -\frac{1.33}{100}\label{eq:2.14.16} \]

\[C_2 = -\frac{1.33}{100 }+\frac{n-1.33}{r_1}=\frac{100n-133-1.33r_1}{100r_1}\label{eq:2.14.17} \]

\[C_3 = \frac{nC_2}{n-10C_2}=\frac{100n^2-133n-1.33r_1n}{100r_1n+13.3r_1-1000n+1330}\label{eq:2.14.18} \]

\[C_4= \frac{100n^2-133n-1.33r_1n}{100r_1n+13.3r_1 -1000n + 1300}+\frac{1-n}{r_2} = \frac{1}{92}\label{eq:2.14.19} \]

Тепер ми можемо вирішити Рівняння\(\ref{eq:2.14.10}\) і\(\ref{eq:2.14.19}\), або\(\ref{eq:2.14.14}\) і\(\ref{eq:2.14.19}\) для\(r_1\) і\(n\). Дуже сумлінний захоче вирішити їх, використовуючи\(\ref{eq:2.14.10}\), а потім повторити рішення, використовуючи\(\ref{eq:2.14.14}\) і\(\ref{eq:2.14.19}\), і перевірити, що вони дають ту саму відповідь, а потім додатково перевірять, що правильні рішення були отримані шляхом підміни в кожному з трьох рівнянь в\(\ref{eq:2.14.19}\) поворот. Будучи трохи менш сумлінним, я збираюся використовувати рівняння\(\ref{eq:2.14.10}\) і\(\ref{eq:2.14.19}\), а потім перевірити, що отримані рішення задовольняють рівняння\(\ref{eq:2.14.14}\).

Мені легше вирішувати рівняння в\(x\) і,\(y\) а не в\(r_1\) і\(n\), тому я збираюся дозволити\(x = r_1\) і\(y = n\). Потім, маючи на увазі, що ми вже з'ясували\( r_2 = -43.645 161 29\), що, рівняння\(\ref{eq:2.14.10}\) і\(\ref{eq:2.14.19}\) стали, відповідно, після невеликої алгебри і арифметики,

\[\frac{100y^2 -100y -xy}{100xy+10x-1000y+1000} = by +c \label{eq:2.14.20} \]

\[\frac{100y^2-100ay-axy}{100xy+10ax-1000y+1000a}=by+d,\label{eq:2.14.21} \]

де

а = +1,33

б = -0.02291204730

в = +0.06291204630

д =+0,03379161252

Після трохи більш нудної, але рутинної алгебри та арифметики, вони стають

\[Axy^2 +By^2 + C_1xy + D_1x+E_1y+ F_1 = 0\label{eq:2.14.22} \]

\[Axy^2 + By^2+C_2xy+D_2x+E^2y+F_2 = 0, \label{eq:2.14.23} \]

де

А = 2,291204730

Б = 77,08795270

С ₁ = -7,062084 257

Д ₁ = -0,6291204730

Е ₁ = -14,17590540

Ф ₁ = -62,91204730

С ₂ = -4,403431023

Д ₂ = -0,449295447

Е ₂ = -68,74536457

Ф ₂ = -44,92954465.

Тоді ми повинні вирішити ці два рівняння! Їх можна вирішити, наприклад, методом, описаним у розділі 1.9 глави 1 заміток про небесну механіку. Так як у мене вже є комп'ютерна програма, яка робить це, я використовував її і отримав\(x = 15.386908\) і\(y = .1 518865\). Таким чином, розчин для лінз є

\( r_1 = + 15.39 \text{cm} \qquad r_2 = -43.65 \text{cm} \qquad n = 1.519\)

Перша поверхня опукла зліва, а друга - опукла справа. Тобто лінза «жирна», випирає посередині.

Як перевірити, що з нашою арифметикою все в порядку, ми можемо перевірити, що це рішення також задовольняє рівнянню\( \ref{eq:2.14.14}\). (Це робить!)

Як подальша перевірка, читач тепер може захотіти почати з цих чисел і відстані об'єкта 100 см, і подивитися, чи призводить це до трьох відстаней зображення, заданих у вихідній задачі. (Це робить!)

Ще один спосіб вирішення рівнянь\( \ref{eq:2.14.22}\) і\( \ref{eq:2.14.23}\) полягає в відніманні першого з останнього для отримання

\[axy+bx+cy +d =0, \label{eq:2.14.24} \]

коли

\(a\)= 2,658653234

\(b\)= 0,179825026

\(c\)= -54,56945917

\(d\)= 17,98260265.

Потім ви можете висловити\(x\) і функцію\(y\) і замінити в Рівняння\( \ref{eq:2.14.22}\) (або в\( \ref{eq:2.14.23}\), або обидва як чек). Потім у вас є одне кубічне рівняння\(y\), а не два одночасні рівняння в\(x\) і\(y\), як показано нижче:

\[(Ba-Ac_y^3+(E_1a+Bb-C_1c-Ad)y^2+(F_1a+E_1b-D_1c-C_1d)y+F_1b-D_1c =0.\label{eq:2.14.25} \]

Чисельно це

\[329.9799377y^3- 450.4024164y^2 - 77.14660950y - 6.294\times10^{-5} =0. \label{eq:2.14.26} \]

Єдиним позитивним реальним коренем цього є\(y (= n) = 1.518864\), який такий же, як ми отримували раніше. Значення потім\(x (= r_1)\) легко знайти, з Рівняння\(\ref{eq:2.14.24}\), щоб бути 15,3869 см, як і раніше.

Вправа\(\PageIndex{3}\)

Об'єктив, що сходиться має фокусну відстань в повітрі 40 см. Яка його фокусна відстань при зануренні у воду, показника заломлення 1.333?

Через мить роздумів ви вимагатимете, щоб вам сказали показник заломлення скла. Після подальших роздумів ви зробите висновок, що не тільки потрібно знати показник заломлення скла, але і потрібно знати форму (радіуси кривизни поверхонь) лінзи.

Отже, ось питання правильно поставлений.

Двоопукла лінза виготовлена зі скла з показником заломлення 1,5. Радіуси кривизни його поверхонь складають 25 см і 100 см. Яка його фокусна відстань в повітрі? Якою була б його фокусна відстань, якщо зануритися у воду з показником заломлення 4/3? Якою була б його фокусна відстань, якщо занурений у бісульфід вуглецю з показником заломлення 5/3?

Вправа\(\PageIndex{4}\)

Об'єктив має фокусну відстань в повітрі 30 см.

Блок скла з тим же показником заломлення, що і вищевказана лінза, має всередині нього повітряний міхур точно такого ж розміру і форми вищевказаної лінзи. Яка фокусна відстань цього міхура у формі лінзи?

Ви можете запитати себе, чи потрібно знати форму лінзи або показник заломлення скла. Я дозволю тобі замислитися.

Вправа\(\PageIndex{5}\)

Тонкий цементований дуплет виготовляється з двох тонких лінз, зцементованих між собою, як показано на малюнку нижче. Радіуси кривизни в см вказані на кресленні. Показник заломлення лінзи лівої руки є\(n_1\), а лінзи правої руки є\(n_2\). Комбінація призводить до загальної розбіжності дублетних лінз фокусною відстанню 127 см.

В результаті виробничої помилки два типи скла ненавмисно обмінюються, і робиться дублетна лінза, як показано нижче:

Ця комбінація призводить до загальної сходяться дублетної лінзи фокусної лінзи 72 см. Обчисліть показники заломлення двох видів скла.

Ось мої рішення проблем від 3 до 5

Рішення

3. Фокусна відстань в повітрі задається

\(\frac{}{} = 0 +\frac{1.5-1.0}{25} + \frac{1.0-1.5}{-100}, \qquad \text{whence} \underline{\underline{f = 40 \text{cm}}} \)

Фокусна відстань у воді задається

\( \frac{\frac{4}{3}}{f} = 0 + \frac{\frac{3}{2}-\frac{4}{3}}{25} + \frac{\frac{4}{3}-\frac{3}{2}}{-100}, \qquad \text{whence} \underline{\underline{f = 160 \text{cm}}}\)

Фокусна відстань в CS ₂ задається

\(\frac{\frac{5}{3}}{f} = 0 + \frac{\frac{3}{2}-\frac{5}{3}}{25}+\frac{\frac{5}{3}-\frac{3}{2}}{-100}, \qquad \text{whence} \underline{\underline{f = -200 \text{cm}}} \)

4. Незалежно від форми лінзи фокусна відстань скляної лінзи в повітрі задається

\( \frac{1}{f_{\text{lens}}}= (n-1) \left(\frac{1}{r_1}-\frac{1}{r_2}\right),\)

тоді як фокусна відстань міхура у склі задається

\(\frac{1}{f_{\text{bubble}}}= (n-1) \left(\frac{1}{r_1}-\frac{1}{r_2}\right).\)

Таким чином

\(\underline{\underline{f_\text{bubble} = -n \times f_\text{lens} = -30n \quad \text{cm}}}\)

5. Фокусні відстані двох дублетів пов'язані з показниками заломлення

\( -\frac{1}{127}= \frac{n_1-1}{40} +\frac{n_2-n_2}{-22}+\frac{1-n_2}{50}\)

\(\frac{1}{72} = \frac{n_2-1}{40}+\frac{n_1-n_2}{-22}+\frac{1-n_1}{50}\)

Ці рівняння можна переписати

\( 1968n_1-18288n_2 + 803 = 0 \)

\(1296n_1 -1395n_2 + 374 = 0,\)

з розчинами

\(\underline{\underline{ n_1 = 1.521 \qquad n_2= 1.682}}\)