Skip to main content
LibreTexts - Ukrayinska

2.12: Основні літаки

  1. Last updated
  2. Save as PDF
  • Page ID
    79069

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розглянемо товсту лінзу, або систему з двох розділених лінз. На малюнку II.21,\(F_1\) є першою фокусною точкою і\(H_1\) є першою основною площиною. У Digure II.22\(F_2\) є другою фокусною точкою і\(H_2\) є другою основною площиною

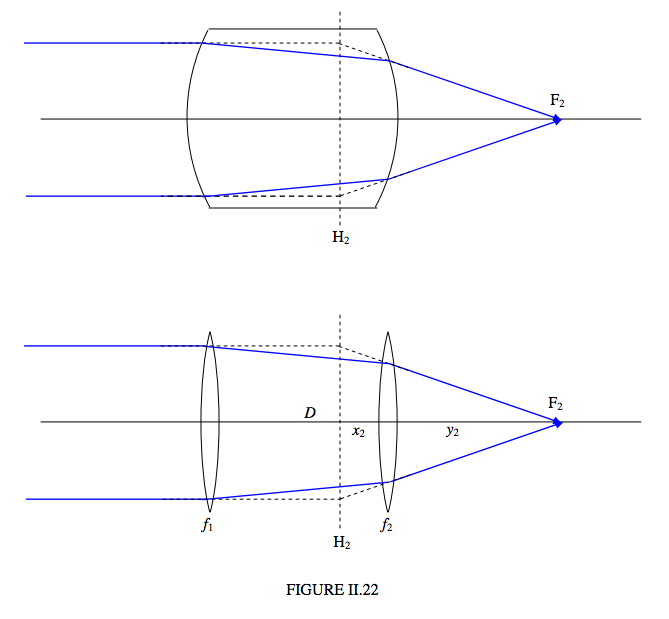
    Тепер я посилаюся на другу частину малюнка II.22, і я вважаю, що фокусні відстані двох об'єктивів є\(f_1\) і\(f_2\), і відстань між ними є\(D\). Я зараз пропоную читачеві розрахувати відстані\(x_2\) і\(y_2\). Відстань\(x_2\) можна обчислити, враховуючи деякі подібні трикутники (які читачеві доведеться додати до креслення), а відстань\(y_2\) можна обчислити шляхом обчислення збіжностей\(C_1, C_2,C_3,C_4\) у звичному для цього часу способом. Ви повинні отримати

    \[ x_2 = \frac{Df_2}{f_1+f_2-D}. \label{eq:2.12.1} \]

    і

    \[ y_2=\frac{f_2(f_1-D)}{f_1+f_2-D}. \label{eq:2.12.2} \]

    Я також запрошую читача уявити, що дві лінзи повинні бути замінені одним об'єктивом, розташованим у площині,\(H_2\) щоб довести світло до того\(F_2\) ж фокусу, який був отриманий двома оригінальними лінзами. Питання: якою має бути фокусна відстань f цього єдиного об'єктива? Відповідь\(x_2 + y_2\), очевидно, що приходить до

    \[ f = \frac{f_1f_2}{f_1+f_2-D}. \label{eq:2.12.3} \]

    Окуляр оптичного приладу, такого як телескоп або мікроскоп, як правило, являє собою комбінацію двох (або більше) лінз, які називаються польовою лінзою та лінзою ока. Вони, як правило, розташовані так, що відстань між ними дорівнює половині суми фокусних відстаней двох лінз. Тепер ми побачимо, що ця композиція з двома лінзами, виготовленими з одного скла, відносно вільна від хроматичної аберації.

    Нагадаємо собі, що потужність об'єктива в повітрі дається за рахунок

    \[ P = \frac{1}{f}=(n-1)\left(\frac{1}{r_1}+\frac{1}{r_2}\right) \label{eq:2.12.4} \]

    Тут\(r_1\) і\(r_2\) знаходяться радіуси кривизни двох поверхонь, і\(n\) знаходиться показник заломлення скла. Коротше кажучи, я збираюся написати рівняння\(\ref{eq:2.12.4}\) як

    \[ P = \frac{1}{f} = \mu S, \label{eq:2.12.5} \]

    де\(\mu = n-1\) і\(S= \left(\frac{1}{r_1}+\frac{1}{r_2}\right) \). Таким чином, рівняння\(\ref{eq:2.12.3}\) можна записати

    \[ P = \mu(S_1+S_2)- \mu ^2SD_1S_2 \label{eq:2.12.6} \]

    Це рівняння показує, як положення фокуса\(F_2\) змінюється залежно від кольору. Зокрема,

    \[ \frac{dP}{d\mu} = S_1 + S_2 - 2 \mu DS_1S_2, \label{eq:2.12.7} \]

    який показує, що положення\(F_2\) не змінюється залежно від кольору за умови, що відстань між лінзами

    \[ D= \frac{S_1+S_2}{2\mu S_1S_2}. \label{eq:2.12.8} \]

    Повертаючись до Рівняння\(\ref{eq:2.12.5}\), ми бачимо, що це перекладається на

    \[ \underline{\underline{D= \frac{1}{2}(f_1+f_2).}} \label{eq:2.12.9} \]