2.10: Проектування ахроматичного дублета

Last updated
Save as PDF

Page ID: 79081

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Це не намір цієї глави вивчати аберації лінз. Однак конструкція ахроматичної дублетної лінзи піддається такому розрахунку, який ми робимо в цьому розділі.

Комбінація двох лінз в контакті, що сходиться лінзи з коронного скла та слабшої розходяться лінзи з крем'яного скла, може бути сконструйована так, що комбінація являє собою сходяться лінзу, яка майже ахроматична. Кремінне скло трохи щільніше коронного скла, і має більш високий показник заломлення і більшу дисперсійну силу.

Дисперсійна\(\omega\) сила скла зазвичай визначається як

\[\omega= \frac{n^{(F)}-n^{(C)}}{n^{(D)}-1}.\label{eq:2.10.1} \]

Тут C, D і F відносяться до довжин хвиль C, D і F ліній Фраунгофера в сонячному спектрі, які відповідно H\(\alpha\) (656,3 нм), Na I (589,3 нм), H\(\beta\) (486,1 нм), і які можуть вільно називатися «червоним», «жовтим» і «синім». Типове значення для коронного скла становило б близько 0,016, а типове значення для крем'яного скла становило б близько 0,028.

Ахроматичний дуплет, як правило, виготовляється з позитивної коронної скляної лінзи, потужність якої є позитивною, але яка зменшується зі збільшенням довжини хвилі (тобто до червоної), цементованої до більш слабкої лінзи з крем'яним склом, потужність якої негативна, а також зменшується (за величиною) зі збільшенням довжини хвилі. Сума двох ступенів є позитивною, і мало змінюється з довжиною хвилі, переживаючи невеликий мінімум. Як правило, при конструюванні ахроматичного дублета буде дотримуватися дві вимоги: 1. Потужність або фокусна відстань жовтим кольором буде вказано, і 2. Ви хотіли б, щоб потужність червоного кольору була такою ж, як сила синього кольору, і мало відрізнялася між ними.

Розглянемо дублет, проілюстрований на малюнку II.15, побудований з двоопуклої коронкової лінзи та двоувігнутої крем'яної лінзи.

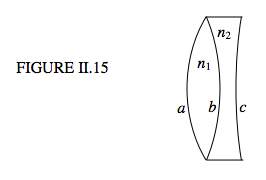
Я вказав показники і радіуси кривизни. Потужність (зворотна фокусній відстані) першої лінзи сама по собі становить

\[ P_1 = (n_1-1) \left(\frac{1}{a}+\frac{1}{b}\right),\label{eq:2.10.2} \]

і потужність другого об'єктива

\[ P_2 = -(n_2-1)\left( \frac{1}{b}+\frac{1}{c}\right). \label{eq:2.10.3} \]

Я напишу їх коротко, в очевидних позначеннях, як

\[ P_1 = k_1(n_1-1), \qquad P_2 = -k_2(n_2-1). \label{eq:2.10.4a,b} \]

Але нам потрібні такі рівняння для кожної з трьох довжин хвиль, таким чином:

\[ P_1^{(C)} = k_1(n_1^{(C)}-1), \qquad P_2^{(C)} = -k_2(n_2^{(C)}-1), \label{eq:2.10.5a,b} \]

\[ P_1^{(D)} = k_1(n_1^{(D)}-1), \qquad P_2^{(D)} = -k_2(n_2^{(D)}-1),\label{eq:2.10.6a,b} \]

\[P_1^{(F)} = k_1(n_1^{(F)}-1), \qquad P_2^{(F)} = -k_2(n_2^{(F)}-1). \label{eq:2.10.7a,b} \]

Тепер ми хочемо задовольнити дві умови. Одна з них полягає в тому, що загальна потужність повинна бути вказана:

\[P_1^{(D)} +P_2^{(D)} = P^{(D)} . \label{eq:2.10.8} \]

Інша полягає в тому, що загальна потужність в червоному дорівнює загальній потужності в синьому кольорі, і тепер я використовую рівняння\(\ref{eq:2.10.5a,b}\) і\(\ref{eq:2.10.7a,b}\):

\[ k_1(n^{(C)}_1- 1) - k_2(n^{(C)}_2-1)= k_1(n^{(F)}_1- 1) - k_2(n^{(F)}_2-1).\label{eq:2.10.9} \]

На перестановці це стає

\[ k_1(n^{(F)}_1- n^{(C)}_1) = k_2(n^{(F)}_2-n^{(C)}_2). \label{eq:2.10.10} \]

Тепер, використовуючи рівняння\(\ref{eq:2.10.1}\) і\(\ref{eq:2.10.6a,b}\), ми отримуємо умову, що сили будуть однаковими в червоному та синьому кольорах:

\[ \omega_1P_1 + \omega_2 P_2 = 0. \label{eq:2.10.11} \]

Наприклад, припустимо, що ми хочемо, щоб фокусна відстань жовтого кольору становила 16\(P^{(D)}= 0.0625\) см (см ^-1) і що дисперсійні сили складають 0,016 і 0,028. Рівняння,\(\ref{eq:2.10.8}\) а\(\ref{eq:2.10.11}\) потім скажіть нам, що ми повинні мати\( P_1^{(D)}= 0.14583\) см ^-1\) і\(P_2^{(D)}= -0.083\) см ^-1. (\(f_1 =6.86\)см і\(f_2 = -12.0\) см).

Якщо ми хочемо зробити першу лінзу рівноопуклою, так що\(a = b\), і якщо\(n_1 = 1.5\), Рівняння\(\ref{eq:2.10.2}\) говорить нам, що\(a\) = 6,86 см. Якщо\(n_2 = 1.6\), Рівняння\(\ref{eq:2.10.3}\) потім говорить нам, що\(c = −144\) см. \(c\)Це негативно говорить нам, що наше припущення, що кремінь лінза була увігнута праворуч, було неправильним; воно опукле праворуч.

Вправа\(\PageIndex{1}\)

Припустимо, що замість того, щоб зробити коронну лінзу рівноопуклою, ви вирішили зробити останню поверхню плоскою — тобто\(c\) = ∞. Що ж тоді повинно\(a\) і\(b\) бути?

Відповіді. \(a\) = 6.55 cm, \(b\) = 7.20 cm.