2.9: Виведення збільшення
- Page ID
- 79072
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
На малюнку II.14 показаний оптичний елемент, що розділяє середовища індексів\(n_1\) і\(n_2\). Я намалював елемент як інтерфейс, хоча він однаково міг би бути об'єктивом (або, якби я складав малюнок, дзеркало). Зображення висоти\(h'\) формується на відстані\(q\) предмета висоти\(h\) на відстані\(p\).
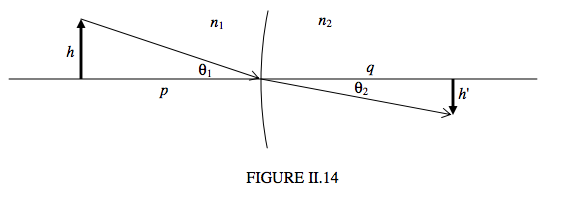
Припускаючи, як ніколи, що кути невеликі, ми маємо
\[\text{magnification} = \dfrac{\theta_2q}{\theta_1p}.\]
Але закон Снелла, для малих кутів, є\(n_1\theta_1 = n_2\theta_2\), і тому
\[ \text{magnification} = \dfrac{n_1q}{n_2p} = \frac{C_1}{C_2}. \label{eq:2.9.1} \]
