12.3: Модель Еренфест

12.3.1 Опис моделі

Гра з перегортанням монет - це «дводержавна» ланцюжок Маркова. Для застосувань фізики нас часто цікавлять ланцюги Маркова, де кількість можливих станів величезна (наприклад, термодинамічні мікростани). Модель Ehrenfest - приємний і простий приклад, який ілюструє багато властивостей таких ланцюгів Маркова. Ця модель була введена командою чоловіка-фізика Павла і Тетяни Еренфест в 1907 році, з метою вивчення фізики дифузії.

Припустимо, у нас є дві коробки, позначені A і B, і загальна кількість$N$ помітних частинок для розподілу між двома коробками. У даний момент часу нехай будуть$n$ частинки в коробці А, а отже,$N-n$ частинки в коробці B. Тепер ми неодноразово застосовуємо наступну процедуру:

1. Випадковим чином вибираємо одну з$N$ частинок (з однаковою ймовірністю).
2. З імовірністю$q$ перемістіть обрану частинку з якого б ящика вона не опинилася, в іншу коробку. В іншому випадку (з ймовірністю$1-q$) залиште частинку в її поточній коробці.

Малюнок$\PageIndex{1}$: Схема моделі Ehrenfest.

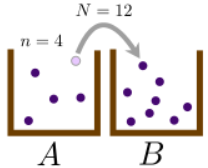
Якщо є$n$ частинки в коробці А, то ми маємо$n/N$ ймовірність вибору частинки в полі А, а потім ймовірність перемістити цю частинку в поле B. Дотримуючись аналогічної логіки для всіх інших можливостей, ми досягаємо трьох можливих результатів:$q$

• Переміщення частинки від А до Б: ймовірність$nq/N$
• Переміщення частинки від B до A: ймовірність$(N-n)q/N$
• Залиште систему без змін: ймовірність$1-q$

Ви можете перевірити, що (i) ймовірності підсумовуються до$1$, і (ii) це резюме відповідає дійсності для кінцевих випадків$n=N$ і$n=0$.

12.3.2 Маркова ланцюг Опис

Ми можемо позначити стани системи, використовуючи ціле число$n \in \{0, 1, \dots, N\}$, відповідне кількості частинок у полі А.$N+1$ Можливі стани, а діаграма стану виглядає наступним чином:

Малюнок$\PageIndex{2}$: Діаграма стану моделі Ehrenfest.

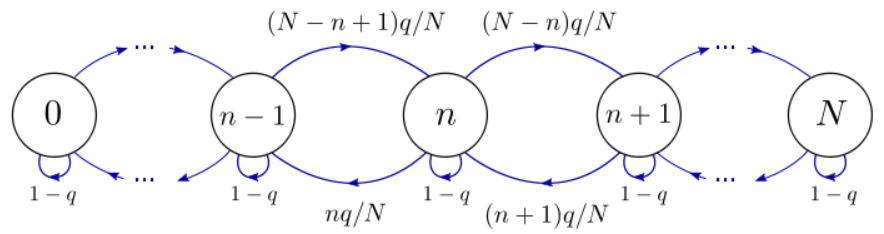
Припустимо, ми починаємо в стані$n_{0}=N$, помістивши всі частинки в поле А. Як ми неодноразово застосовуємо процедуру Еренфеста, система проходить послідовність станів$\{n_0 = N, n_1, n_2, n_3, \dots\}$, яку можна охарактеризувати як ланцюг Маркова. Побудувавши стан$n_{k}$ проти числа кроку$k$, ми бачимо випадкову траєкторію, подібну до наведеної нижче:

Малюнок$\PageIndex{3}$: Зразок траєкторії моделі Еренфеста з$N=50$ і$q=0.5$.

Зверніть увагу, що система швидко відходить від свого початкового стану$n=50$, і осідає в поведінку, де вона коливається навколо середнього стану$n=25$. Шукатимемо стаціонарний розподіл, при якому ймовірність знаходження в кожному стані незмінна на наступних кроках. Дозвольте$\pi_{n}$ позначити стаціонарну ймовірність перебування в стані$n$. Згідно з правилом Байєса, цей розподіл ймовірностей повинен задовольнити

$$\begin{align} \pi_n &= P(n|n-1) \pi_{n-1} + P(n|n) \pi_n + P(n|n+1) \pi_{n+1} \\ & = \frac{N-n+1}{N} \,q\, \pi_{n-1} + (1-q) \pi_n + \frac{n+1}{N}\,q\, \pi_{n+1}. \end{align}$$

Ми можемо розібратися,$\pi_{n}$ використовуючи два різних методи. Перший метод полягає у використанні наших знань статистичної механіки. У стаціонарному розподілі кожна окрема частинка повинна мати однакові шанси опинитися в коробці А або коробці Б. Існують$2^{N}$ можливі коробкові призначення, кожне з яких енергетично еквівалентно і, отже, мають рівні ймовірності. Звідси ймовірність знаходження$n$ частинок в коробці А - це кількість способів збирання$n$ частинок$N \choose n$, яке ділиться на кількість можливих боксових завдань. Це дає

$$\pi_n = {N\choose n} \, 2^{-N}.$$

Підставивши в правило Байєса формулу, ми можемо переконатися, що цей розподіл дійсно є стаціонарним. Зверніть увагу, що$\pi_{n}$ виявляється незалежним від$q$ (ймовірність перенесення обраної частинки в іншу коробку). Інтуїтивно$q$ керує тим, як «швидко» ми переносимо частинки з однієї коробки в іншу. Тому він повинен впливати на те, наскільки швидко система досягає свого стаціонарного або «рівноважного» поведінки, але не самого стаціонарного розподілу.

12.3.3 Детальний баланс

Є ще один спосіб з'ясувати$\pi_{n}$, який не покладатися на вгадування відповіді одним пострілом. Припустимо, ми вибираємо пару сусідніх станів$n+1$,$n$ і, і припустимо, що швидкість, з якою відбувається$n \rightarrow n+1$ перехід, така ж, як і швидкість$n \rightarrow n+1$, з якою відбувається протилежний перехід. Така умова гарантовано не тримається, але якщо воно тримається для кожної пари станів, то розподіл ймовірностей обов'язково стаціонарний. Така ситуація називається детальним балансом. З точки зору ймовірностей стану та ймовірностей переходу, детальний баланс вимагає

$$P(n+1|n) \, \pi_n = P(n|n+1) \, \pi_{n+1} \qquad \forall n \in \{0,\dots,N\},$$

для цього Маркова ланцюг. Підключивши ймовірності переходу, отримаємо рекурсійне відношення

$$\pi_{n+1} = \frac{N-n}{n+1}\, \pi_{n}.$$

Те, що зручно в цьому рекурсійному відношенні, полягає в тому, що воно включає лише$\pi_{n}$ і$\pi_{n+1}$, на відміну від відношення правил Байєса, яке також включало$\pi_{n-1}$. За допомогою індукції ми можемо тепер легко показати, що

$$\pi_n = {N\choose n} \pi_0.$$

Зберігаючи ймовірність$\sum_n \pi_n = 1$, ми можемо це показати$\pi_0 = 2^{-N}$. Це призводить до

$$\pi_n = {N\choose n} 2^{-N},$$

що є результатом, про який ми раніше здогадалися, використовуючи чисто статистичні аргументи.

Для більш складних ланцюгів Маркова, можливо, неможливо вгадати стаціонарний розподіл; в таких випадках детальний аргумент балансу часто є найкращим підходом. Однак зауважте, що детальна умова балансу не гарантовано відбудеться. Є деякі ланцюги Маркова, які не підкоряються детальному балансу, тому нам завжди потрібно перевіряти, чи результат деталізованої умови балансу є самоузгодженим (тобто, що він дійсно може підкорятися кожній парі станів).