Skip to main content
LibreTexts - Ukrayinska

5.1: Основний алгоритм

  1. Last updated
  2. Save as PDF
  • Page ID
    79628

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Найкращий спосіб зрозуміти, як працює гаусова елімінація, - це працювати на конкретному прикладі. Розглянемо наступну\(N=3\) проблему:

    \[\begin{bmatrix}1 &2 &3 \\ 3 &2 &2 \\ 2 &6 &2\end{bmatrix} \begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix}3 \\ 4 \\ 4\end{bmatrix}.\]

    Алгоритм гаусової елімінації складається з двох різних фаз: зменшення рядків та зворотної заміщення.

    5.1.1 Зменшення R рядків

    У фазі скорочення рядків алгоритму ми маніпулюємо матричним рівнянням так, щоб матриця стала верхньою трикутною (тобто всі записи нижче діагоналі дорівнюють нулю). Щоб цього домогтися, зауважимо, що один ряд ми можемо відняти з іншого ряду, не змінюючи розчин. Насправді, ми можемо відняти будь-яке кратне рядка.

    Усунемо (обнулити) елементи нижче діагоналі в певному порядку: зверху вниз по кожному стовпчику, потім зліва направо для послідовних стовпчиків. Для нашого\(3\times 3\) прикладу елементи, які ми маємо намір усунути, і порядок, в якому ми їх усунемо, позначаються кольоровими цифрами\(0\)\(1\), а на\(2\) наступному малюнку:

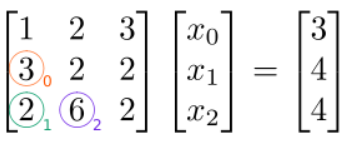
    clipboard_ee51b6655ea8f5114a5fdf27ae6c5a4fd.png
    Малюнок\(\PageIndex{1}\)

    Перший елемент матриці, який ми хочемо усунути, знаходиться в\((1,0)\) (помаранчеве коло). Щоб її усунути, віднімаємо, з цього ряду, кратний ряду\(0\). Ми будемо використовувати коефіцієнт\(3/1=3\):

    \[(3x_0 + 2x_1 + 2x_2) - (3/1)(1x_0 + 2x_1 + 3x_2) = 4 - (3/1) 3\]

    Використовуваний нами\(3\) коефіцієнт визначається наступним чином: ми ділимо елемент матриці на\((1,0)\) (який ми маємо намір усунути) на елемент at\((0,0)\) (який є тим, що по діагоналі в тому ж стовпці). В результаті\(x_{0}\) зникає термін пропорційний, і ми отримуємо наступні модифіковані лінійні рівняння, що володіють тим же розв'язком:

    clipboard_ea9ac17b2d6a51a7ab06a9dfded14addf.png
    Малюнок\(\PageIndex{2}\)

    (Зауважте, що ми змінили запис у векторі з правого боку, а не тільки матрицю на лівій стороні!) Далі усуваємо елемент при\((2,0)\) (зелене коло). Для цього віднімаємо, з цього ряду, кратний ряду\(0\). Коефіцієнт, який слід використовувати\(2/1=2\), який є елементом при\((2,0)\) діленні на\((0,0)\) (діагональний) елемент:

    \[(2x_0 + 6x_1 + 2x_2) - (2/1)(1x_0 + 2x_1 + 3x_2) = 4 - (2/1) 3\]

    Результатом є

    clipboard_e2f868d69e640f2417ce294c0831f5479.png
    Малюнок\(\PageIndex{3}\)

    Далі усуваємо\((2,1)\) елемент (синій коло). Цей елемент лежить у стовпці\(1\), тому ми усуваємо його, віднімаючи кратну рядку\(1\). Коефіцієнтом використання є\(2/(-4)=-0.5\), який є\((2,1)\) елементом, розділеним на\((1,1)\) (діагональний) елемент:

    \[(0x_0 + 2x_1 - 4x_2) - (2/(-4))(0x_0 - 4x_1 - 7x_2) = -5 - (2/(-4)) (-2)\]

    Результатом є

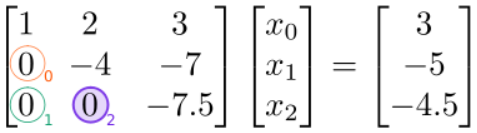
    clipboard_e2b08908b35369e1242c4b67cc2443259.png
    Малюнок\(\PageIndex{4}\)

    Ми завершили фазу скорочення рядків, так як матриця з лівого боку верхньо-трикутна (тобто всі записи нижче діагоналі встановлені на нуль).

    5.1.2 Зворотна заміна

    У фазі зворотного заміщення зчитуємо розчин від самого нижнього ряду до самого верхнього ряду. Спочатку оглядаємо нижній ряд:

    clipboard_e88050c7d67e5377372205efdc8d491ca.png
    Малюнок\(\PageIndex{5}\)

    Завдяки скороченню рядків всі елементи матриці в цьому рядку дорівнюють нулю, крім останнього. Отже, ми можемо прочитати рішення

    \[x_{2}=(-4.5)/(-7.5)=0.6.\]

    Далі дивимося на ряд вище:

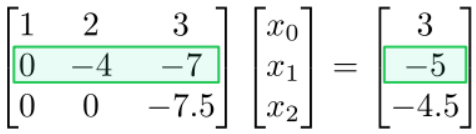
    clipboard_e1a889d08902264079ef840ac8e9c2cfd.png
    Малюнок\(\PageIndex{6}\)

    Це рівняння за участю\(x_{1}\) і\(x_{2}\). Але з попереднього кроку зворотної підміни ми знаємо\(x_{2}\). Отже, ми можемо вирішити

    \[x_1 = [-5 - (-7) (0.6)] / (-4) = 0.2.\]

    Нарешті, дивимося на рядок вище:

    clipboard_e88e368fb3f4b56d5b06e6434386c14d4.png
    Малюнок\(\PageIndex{7}\)

    Це включає в себе всі три змінні\(x_{0}\)\(x_{1}\), і\(x_{2}\). Але ми вже знаємо\(x_{1}\) і\(x_{2}\), тому можемо прочитати рішення для\(x_{0}\). Кінцевий результат

    \[\begin{bmatrix}x_0 \\ x_1 \\ x_2\end{bmatrix} = \begin{bmatrix}0.8 \\ 0.2 \\ 0.6\end{bmatrix}.\]

    5.1.3 Виконання

    Давайте підсумуємо складові алгоритму гаусової елімінації, і проаналізуємо, скільки кроків проходить кожна частина:

    Зменшення рядків
    • Крок вперед через ряди. Для кожного ряду\(n\) \(N\)сходинок
    • Виконуємо поворот (мова піде нижче). \(N-n +1 \sim N\)сходинок
    • Крок вперед через ряди більше ніж\(n\). Для кожного такого ряду\(m\) \(N-n \sim N\)сходинок
    • Відніміть\((A'_{mn}/A'_{nn})\) час рядка\(n\) з рядка\(m\) (\(\mathbf{A}'\)де поточна матриця). Це виключає елемент матриці при\((m,n)\). \(O(N)\)арифметичні операції
    Задня заміна
    • Крок назад через ряди. Для кожного ряду\(n\) \(N\)сходинок
    • Підставляємо в розчини\(x_{m}\) для\(m>n\) (які вже знайдені). Значить, знайти\(x_{n}\). \(N-n \sim O(N)\)арифметичні операції

    (Процедура «повороту» ще не обговорювалася; ми зробимо це в наступному розділі.)

    Зроблено висновок, що час виконання фази скорочення рядків\(O(N^{3})\) масштабується як, а час виконання фази зворотного заміщення масштабується як\(O(N^{2})\). Отже, загальний час виконання алгоритму масштабується як\(O(N^{3})\).