12.E: Електромагнетизм (вправи)

1. Спостерігається частинка із зарядом 1,0 С і масою 1,0 кг, що рухається повз точку Р зі швидкістю\((1.0\ \text{m}/\text{s})\hat{\mathbf{x}}\). Електричне поле в точці Р є\((1.0\ \text{V}/\text{m})\hat{\mathbf{y}}\), а магнітне поле -\((2.0\ \text{T})\hat{\mathbf{y}}\). Знайдіть силу, яку відчуває частинка. (Перевірка відповіді доступна на сайті lightandmatter.com)

2. Для позитивно зарядженої частинки, що рухається через магнітне поле\(\mathbf{v}\)\(\mathbf{B}\), напрямки\(\mathbf{F}\) векторів, і векторів пов'язані правилом:

\[\begin{align*} \mathbf{v} & \text{along the fingers, with the hand flat}\\ \mathbf{B} & \text{along the fingers, with the knuckles bent}\\ \mathbf{F} & \text{along the thumb} \end{align*}\]

Створіть тривимірну модель трьох векторів за допомогою олівців або згорнутих аркушів паперу, щоб представити вектори, зібрані з хвостами разом. Зробіть всі три вектора перпендикулярними один одному. Тепер запишіть всілякі способи, за допомогою яких правило може бути переписано шляхом скремблювання трьох символів\(\mathbf{v}\)\(\mathbf{B}\), і\(\mathbf{F}\). Посилаючись на вашу модель, які є правильними, а які неправильними?

3. Заряджена частинка звільняється від спокою. Ми бачимо, що він починає рухатися, і коли він йде, ми помічаємо, що його шлях починає кривим. Чи можемо ми сказати, чи має ця область простору\(\mathbf{E}\neq 0\), або\(\mathbf{B}\neq 0\), або обидва? Припустимо, що крім можливих електричних і магнітних сил немає ніяких інших сил, і що поля, якщо вони присутні, рівномірні.

4. Заряджена частинка знаходиться в області простору, в якій є однорідне магнітне поле\(\mathbf{B}=B\hat{\mathbf{z}}\). Електричного поля немає, і ніякі інші сили не діють на частинку. У кожному конкретному випадку опишіть майбутній рух частинки, враховуючи її початкову швидкість.

1. \(\mathbf{v}_\text{o}=0\)
2. \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{z}}\)
3. \(\mathbf{v}_\text{o}=(1\ \text{m}/\text{s})\hat{\mathbf{y}}\)

5. (а) Лінійний заряд із зарядом на одиницю довжини\(\lambda\) рухається зі швидкістю\(v\) вздовж власної довжини. Скільки заряду проходить даний момент часу\(dt\)? Що таке результуючий струм? \ hwans {hwans: linechargecurrent}
(b) Показати, що одиниці вашої відповіді частково працюють правильно.

Це являє собою фізичну модель електричного струму, і це була б фізично реалістична модель пучка частинок, що рухаються у вакуумі, наприклад, електронний промінь у телевізійній трубці. Це не фізично реалістична модель руху електронів в струмоведучому дроті або іонів у вашій нервовій системі; рух носіїв заряду в цих системах набагато складніше і хаотичніше, і є заряди обох знаків, так що загальний заряд дорівнює нулю. Але навіть коли модель фізично нереальна, вона все одно дає правильні відповіді, коли ви використовуєте її для обчислення магнітних ефектів. Це примітний факт, який ми не будемо доводити. Зацікавлений читач посилається на Е.М. Перселл, Електрика і магнетизм, McGraw Hill, 1963.

6. Два паралельних дроти довжини\(L\) несуть струми\(I_1\) і\(I_2\). Вони розділені відстанню\(R\), і ми припускаємо\(R\) набагато менше\(L\), ніж, щоб наші результати для довгих, прямих проводів були точними. Метою цієї задачі є обчислення магнітних сил, що діють між проводами.
(а) Жоден дріт не може зробити силу на себе. Тому наш перший крок у обчисленні сили проводу 1 на дроті 2 полягає в тому, щоб знайти магнітне поле, зроблене тільки проводом 1, в просторі, зайнятому проводом 2. Висловіть це поле в терміні заданих величин. (Перевірка відповіді доступна на lightandmatter.com)
(b) Давайте змоделюємо струм в дроті 2, роблячи вигляд, що всередині нього є лінійний заряд, що володіє щільністю на одиницю довжини\(\lambda_2\) і рухається зі швидкістю\(v_2\). \(v_2\)Віднесіть\(\lambda_2\) і до струму\(I_2\), використовуючи результат завдання 5 а. тепер знайдемо магнітну силу провід 1 виробляє на дроті 2, в перерахунку на\(I_1\)\(I_2\),,\(L\), і\(R\). \ hwans {hwans: forcebetween twoodwires}
(c) Показати, що одиниці відповіді на частину b працюють як ньютони.

7. Припустимо, заряджена частинка рухається через область простору, в якій є електричне поле, перпендикулярне її вектору швидкості, а також магнітне поле, перпендикулярне як вектору швидкості частинки, так і електричному полю. Покажіть, що буде одна конкретна швидкість, з якою частка може рухатися, що призводить до загальної сили нуля на ній. Пов'язати цю швидкість з величинами електричного і магнітного полів. (Таке розташування, зване фільтром швидкості, є одним із способів визначення швидкості невідомої частинки.)

8. Наступні дані дають результати двох експериментів, в яких заряджені частинки вивільнялися з однієї і тієї ж точки в просторі, і сили на них вимірювалися:

q 1 = 1 μ С	\(\mathbf{v}_1=(1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_1=(-1 mN)\mathbf{\hat y}\)
q 2 = - 2 μ С	\(\mathbf{v}_2=(-1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_2=(-2 mN)\mathbf{\hat y}\)

Дані недостатньо для визначення вектора магнітного поля; продемонструйте це шляхом надання двох різних векторів магнітного поля, обидва з яких узгоджуються з даними.

9. Наступні дані дають результати двох експериментів, в яких заряджені частинки вивільнялися з однієї і тієї ж точки в просторі, і сили на них вимірювалися:

q 1 = 1 нК	\(\mathbf{v}_1=(1 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_1=(5 mN)\mathbf{\hat x}+(2 mN)\mathbf{\hat y}\)
q 2 = 1 нК	\(\mathbf{v}_2=(3 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_2=(10 mN)\mathbf{\hat x}+(4 mN)\mathbf{\hat y}\)

Чи існує в цій точці ненульове електричне поле? Ненульове магнітне поле?

10. Ця проблема є продовженням проблеми 6. Зверніть увагу, що відповідь на задачу 6 b наведено на сторінці 930.

1. Поміняючи 1-е і 2-е у відповіді на задачу 6 б, яка величина магнітної сили від дроту 2, що діє на провід 1? Чи відповідає це третьому закону Ньютона?
2. Припустимо, струми знаходяться в одному напрямку. Зробіть ескіз і скористайтеся правилом правої руки, щоб визначити, чи провід 1 тягне дріт 2 до нього, або відштовхує його.
3. Застосуйте правило праворуч знову, щоб знайти напрямок сили дроту 2 на дроті 1. Чи погоджується це з третім законом Ньютона?
4. Що станеться, якби струм проводу 1 був у зворотному напрямку порівняно з проводом 2?

11. (а) На фото вакуум-трубчастого апарату на малюнку о на стор. 656 виведіть напрямок магнітного поля від руху електронного пучка. (Відповідь дається у відповіді на самоперевірку на цій сторінці.)
(б) Виходячи з вашої відповіді на частину а, знайдіть напрямок струмів в котушках.
(c) В якому напрямку йдуть електрони в котушках?
(г) Чи струми в котушках відштовхують струми, що складаються з пучка всередині трубки, або притягують їх? Перевірте свою відповідь, порівнявши з результатом завдання 10.

12. Заряджена частинка маси\(m\) і заряду\(q\) рухається по колу за рахунок однорідного магнітного поля величини\(B\), яке вказує перпендикулярно площині кола.

1. Припустимо, частка позитивно заряджена. Зробіть ескіз, що показує напрямок руху і напрямок поля, і покажіть, що результуюча сила знаходиться в правильному напрямку, щоб виробляти круговий рух.
2. Знайти радіус кола\(r\), з точки зору,\(m\),,\(q\)\(v\), і\(B\). (Перевірка відповіді доступна на сайті lightandmatter.com)
3. Покажіть, що ваш результат з частини b має правильні одиниці.
4. Обговоріть всі чотири змінні, що виникають у правій частині вашої відповіді з частини b Чи мають вони сенс? Наприклад, що має статися з радіусом, коли магнітне поле стає сильнішим? Чи поводиться ваше рівняння таким чином?
5. Повторюйте свій результат, щоб він дав кутову частоту частинки\(\omega\), з точки зору інших змінних, і показати, що\(v\) випадає. (Перевірка відповіді доступна на сайті lightandmatter.com)

Заряджена частинка може бути прискорена в круговому пристрої, який називається циклотроном, в якому магнітне поле - це те, що утримує їх від прямого виходу. Тому ця частота відома як частота циклотронів. Частинки прискорюються іншими силами (електричними силами), які є змінним струмом. Поки електричне поле працює на правильній частоті циклотрону для типу маніпульованих частинок, воно буде синхронізуватися з частинками, даючи їм поштовх у правильному напрямку кожного разу, коли вони проходять повз. Частинки прискорюються, тому це працює лише тому, що частота циклотрона не залежить від швидкості.

a/ Задача 13.

13. Кожна фігура представляє рух позитивно зарядженої частинки. Точки дають позиції частинок через рівні проміжки часу. У кожному випадку визначте, чи був рух викликаний електричною силою, магнітною силою або силою тертя, і поясніть свої міркування. По можливості визначте напрямок магнітного або електричного поля. Всі поля однорідні. У (а) частка зупиняється на мить у верхньому правому куті, але потім повертається вниз і вліво, втягуючи ті самі точки. У (b) він зупиняється у верхньому правому куті і залишається там.

14. Одна модель атома водню має електрон, що кружляє навколо протона зі швидкістю\(2.2\times10^6\) м/с, на орбіті радіусом 0,05 нм. (Хоча електрон і протон дійсно обертаються навколо свого загального центру мас, центр маси дуже близький до протона, оскільки він в 2000 разів масивніший. Для цієї проблеми припустимо, що протон нерухомий.)

1. Розглядайте кружляє електрон як струмовий контур, і обчисліть струм.
2. Оцініть магнітне поле, створене в центрі атома електроном. (Перевірка відповіді доступна на сайті lightandmatter.com)
3. Чи відчуває протон ненульову силу від магнітного поля електрона? Поясніть.
4. Чи відчуває електрон магнітне поле від протона? Поясніть.
5. Чи відчуває електрон магнітне поле, створене власним струмом? Поясніть.
6. Чи існує електрична сила, що діє між протоном і електроном? Якщо так, розрахуйте його. (Перевірка відповіді доступна на сайті lightandmatter.com)
7. Чи існує гравітаційна сила, що діє між протоном і електроном? Якщо так, розрахуйте його.
8. Внутрішня сила потрібна, щоб утримати електрон на своїй орбіті - інакше він підкоряється першому закону Ньютона і йшов би прямо, залишаючи атом. Виходячи з ваших відповідей на попередні частини, яка сила або сили (електричні, магнітні та гравітаційні) значно сприяють цій внутрішній силі? (На основі проблеми Арнольда Аронса.)

15. Рівняння\(B_z=\beta kIA/c^2r^3\) знайдено на сторінці 666 для віддаленого поля диполя. Покажіть, як там стверджується, що константа\(\beta\) повинна бути безмежною.

16. Наступні дані дають результати трьох експериментів, в яких заряджені частинки вивільнялися з однієї і тієї ж точки в просторі, і сили на них вимірювалися:

q 1 = 1 С	\(\mathbf{v}_1=0\)	\(\mathbf{F}_1=(1 N)\mathbf{\hat y}\)
q 2 = 1 С	\(\mathbf{v}_2=(1 m/s)\mathbf{\hat x}\)	\(\mathbf{F}_2=(1 N)\mathbf{\hat y}\)
q 3 = 1 С	\(\mathbf{v}_3=(1 m/s)\mathbf{\hat z}\)	\(\mathbf{F}_3=0\)

Визначте електричне і магнітне поля. (Перевірка відповіді доступна на сайті lightandmatter.com)

17. Якщо поставити в чотири рази більше струму через соленоїд, у скільки разів більше енергії зберігається в його магнітному полі? (Перевірка відповіді доступна на сайті lightandmatter.com)

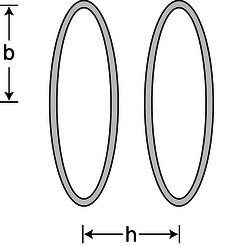
b/Задача 18.

18. Котушка Гельмгольца визначається як пара однакових кругових котушок, що лежать в паралельних площинях і розділених відстанню\(h\), рівним їх радіусу\(b\). (Кожна котушка може мати більше одного витка дроту.) Струм циркулює в одному напрямку в кожній котушці, тому поля мають тенденцію підсилювати один одного у внутрішній області. Ця конфігурація має перевагу в тому, що вона досить відкрита, так що інші апарати можуть бути легко розміщені всередині і піддані полю, залишаючись видимими зовні. Вибір\(h=b\) результатів у максимально рівномірному полі поблизу центру. Фотографія котушки Гельмгольца була показана на малюнку o на сторінці 656.
(а) Знайдіть відсоток падіння поля в центрі однієї котушки, порівняно з повною силою в центрі всього апарату. (Перевірка відповідей доступна на lightandmatter.com)
(b) Яке значення\(h\) (не дорівнює, щоб\(b)\) ця різниця у відсотках дорівнювала нулю? (Перевірка відповіді доступна на сайті lightandmatter.com)

c/Задача 19.

19. На малюнку зображена вкладена пара кругових дротяних петель, що використовуються для створення магнітних полів. (Скручування відводів - це практичний трюк для зменшення магнітних полів, які вони сприяють, тому поля дуже майже те, що ми очікували б для ідеального кругового циклу струму.) Система координат нижче, щоб полегшити обговорення напрямків у просторі. Одна петля знаходиться в\(y-z\) площині, інша - в\(x-y\) площині. Кожна з петель має радіус 1,0 см, і несе 1,0 А в напрямку, зазначеному стрілкою.

1. Обчисліть магнітне поле, яке було б вироблено однією такою петлею, в її центрі. (Перевірка відповіді доступна на сайті lightandmatter.com)
2. Опишіть напрямок магнітного поля, яке було б вироблено в його центрі петлею в одній лише\(x-y\) площині.
3. Те ж саме виконайте для іншої петлі.
4. Обчисліть величину магнітного поля, виробленого двома петлями в поєднанні, в їх загальному центрі. Опишіть її напрямок. (Перевірка відповіді доступна на сайті lightandmatter.com)

d/Задача 20.

20. Чотири довгих дроти розташовані, як показано, так, щоб їх перетин утворював квадрат, з з'єднаннями на кінцях так, щоб струм протікав через всі чотири перед виходом. Зверніть увагу, що струм знаходиться праворуч в двох задніх проводах, а зліва в передніх проводах. Якщо розміри квадрата поперечного перерізу (висота і спереду назад) є\(b\), знайдіть магнітне поле (величину і напрямок) уздовж довгої центральної осі. (Перевірка відповіді доступна на сайті lightandmatter.com)

21. У задачі 16 три експерименти дали достатньо інформації для визначення обох полів. Чи можна сконструювати процедуру так, щоб, використовуючи всього два таких експерименту, ми завжди могли знайти\(\mathbf{E}\) і\(\mathbf{B}\)? Якщо так, спроектуйте його. Якщо ні, то чому б і ні?

22. Використовуйте закон Біот-Саварта, щоб вивести магнітне поле довгого прямого дроту, і показати, що це відтворює результат прикладу 6 на сторінці 658.

23. (а) Змініть розрахунок на сторінці 663, щоб визначити складову магнітного поля аркуша заряду, який перпендикулярний аркушу. (Перевірка відповіді доступна на lightandmatter.com)
(б) Показати, що ваша відповідь має правильні одиниці.
(c) Показати, що ваша відповідь наближається до нуля, коли\(z\) наближається до нескінчен
(d) Що відбувається з вашою відповіддю у випадку\(a=b\)? Поясніть, чому це має сенс.

24. Розглянемо два соленоїда, один з яких менше, щоб його можна було поставити всередину іншого. Припустімо, що вони досить довгі, щоб кожен з них лише значно сприяв полю всередині себе, а внутрішні поля майже однорідні. Розглянемо конфігурацію, де малий знаходиться всередині великого з їх струмами, що циркулюють в одному напрямку, і другу конфігурацію, в якій струми циркулюють в протилежних напрямках. Порівняйте енергії цих конфігурацій з енергією, коли соленоїди знаходяться далеко один від одного. Виходячи з цього міркування, яка конфігурація стабільна, і в якій конфігурації маленький соленоїд, як правило, скручується або виплюне? \ hwint {hwhint: вкладені соленоїди}

e/Задача 25.

25. (а) Соленоїд можна уявити як ряд кругових контурів струму, які розташовані вздовж їх загальної осі. Інтегруйте результат прикладу 12 на сторінці 671, щоб показати, що поле на осі соленоїда можна записати як\(B=(2\pi k\eta/c^2)(\cos\beta+\cos\gamma)\), де\(\gamma\) кути\(\beta\) і визначені на малюнку.
(b) Показати, що в межі, де соленоїд дуже довгий, цей точний результат узгоджується з приблизним, отриманим у прикладі 13 на сторінці 674, використовуючи закон Ампера.
(c) Зауважте, що, на відміну від розрахунку з використанням закону Ампера, цей діє в точках, які знаходяться поблизу гирла соленоїда, або навіть поза ним повністю. Якщо соленоїд довгий, в якій точці на осі знаходиться поле, рівне половині його значення в центрі соленоїда?
(d) Що відбувається з вашим результатом, коли ви застосовуєте його до точок, які знаходяться дуже далеко від соленоїда? Чи має це сенс?

26. Першим кроком у доведенні закону Ампера на сторінці 675 є показати, що закон Ампера дотримується у випадку, показаному на малюнку f /1, де кругова петля Ампера зосереджена на довгому прямому дроті, перпендикулярному площині петлі. Проведіть цей розрахунок, використовуючи отриманий результат для поля дроту, яке було встановлено без використання закону Ампера.

27. Певна область простору має магнітне поле, задане\(\mathbf{B}=bx\hat{\mathbf{y}}\). Знайти електричний струм, що протікає через квадрат\(z=0\),\(0\le x \le a\) заданий, і\(0\le y \le a\). (Перевірка відповіді доступна на сайті lightandmatter.com)

f/Оболонка наутілуса є приблизно логарифмічною спіраллю, типу в задачі 28.

28. Виконайте обчислення аналогічно тому, що в задачі 54, але для логарифмічної спіралі,\(r=we^{u\theta}\) визначеної, і показати, що поле є\(B=(kI/c^2u)(1/a-1/b)\). Зверніть увагу, що рішення задачі 54 наведено в задній частині книги.

29. (а) Для геометрії, описаної в прикладі 8 на стор. 661, знайдіть поле в точці, яка лежить в площині проводів, але не між проводами, на відстані\(b\) від центральної лінії. Використовуйте ту ж техніку, що і в цьому прикладі.
(b) Тепер повторіть розрахунок, використовуючи техніку, продемонстровану на сторінці 666. Інтеграли майже однакові, але тепер міркування зворотні: ви вже знаєте\(\beta=1\), і хочете знайти невідоме поле. Єдина відмінність в інтегралах полягає в тому, що ви облицьовуєте різну область площини, щоб змоделювати струми в двох проводах. Зауважте, що ви не можете розділити область, яка містить цікаву точку, оскільки техніка використовує поле віддаленого диполя. (Перевірка відповіді доступна на сайті lightandmatter.com)

30. (а) Довгий, худий соленоїд складається з\(N\) витків дроту, обмотаного рівномірно навколо порожнистого циліндра довжини\(\ell\) і площі поперечного перерізу\(A\). Знайдіть його індуктивність. (Перевірка відповіді доступна на lightandmatter.com)
(b) Показати, що ваша відповідь має правильні одиниці, щоб бути індуктивністю.

31. Розглянемо два соленоїда, один з яких менше, щоб його можна було поставити всередину іншого. Припустимо, що вони досить довгі, щоб діяти як ідеальні соленоїди, так що кожен з них лише значно сприяє полю всередині себе, а внутрішні поля майже рівномірні. Розглянемо конфігурацію, де маленький частково знаходиться всередині і частково висить з великого, при цьому їх струми циркулюють в одному напрямку. Їх осі обмежені збігом.
(а) Знайдіть різницю в магнітній енергії між конфігурацією, де соленоїди розділені, і конфігурацією, де малий вставляється у велику. Ваше рівняння буде включати довжину\(x\) частини малого соленоїда, який знаходиться всередині великого, а також інші відповідні змінні, що описують два соленоїди. (Перевірка відповіді доступна на lightandmatter.com)
(b) На основі вашої відповіді на частину а знайдіть силу, що діє між соленоїдами. (Перевірка відповіді доступна на сайті lightandmatter.com)

g/Задача 32.

32. Перевірте закон Ампера у випадку, показаному на малюнку, припускаючи відоме рівняння для поля дроту. Провід, що несе струм,\(I\) проходить перпендикулярно через центр прямокутної амперської поверхні. Довжина прямокутника нескінченна, тому обчислювати внески кінців необов'язково.

33. Мета цієї проблеми полягає в тому, щоб знайти, як коефіцієнт посилення трансформатора залежить від його конструкції.
(а) Кількість петель дроту\(N\), в соленоїді змінюється, зберігаючи постійну довжину. Від чого залежить імпеданс\(N\)? Скажіть свою відповідь як пропорційність, наприклад,\(Z\propto N^3\) або\(Z\propto N^{-5}\).
(b) Для заданої напруги змінного струму, що подається на індуктор, як залежить магнітне поле\(N\)? Потрібно враховувати як залежність поля соленоїда від\(N\) для заданого струму, так і вашу відповідь на частину а, яка впливає на струм.
(в) Тепер розглянемо трансформатор, що складається з двох соленоїдів. Вхідна сторона має\(N_1\) петлі, а на виході\(N_2\). Бажаємо дізнатися, як\(V_2\) залежить вихідна напруга від\(N_1\)\(N_2\), і вхідної напруги\(V_1\). Текст вже встановився\(V_2\propto V_1N_2\), тому залишається тільки знайти залежність від\(N_1\). Використовуйте свій результат з частини b, щоб досягти цього. Коефіцієнт\(V_2/V_1\) називається коефіцієнтом посилення напруги.

34. Завдання 33 стосувалося залежності коефіцієнта посилення трансформатора від кількості петель проводу у вхідному соленоїді. Проведіть аналогічний аналіз того, як коефіцієнт посилення залежить від частоти, на якій працює схема.

h/Задача 35.

35. П-подібний провід здійснює електричний контакт з другим, прямим проводом, який котиться по ньому вправо, як показано на малюнку. Вся справа занурена в однорідне магнітне поле, яке перпендикулярно площині ланцюга. Опір прокатного дроту набагато більше, ніж у У.
(а) Знайти напрямок сили на дроті на основі збереження енергії.
(b) Перевірте напрямок сили за допомогою правильних правил.
(в) Знайти величину сили, що діє на дріт. Існує не один спосіб зробити це, але, будь ласка, зробіть це, використовуючи закон Фарадея (який працює, хоча змінюється сама амперська поверхня, а не поле). (Перевірка відповіді доступна на lightandmatter.com)
(d) Розглянемо, як змінилася б відповідь на частину а, якби напрямок поля було змінено, а також зробіть випадок, коли напрямок руху прокатного дроту змінюється. Переконайтеся, що це узгоджується з вашою відповіддю на частину c.

36. Заряджена частинка знаходиться в русі зі швидкістю\(v\), в області вакууму, через яку проходить електромагнітна хвиля. В якому напрямку повинна рухатися частинка, щоб мінімізувати сумарну силу, що діє на неї? Розглянемо обидві можливості для знака заряду. (На основі проблеми Девіда Реймонда.)

i/Задача 37.

37. Дротова петля опору\(R\) і площі\(A\), що лежить в\(y-z\) площині, потрапляє через неоднорідне магнітне поле\(\mathbf{B}=kz\hat{\mathbf{x}}\), де\(k\) знаходиться постійна. \(z\)Вісь вертикальна.
(а) Знайти напрямок сили на дроті на основі збереження енергії.
(b) Перевірте напрямок сили за допомогою правильних правил.
(c) Знайдіть магнітну силу на дроті. (Перевірка відповіді доступна на сайті lightandmatter.com)

38. Конденсатор має паралельні пластини площі\(A\), розділені на відстань\(h\). Якщо між пластинами є розрідження, то закон Гаусса дає\(E=4\pi k\sigma=4\pi kq/A\) поле між пластинами, і поєднуючи це з\(E=V/h\), знаходимо\(C=q/V=(1/4\pi k)A/h\). (а) Узагальнити це похідне до випадку, коли між пластинами є діелектрик. (b) Припустимо, що у нас є список можливих матеріалів, які ми могли б вибрати як діелектрики, і ми хочемо побудувати конденсатор, який матиме максимально можливу щільність енергії\(U_e/v\), де\(v\) об'єм. Для кожного діелектрика ми знаємо його діелектричну проникність\(\epsilon\), а також максимальне електричне поле, яке\(E\) він може витримати, не руйнуючись і дозволяючи іскрам перетинатися між пластинами. Напишіть максимальну щільність енергії з точки зору цих двох змінних і визначте цифру заслуг, яку можна було б використовувати, щоб вирішити, який матеріал буде найкращим вибором.

39. (а) Для кожного члена, що з'являється на правій стороні рівнянь Максвелла, наведіть приклад повсякденної ситуації, яку він описує.
(b) Більшість людей, які роблять розрахунки в системі одиниць СІ, не використовують\(k\) і\(k/c^2\). Замість цього вони висловлюють все з точки зору констант

\[\begin{align*} \epsilon_\text{o}&=\frac{1}{4\pi k} \text{and} \\ \mu_\text{o}&=\frac{4\pi k}{c^2} . \end{align*}\]

Перепишіть рівняння Максвелла з точки зору цих констант, виключаючи\(k\) і\(c\) всюди.

40. (а) Доведіть, що в електромагнітній площині хвиля половина енергії знаходиться в електричному полі і половина в магнітному полі.
(б) Виходячи з вашого результату з частини а, знайдіть постійну пропорційності у співвідношенні\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}dv\), де\(d \mathbf{p}\) імпульс частини площини світлової хвилі, що міститься в обсязі\(dv\). Вектор\(\mathbf{E}\times\mathbf{B}\) відомий як вектор Пойнтінга. (Для виконання цієї проблеми потрібно знати релятивістський зв'язок між енергією та імпульсом променя світла.) (Перевірка відповіді доступна на сайті lightandmatter.com)

41. (а) Промінь світла має площу поперечного перерізу\(A\) і потужність\(P\),\(P\) тобто кількість джоулів в секунду, які входять у вікно, через яке проходить промінь. Знайти щільність енергії\(U/v\) в терміні\(P\)\(A\), і універсальні константи.
(б) Знайти\(\tilde{\mathbf{E}}\) і\(\tilde{\mathbf{B}}\), амплітуди електричного і магнітного полів, в терміні\(P\)\(A\), і універсальні константи (тобто ваша відповідь не повинна включати\(U\) або\(v\)). Вам знадобиться результат завдання 40 а Реальний промінь світла зазвичай складається з багатьох коротких хвиль, а не однієї великої синусоїди, але не турбуйтеся про це. (Перевірка відповіді доступна на lightandmatter.com)\ hwhint {hwhint:solarconstant}
(c) Промінь сонячного світла має інтенсивність\(P/A=1.35\times10^3\ \text{W}/\text{m}^2\), припускаючи відсутність хмар або атмосферного поглинання. Це відоме як сонячна постійна. Обчислюйте\(\tilde{\mathbf{E}}\) і\(\tilde{\mathbf{B}}\) порівняйте з силою статичних полів, які ви відчуваєте\(E \sim 10^6\ \text{V}/\text{m}\) в повсякденному житті: в грозу, і\(B \sim 10^{-3}\) Т для магнітного поля Землі. (Перевірка відповіді доступна на сайті lightandmatter.com)

j/Задача 42.

42. Циркулярний паралельно-пластинчастий конденсатор, показаний на малюнку, заряджається з часом, причому різниця напруг на обкладинках змінюється як\(V=st\), де\(s\) постійна. Пластини мають радіус\(b\), а відстань між ними дорівнює\(d\). Припустимо\(d \ll b\), щоб електричне поле між пластинами було рівномірним, причому паралельно осі. Знайдіть індуковане магнітне поле в точці між пластинами, на відстані\(R\) від осі. \ hwhint {hwhint: кругова кришка} (перевірка відповіді доступна на сайті lightandmatter.com)

43. Позитивно заряджена частинка звільняється з спокою біля початку в\(t=0\), в області вакууму, через яку проходить електромагнітна хвиля. Частинка прискорюється у відповідь на хвилю. У цій області простору хвиля змінюється як\(\mathbf{E}=\hat{\mathbf{x}}\tilde{E}\sin\omega t\)\(\mathbf{B}=\hat{\mathbf{y}}\tilde{B}\sin\omega t\), і ми припускаємо, що частка має відносно велике значення\(m/q\), так що її реакція на хвилю млява, і вона ніколи не закінчується рухається з будь-якою швидкістю, порівнянною зі швидкістю світла. Тому нам не потрібно турбуватися про просторові зміни хвилі; ми можемо просто уявити, що це однорідні поля, накладені якимось зовнішнім механізмом на цю область простору.
(a) Знайти координати частинки як функції часу. (Перевірка відповіді доступна на сайті lightandmatter.com)
(б) Показати, що рух обмежується тим\(-z_{max}\leq z \leq z_{max}\), де\(z_{max} = 1.101\left(q^2\tilde{E}\tilde{B}/m^2\omega^3\right)\).

44. Електромагнітні хвилі повинні мати свої електричні та магнітні поля перпендикулярні один одному. (Протягом усієї цієї проблеми, припустимо, ми говоримо про хвилі, що рухаються через вакуум, і що існує лише одна синусоїда, що рухається в одному напрямку, а не суперпозиція синусоїдальних хвиль, що проходять один через одного.) Припустимо, хтось стверджує, що вони можуть зробити електромагнітну хвилю, в якій електричне і магнітне поля лежать в одній площині. Довести, що це неможливо на основі рівнянь Максвелла.

45. Повторюємо самоперевірку на стор. 710, але з однією зміною процедури: після того як зарядимо конденсатор, розмикаємо ланцюг, а потім продовжуємо спостереження.

46. На сторінці 713 я довів, що\(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\) на кордоні між двома речовинами, якщо немає вільного струму і поля статичні. Насправді кожне з чотирьох рівнянь Максвелла має на увазі обмеження з подібною структурою. Деякі є обмеженнями на компонентах поля, паралельних межі, а інші - обмеження на перпендикулярні частини. Оскільки деякі поля, згадані в рівняннях Максвелла, є електричними та магнітними полями\(\mathbf{E}\)\(\mathbf{B}\), а інші - допоміжними полями\(\mathbf{D}\) і\(\mathbf{H}\), деякі обмеження мають справу з\(\mathbf{E}\) і\(\mathbf{B}\), інші з\(\mathbf{D}\) і\(\mathbf{H}\). Знайдіть інші три обмеження.

47. (а) На малюнку j на сторінці 714 показана порожниста сфера з\(\mu/\mu_\text{o}=x\) внутрішнім радіусом\(a\) та зовнішнім радіусом\(b\), який піддався зовнішньому полю\(\mathbf{B}_\text{o}\). Знаходження полів на екстер'єрі, в оболонці та всередині вимагає знаходження набору полів, що задовольняє п'яти граничним умовам: (1) далеко від сфери поле повинно наближатися до постійної\(\mathbf{B}_\text{o}\); (2) на зовнішній поверхні сфери поле повинно мати\(\mathbf{H}_{\parallel,1}=\mathbf{H}_{\parallel,2}\), як обговорюється на сторінці 713; (3) таке ж обмеження застосовується на внутрішній поверхні сфери; (4) і (5) є додаткове обмеження на поля на внутрішній і зовнішній поверхнях, як знайдено в задачі 46. Мета цієї задачі полягає в тому, щоб знайти рішення для полів, і з нього довести, що внутрішнє поле однорідне, і задане

\[\begin{equation*} \mathbf{B} = \left[\frac{9x}{(2x+1)(x+2)-2\frac{a^3}{b^3}(x-1)^2}\right]\mathbf{B}_\text{o} . \end{equation*}\]

Це дуже складна проблема для вирішення з перших принципів, тому що неочевидно, яку форму повинні мати поля, і якби вам не сказали, ви, напевно, не здогадалися б, що внутрішнє поле буде рівномірним. Однак ми могли б здогадатися, що як тільки сфера стає поляризованою зовнішнім полем, вона стане диполем\(r\gg b\), і в, поле буде рівномірним полем, накладеного на поле диполя. Виходить, що навіть близько до сфери розчин має саме таку форму. Для того, щоб завершити рішення, нам потрібно знайти поле в оболонці (\(a\lt r\lt b\)), але єдиний спосіб, яким це поле може збігатися з детальною кутовою варіацією внутрішніх та зовнішніх полів, було б, якби це було також суперпозиція рівномірного поля з дипольним полем. Кінцевий результат полягає в тому, що ми маємо чотири невідомі: міцність дипольної складової зовнішнього поля, міцність рівномірної та дипольної компонентів поля всередині оболонки та міцність рівномірного внутрішнього поля. Ці чотири невідомі повинні бути визначені шляхом накладення обмежень (2) через (5) вище.
(б) Показати, що вираз з частини а має фізично розумну поведінку в залежності від\(x\) і\(a/b\).

48. Дві довгі паралельні смужки тонкої металевої фольги утворюють конфігурацію, схожу на довгий вузький сендвіч. Повітряний зазор між ними має висоту\(h\), ширина кожної смуги -\(w\), а довжина їх дорівнює\(\ell\). Кожна смуга несе струм\(I\), і ми припускаємо для конкретності, що струми знаходяться в протилежних напрямках, так що магнітна сила\(F\), між смугами відштовхуюча.
(а) Знайти силу в межі\(w\gg h\). (Перевірка відповіді доступна на сайті lightandmatter.com)
(б) Знайдіть силу в межі\(w\ll h\), яка схожа на два звичайних дроти.
(c) Обговоріть взаємозв'язок між двома результатами.

49. Припустимо, нам надається постійний магніт зі складною, асиметричною формою. Опишіть, як серія вимірювань за допомогою магнітного компаса може бути використана для визначення сили та напрямку його магнітного поля в якійсь цікавій точці. Припустимо, що ви можете бачити лише напрямок, в якому осідає стрілка компаса; ви не можете виміряти діючий на неї крутний момент.

50. На сторінці 680\(x\hat{\mathbf{y}}\) був обчислений завиток. Тепер розглянемо поля\(x\hat{\mathbf{x}}\) і\(y\hat{\mathbf{y}}\).
(а) Намалюйте ці поля.
(б) Використовуючи ту ж техніку явно побудови невеликого квадрата, доведіть, що їх локони обидва нульові. Не використовуйте компонентну форму локона; це був один крок у виведенні складової форми локона.

51. Якщо ви дивитеся фільм, який відтворюється назад, деякі вектори змінюють свій напрямок. Наприклад, люди ходять назад, а вектори швидкості перевернуті навколо. Інші вектори, такі як сили, тримають той самий напрямок, наприклад, гравітація все ще тягне вниз. Електричне поле - ще один приклад вектора, який не обертається: позитивні заряди все ще позитивні у всесвіті, що обертаються часом, тому вони все ще утворюють розходяться електричні поля, а також для сходяться полів навколо негативних зарядів.
(а) Як поводиться імпульс матеріального об'єкта під час зміни часу? (Рішення в pdf-версії книги)
(б) Закони фізики все ще діють у зворотному часом Всесвіті. Наприклад, показати, що якщо два матеріальних об'єкта взаємодіють, а імпульс зберігається, то імпульс все ще зберігається у всесвіті, що обертається часом. (рішення у pdf-версії книги)
(c) Обговоріть, як будуть вести себе струми та магнітні поля під час зміни часу. \ hwhint {hwhint:timereversalem}
(d) Аналогічно, показати, що\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) рівняння все ще діє при зміні часу.

52. Ця проблема є більш просунутим дослідженням ідей зміни часу, запроваджених у задачі 51.
(а) У цій проблемі ми припустили, що заряд не перевертає свій знак під час зміни часу. Припустимо, ми робимо протилежне припущення, що заряд дійсно змінює свій знак. Це ідея, представлена Річардом Фейнманом: що антиматерія - це дійсно матерія, яка подорожує назад у часі! Визначте властивості зміни часу\(\mathbf{E}\) і\(\mathbf{B}\) під цим новим припущенням і покажіть,\(d\mathbf{p}\propto\mathbf{E}\times\mathbf{B}\) що все ще діє під час зміни часу.
(б) Показати, що рівняння Максвелла є симетричними по часу, тобто, що якщо поля\(\mathbf{E}(x,y,z,t)\) і\(\mathbf{B}(x,y,z,t)\) задовольняють рівняння Максвелла, то так роблять\(\mathbf{E}(x,y,z,-t)\) і\(\mathbf{B}(x,y,z,-t)\). Продемонструйте це як при можливих припущеннях щодо заряду, так\(q\rightarrow q\) і\(q\rightarrow -q\).

53. Мета цієї задачі полягає в тому, щоб довести, що константа пропорційності\(a\) в рівнянні\(dU_m=aB^2 dv\), для щільності енергії магнітного поля, задана\(a=c^2/8\pi k\) як стверджується на стор. 665. Геометрія, яку ми будемо використовувати, складається з двох аркушів струму, як сендвіч, що не має нічого між ними, але деяким вакуумом, в якому є магнітне поле. Струми знаходяться в протилежних напрямках, і ми можемо уявити їх як з'єднані між собою на кінцях, щоб утворити повний ланцюг, як трубка з паперу, яка була розчавлена майже плоска. Листи мають довжини\(L\) в напрямку, паралельному струму, і ширини\(w\). Їх розділяє відстань\(d\), яке, для зручності, ми припускаємо невелике в порівнянні з\(L\) і\(w\). Таким чином, внесок кожного аркуша в поле є рівномірним і може бути наближений виразом\(2\pi k\eta/c^2\).
(а) Зробіть малюнок, подібний до малюнка 11.2.1 на сторінці 664, і покажіть, що в цій конфігурації протилежного струму магнітні поля двох аркушів посилюються в області між ними, створюючи подвійне поле, але скасовують зовні.
(b) За аналогією з випадком однієї нитки дроту, сила одного аркуша на інший є\(ILB_1\), де\(I=\eta w\) є загальним струмом в одному аркуші, і\(B_1=B/2\) це поле, яке сприяє лише один з аркушів, оскільки лист не може зробити ніякої чистої сили на собі. Грунтуючись на своєму кресленні і правилі правої руки, покажіть, що ця сила відштовхуюча.
Для решти проблеми розглянемо процес, при якому листи починають торкатися, а потім відокремлюються на відстань\(d\). Оскільки сила між листами відштовхує, вони виконують механічну роботу над зовнішнім світом, коли вони відокремлені, майже так само, як поршень в двигуні працює, коли гази всередині циліндра розширюються. У той же час, однак, існує індукована ЕРС, яка прагнула б гасити струм, тому для підтримки постійного струму енергію доведеться зливати з акумулятора. Існує три типи енергії, що беруть участь: збільшення енергії магнітного поля, збільшення енергії зовнішнього світу та зменшення енергії в міру розрядження акумулятора. (Ми припускаємо, що листи мають дуже малий опір, тому не задіяний омічний нагрів.) (Перевірка відповіді доступна на сайті lightandmatter.com)
(c) Знайдіть механічну роботу, виконану листами, що дорівнює збільшенню енергії зовнішнього світу. Покажіть, що ваш результат може бути заявлений з точки зору\(\eta\), кінцевого обсягу\(v=wLd\), і нічого іншого, крім числових і фізичних констант. (Перевірка відповіді доступна на сайті lightandmatter.com)
(г) Живлення, що подається акумулятором\(P=I\Delta V\), є\(P=I\Gamma_E\) (як, але з ЕРС замість різниці напруги), а циркуляція подається\(\Gamma=-d\Phi_B/dt\). Негативний знак говорить про те, що батарея розряджається. Розрахуйте енергію, що подається акумулятором, і, як в частині c, покажіть, що результат може бути заявлений як в плані\(\eta\)\(v\), так і універсальних констант. (Перевірка відповіді доступна на сайті lightandmatter.com)
(e) Знайти збільшення енергії магнітного поля, з точки зору\(\eta\)\(v\), і невідомої константи\(a\). (Перевірка відповіді доступна на lightandmatter.com)
(f) Використовуйте збереження енергії, щоб пов'язати свої відповіді з частин c, d та e, і вирішити для\(a\). (Перевірка відповіді доступна на сайті lightandmatter.com)

k/Задача 54.

54. Магнітні котушки часто загортаються в кілька шарів. На малюнку показаний особливий випадок, коли шари все обмежені єдиною площиною, утворюючи спіраль. Оскільки товщина проводів (плюс їх ізоляція) фіксована, то спіраль, яка виходить, є математичним типом, відомим як спіраль Архімеда, в якій витки рівномірно розташовані. Рівняння спіралі - це\(r=w\theta\), де\(w\) постійна. Для спіралі, яка починається від\(r=a\) і закінчується на\(r=b\), показати, що поле в центрі задається\((kI/c^2w)\ln b/a\). (рішення в pdf-версії книги)

Contributors and Attributions

Template:ContribCrowell