12.1: Детальніше про магнітне поле

11.1.1 Магнітні сили

У цьому розділі я припускаю, що ви знаєте кілька основних уявлень про теорію відносності Ейнштейна, як описано в розділах 7.1 та 7.2. Якщо ваш типовий робочий день не включає ракетні кораблі або прискорювачі частинок, всі ці речі щодо відносності можуть звучати як опис якогось химерного футуристичного світу, який є повністю гіпотетичним. Існує, однак, релятивістський ефект, який виникає в повсякденному житті, і він очевидний і драматичний: магнетизм. Магнетизм, як ми обговорювали раніше, - це взаємодія між рухомим зарядом і іншим рухомим зарядом, на відміну від електричних сил, які діють між будь-якою парою зарядів незалежно від їх руху. Релятивістські ефекти слабкі для швидкостей, які невеликі порівняно зі швидкістю світла, і середня швидкість, з якою електрони дрейфують через дріт, досить низька (сантиметри в секунду, як правило), так як відносність може бути позаду вражаючий ефект, як автомобіль піднімається електромагнітом, що висить з кран? Ключовим є те, що матерія майже ідеально електрично нейтральна, а електричні сили тому скасовуються майже ідеально. Магнітні сили дійсно не дуже сильні, але електричні сили ще слабкіші.

А як щодо слова «відносність» в назві теорії? Здавалося б, проблематично, якщо рухомі заряди взаємодіють інакше, ніж стаціонарні заряди, оскільки рух - це питання думки, залежно від вашої системи відліку. Магнетизм, однак, приходить не для знищення відносності, а для її виконання. Магнітні взаємодії повинні існувати відповідно до теорії відносності. Щоб зрозуміти, як це може бути, розглянемо, як поводяться час і простір в відносності. Спостерігачі в різних рамках відліку розходяться в думках про довжину вимірювальних паличок і швидкостях годин, але закони фізики справедливі і самоузгоджені в будь-якій системі відліку. Так само спостерігачі в різних рамках відліку розходяться в думках про те, які електричні та магнітні поля і сили існують, але вони сходяться в думках про конкретні фізичні події.

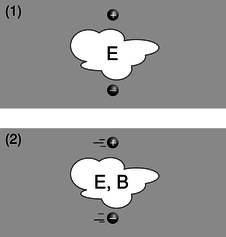
a/ Пара заряджених частинок, як видно в двох різних системах відліку.

Наприклад, на малюнку a /1 показано дві частинки з протилежними зарядами, які не рухаються в певний момент часу. Спостерігач у цій системі відліку каже, що навколо частинок є електричні поля, і прогнозує, що з часом частинки почнуть прискорюватися один до одного, врешті-решт стикаючись. Інший спостерігач, а /2, каже, що частинки рухаються. Цей спостерігач також пророкує, що частинки зіткнуться, але пояснює їх рух як електричним полем\(\mathbf{E}\), так і магнітним полем\(\mathbf{B}\). Як ми побачимо незабаром, магнітне поле потрібне для того, щоб підтримувати узгодженість між прогнозами, зробленими в двох системах відліку.

Щоб побачити, як це дійсно працює, нам потрібно знайти хороший простий приклад, який легко обчислити. Приклад, подібний до малюнка а, не простий у обробці, оскільки у другій системі відліку рухомі заряди створюють поля, які змінюються з часом у будь-якому заданому місці. Приклади, такі як цифра b, простіше, тому що відбувається постійний потік зарядів, і всі поля залишаються однаковими з часом. ¹ Чим примітна ця демонстрація, так це те, що електричних полів, що діють на електронний промінь, взагалі не може бути, так як загальна щільність заряду по всьому проводу дорівнює нулю. На відміну від малюнка a /2, цифра b чисто магнітна.

б/ Великий струм створюється шляхом замикання поперек висновків акумулятора. Рухомі заряди в дроті притягують рухомі заряди в електронному пучку, змушуючи електрони кривими.

Щоб зрозуміти, чому це повинно відбуватися на основі відносності, ми робимо математично ідеалізовану модель, показану на малюнку c.

с/Заряджена частинка і струм, помічені в двох різних системах відліку. Другий кадр рухається\(v\) зі швидкістю по відношенню до першого кадру, тому з них\(v\) віднімали всі швидкості. (Як обговорювалося в основному тексті, це лише приблизно правильно.)

Заряд сам по собі схожий на один з електронів в пучку вакуумної трубки фігури b, і пара рухомих, нескінченно довгих лінійних зарядів була замінена на дріт. Електрони в реальному дроті знаходяться в швидкому тепловому русі, а струм створюється тільки повільним дрейфом, накладеного на цей хаос. Друге відхилення від реальності полягає в тому, що в реальному експерименті протони знаходяться в стані спокою щодо стільниці, і саме електрони знаходяться в русі, але в с/1 ми маємо позитивні заряди, що рухаються в одному напрямку, а негативні - в інший бік. Якби ми хотіли, ми могли б побудувати третю систему відліку, в якій позитивні заряди були в спокої, що було б більше схоже на систему відліку, закріплену на стільниці в реальній демонстрації. Однак, як ми побачимо незабаром, кадри c /1 та c /2 розроблені таким чином, що їх особливо легко аналізувати. Важливо зазначити, що навіть незважаючи на те, що два лінійні заряди рухаються в протилежних напрямках, їх струми не скасовуються. Негативний заряд, що рухається вліво, робить струм, який йде вправо, тому в кадрі с/1 загальний струм вдвічі більше, ніж сприяв будь-який лінійний заряд.

Кадр 1 легко проаналізувати, оскільки щільність заряду двох лінійних зарядів скасовується, і електричне поле, яке відчуває одиночний заряд, тому дорівнює нулю:

\[\begin{equation*} \mathbf{E}_1 = 0 \end{equation*}\]

Тому в кадрі 1 будь-яка сила, яку відчуває самотній заряд, повинна бути віднесена виключно до магнетизму.

Кадр 2 показує, що ми побачили б, якби ми спостерігали все це з системи відліку рухається разом з самотнім зарядом. Чому щільність заряду також не скасовується в цьому кадрі? Ось де приходить відносність. Відносність говорить нам, що рухомі об'єкти здаються стиснутими до спостерігача, який не рухається разом з ними. Обидва лінійні заряди знаходяться в русі в обох системах відліку, але в кадрі 1 лінійні заряди рухалися з однаковими швидкостями, тому їх скорочення були рівними, а їх щільність заряду скасовувалася. У кадрі 2, однак, їх швидкості нерівні. Позитивні заряди рухаються повільніше, ніж в кадрі 1, тому в кадрі 2 вони менше скорочуються. Негативні заряди рухаються швидше, тому їх скорочення зараз більше. Оскільки щільність заряду не скасовується, в кадрі 2 є електричне поле, яке вказує на провід, залучаючи самотній заряд. Крім того, тяжіння, що відчувається самотнім зарядом, повинно бути чисто електричним, оскільки самотній заряд знаходиться в стані спокою в цій системі відліку, а магнітні ефекти виникають лише між рухомими зарядами та іншими рухомими зарядами. ²

Підводячи підсумок, кадр 1 відображає чисто магнітне тяжіння, в той час як в кадрі 2 він чисто електричний.

Тепер ми можемо обчислити силу в кадрі 2, і прирівнявши її до сили в кадрі 1, ми зможемо дізнатися, скільки магнітної сили виникає. Щоб математика була простою, і щоб не припускати занадто багато про ваші знання відносності, ми збираємося провести весь цей розрахунок в наближенні, де всі швидкості досить малі порівняно зі швидкістю світла. ³ Наприклад, якщо ми знайдемо такий вираз\((v/c)^2+(v/c)^4\), як, ми будемо вважати, що термін четвертого порядку незначний для порівняння. Це відоме як розрахунок «до провідного порядку в»\(v/c\). Насправді, я вже використовував наближення провідного порядку двічі, не кажучи так! Перший раз, коли я використовував його неявно, був на малюнку c, де я припустив, що швидкості двох лінійних зарядів були\(u-v\) і\(-u-v\). Релятивістські швидкості не просто поєднуються простим додаванням та відніманням, як це, але це ефект, який ми можемо ігнорувати в теперішньому наближенні. Друга спритність рук сталася, коли я заявив, що ми можемо прирівняти сили в двох рамках відліку. Сила, як час і відстань, спотворюється релятивістично, коли ми переходимо від однієї системи відліку до іншої. Знову ж таки, однак, це ефект, який ми можемо ігнорувати до бажаного рівня наближення.

\(\pm\lambda\)Дозволяти бути заряд на одиницю довжини кожного рядка заряду без релятивістського скорочення, тобто в кадрі, що рухається з цією лінією заряду. Використовуючи наближення\(\gamma=(1-v^2/c^2)^{-1/2}\approx 1+v^2/2c^2\) для\(v\ll c\), сумарний заряд на одиницю довжини в кадрі 2 дорівнює

\[\begin{align*} \lambda_{total,\ 2} &\approx \lambda\left[1+\frac{(u-v)^2}{2c^2}\right] -\lambda\left[1+\frac{(-u-v)^2}{2c^2}\right]\\ &= \frac{-2\lambda uv}{c^2} . \end{align*}\]

\(R\)Дозволяти відстань від лінійного заряду до самотнього заряду. Застосовуючи закон Гауса до циліндра радіуса,\(R\) зосередженого на лінійному заряді, ми виявимо, що величина електричного поля, яке відчуває одинокий заряд в кадрі 2, дорівнює

\[\begin{equation*} E = \frac{4k\lambda uv}{c^2R} , \end{equation*}\]

і сила, що діє на самотній заряд\(q\), є

\[\begin{equation*} F = \frac{4k\lambda quv}{c^2R} . \end{equation*}\]

У кадрі 1 струм є\(I=2\lambda_1 u\) (див. Завдання домашнього завдання 5), який ми можемо наблизити як\(I=2\lambda u\), оскільки струм, на відміну від\(\lambda_{total,\ 2}\), не зникає повністю без релятивістського ефекту. Магнітна сила на одиночному заряді за\(q\) рахунок струму\(I\) становить

\[\begin{equation*} F = \frac{2kI qv}{c^2R} . \end{equation*}\]

Обговорення Питання

◊ Вирішіть наступний парадокс щодо аргументу, наведеного в цьому розділі. Ми очікуємо, що в будь-який момент часу електрони в твердому тілі будуть пов'язані з протонами певним чином. Для простоти уявімо, що тверде речовина виготовляється з водню (який насправді стає металом в умовах дуже високого тиску). Атом водню складається з одного протона і одного електрона. Навіть якщо електрони рухаються і утворюють електричний струм, ми б уявили, що це було б як гра музичних стільців, протони як стільці, а електрони - як люди. Кожен електрон має протон, який є його «другом», принаймні на даний момент. Така ситуація показана на малюнку c /1. Як же тоді спостерігач може в іншому кадрі бачити електрони та протони як не спарені, як у c /2?

11.1.2 Магнітне поле

Визначення з точки зору сили на рухому частинку

З електрикою виявилося корисним визначити електричне поле, а не завжди працювати з точки зору електричних сил. Так само ми хочемо визначити магнітне поле,\(\mathbf{B}\). Давайте розглянемо результат попереднього підрозділу для розуміння. рівняння

\[\begin{equation*} F = \frac{2kI qv}{c^2R} \end{equation*}\]

показує, що коли ми ставимо рухомий заряд поблизу інших рухомих зарядів, на ньому є додаткова магнітна сила, крім будь-яких електричних сил, які можуть існувати. Рівняння для електричних сил завжди мають коефіцієнт попереду — постійна Кулона\(k\) називається постійною зв'язку для електричних сил.\(k\) Оскільки магнітні ефекти є релятивістськими за походженням, вони в кінцевому підсумку мають фактор\(k/c^2\) замість справедливого\(k\). У світі, де швидкість світла була нескінченною, релятивістські ефекти, включаючи магнетизм, були б відсутні, а константа зв'язку для магнетизму дорівнювала б нулю. Симпатичною особливістю метричної системи є те, що ми маємо\(k/c^2=10^{-7}\ \text{N}\cdot\text{s}^2/\text{C}^2\) саме, як питання визначення.

Наївно ми могли б спробувати працювати за аналогією з електричним полем, і визначити магнітне поле як магнітну силу на одиницю заряду. Однак, якщо ми думаємо про самотній заряд в нашому прикладі як про тестовий заряд, то виявимо, що такий підхід не вдається, оскільки сила залежить не тільки від заряду тестової частинки\(v\), а й від її швидкості. Хоча ми проводили розрахунки лише для випадку, коли частка рухалася паралельно проводу, загалом ця швидкість є вектором, v, в трьох вимірах. Ми також можемо передбачити, що магнітне поле буде вектором. Електричні та гравітаційні поля є векторами, і ми очікуємо інтуїтивно, спираючись на наш досвід роботи з магнітними компасами, що магнітне поле має певний напрямок у просторі. Крім того, реверсування струму\(I\) в нашому прикладі змінило б силу, що мало б сенс лише в тому випадку, якби магнітне поле мало напрямок у просторі, який можна було б змінити. Підводячи підсумок, ми вважаємо, що повинен бути вектор магнітного поля B, а сила на тестовій частинці, що рухається через магнітне поле, пропорційна як вектору B, так і власному вектору частинки v. Іншими словами, вектор магнітної сили F знаходить якимось векторним множенням векторів v і B. Однак, як доведено на сторінці 912, існує лише один фізично корисний спосіб визначення такого множення, який є перехресним добутком.

Тому ми визначаємо вектор магнітного поля B як вектор, який визначає силу на заряджену частинку відповідно до наступного правила:

\[\begin{equation*} \mathbf{F} = q\mathbf{v}\times\mathbf{B} \text{[definition of the magnetic field]} \end{equation*}\]

d/Правостороння залежність між швидкістю позитивно зарядженої частинки, магнітним полем, через яке вона рухається, і магнітною силою на ній.

З цього визначення ми бачимо, що одиниці магнітного поля є\(\text{N}\cdot\text{s}/\text{C}\cdot\text{m}\), які зазвичай скорочуються як тесла,\(1\ \text{T}=1\ \text{N}\cdot\text{s}/\text{C}\cdot\text{m}\). Визначення має на увазі правосторонній зв'язок між векторами, цифра d, якщо\(q\) заряд позитивний, і протилежну передачу, якщо він негативний.

e/Одиниця магнітного поля, тесла, названа на честь сербсько-американського винахідника Ніколи Тесла.

Це не просто визначення, а сміливий прогноз! Чи правда, що для будь-якої точки простору ми завжди можемо знайти вектор B, який успішно прогнозує силу на будь-яку проходить частку, незалежно від її заряду і вектора швидкості? Так — не очевидно, що це можна зробити, але експерименти перевіряють, що це може. Як? Ну, наприклад, поперечний добуток паралельних векторів дорівнює нулю, тому ми можемо спробувати частинки, що рухаються в різних напрямках, і полювати за напрямком, який виробляє нульову силу; Вектор B лежить уздовж цієї лінії, або в тому ж напрямку частинка рухалася, або в протилежному. Потім ми можемо повернутися до наших даних з одного з інших випадків, коли сила була ненульовою, і використовувати її, щоб вибрати між цими двома напрямками і знайти величину вектора B. Потім ми могли б перевірити, що цей вектор дав правильні прогнози сили в різних інших випадках.

Навіть з цим емпіричним запевненням значення цього рівняння не є інтуїтивно прозорим, і в більшості випадків не практично вимірювати магнітне поле таким чином. З цих причин давайте розглянемо альтернативний метод визначення магнітного поля, який, хоча і не настільки фундаментальний або математично простий, може бути більш привабливим.

Визначення з точки зору крутного моменту на диполі

Стрілка компаса в магнітному полі відчуває крутний момент, який має тенденцію вирівняти його з полем. Це так само, як поведінка електричного диполя в електричному полі, тому ми вважаємо стрілку компаса магнітним диполем. У підрозділі 10.1.3 на стор. 567 ми дали альтернативне визначення електричного поля з точки зору крутного моменту на електричному диполі.

Однак, щоб визначити напруженість магнітного поля, нам потрібен певний спосіб визначення сили тестового диполя, тобто нам потрібно визначення магнітного дипольного моменту. Ми могли б використовувати залізний постійний магніт, побудований за певними специфікаціями, але такий об'єкт дійсно є надзвичайно складною системою, що складається з безлічі атомів заліза, лише деякі з яких вирівняні між собою. Більш фундаментальним стандартним диполем є квадратний струмовий контур. Це може бути мало резистивний ланцюг, що складається з квадрата дроти замикання через батарею, f.

f/Стандартний диполь, виготовлений з квадратної петлі дротяного замикання через батарею. Він діє дуже схоже на стрижневий магніт, але його міцність легше кількісно оцінити.

Застосовуючи\(\mathbf{F}=\mathbf{v}\times\mathbf{B}\), ми виявляємо, що така петля при розміщенні в магнітному полі, г, відчуває крутний момент, який прагне вирівняти площину так, щоб її внутрішня «грань» вказувала в певному напрямку.

г/Диполь має тенденцію вирівнюватися з навколишнім магнітним полем.

Оскільки петля симетрична, це не хвилює, якщо ми обертаємо її, як колесо, не змінюючи площину, в якій вона лежить. Саме цей бажаний напрямок звернення ми в кінцевому підсумку будемо використовувати як наше альтернативне визначення магнітного поля.

Якщо шлейф знаходиться поза співвідношенням з полем, крутний момент на ньому пропорційний величині струму, а також внутрішньої площі петлі. Пропорційність струму має сенс, так як магнітні сили - це взаємодія між рухомими зарядами, а струм - міра руху заряду. Пропорційність площі петлі також не важко зрозуміти, оскільки збільшення довжини сторін квадрата збільшує як кількість заряду, що міститься в цій круговій «річці», так і величину важеля, що подається для виготовлення крутного моменту. Дві окремі фізичні причини пропорційності довжині призводять до загальної пропорційності довжині в квадраті, яка така ж, як площа петлі. З цих причин ми визначаємо магнітний дипольний момент квадратного контуру струму як

\[\begin{equation*} \mathbf{m} = I\mathbf{A} , \end{equation*}\]

де напрямок векторів визначається як показано на малюнку h.

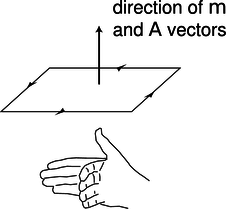
h/Вектори m та A.

Тепер можна дати альтернативне визначення магнітного поля:

Вектор магнітного поля, B, в будь-якому місці в просторі визначається шляхом спостереження за крутним моментом, що чиниться на магнітному випробувальному диполі,\(\mathbf{m}_{t}\) що складається з квадратного контуру струму. Величина поля дорівнює

\[\begin{equation*} |\mathbf{B}| = \frac{\tau}{|\mathbf{m}_{t}|\sin\theta} , \end{equation*}\]

де\(\theta\) - кут між дипольним вектором і полем. Це еквівалентно векторному перехресному добутку\(\boldsymbol{\tau}=\mathbf{m}_t\times\mathbf{B}\).

Давайте покажемо, що це узгоджується з попереднім визначенням, використовуючи геометрію, зображену на малюнку i.

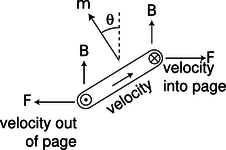
i/Крутний момент на контурі струму в магнітному полі. Струм виходить зі сторінки, переходить, повертається на сторінку, а потім назад через інший бік в приховану сторону циклу.

Вектор швидкості, який вказує на сторінку та поза нею, показаний за допомогою конвенції, визначеної на малюнку j.

j/Вектор, що виходить зі сторінки, відображається кінчиком наконечника стрілки. Вектор, що йде на сторінку, зображується за допомогою хвостових пір'їв стрілки.

Нехай мобільні носії заряду в дроті мають лінійну щільність\(\lambda\), а сторони петлі нехай мають довжину\(h\), так що у нас є\(I=\lambda v\), і\(m=h^2\lambda v\). Єдиний незникаючий крутний момент походить від сил на лівій і правій стороні. Струми в цих боках перпендикулярні полю, тому величина перехресного\(\mathbf{F}=q\mathbf{v}\times\mathbf{B}\) добутку просто\(|\mathbf{F}|=qvB\). Крутний момент, що подається кожною з цих сил\(\mathbf{r}\times\mathbf{F}\), є тим, де важіль важеля\(\mathbf{r}\) має довжину\(h/2\), і робить кут\(\theta\) по відношенню до вектора сили. Величина загального крутного моменту, що діє на петлю, тому

\[\begin{align*} |\boldsymbol{\tau}| &=2\frac{h}{2}|\mathbf{F}|\sin\theta \\ &=h\:qvB\:\sin\theta ,\\ \text{and substituting $q=\lambda h$ and $v=m/h^2\lambda$, we have}\\ |\boldsymbol{\tau}| &= h\:\lambda h\:\frac{m}{h^2\lambda} B\sin\theta \\ &=m B\sin\theta ,\\ \end{align*}\]

що узгоджується з другим визначенням поля.

Безсумнівно, вам здається штучним, що ми обговорювали диполі тільки у вигляді квадратної петлі струму. Наприклад, постійний магніт виготовлений з атомних диполів, а атоми не квадратні! Однак виявляється, що форма не має значення. Щоб зрозуміти, чому це так, розглянемо адитивне властивість областей і дипольних моментів, показане на малюнку k.

k/дипольні вектори можуть бути додані.

Кожен з квадратних диполів має дипольний момент, який вказує на сторінку. Коли вони розміщені поруч, струми в прилеглих сторонам скасовуються, тому вони еквівалентні одній прямокутній петлі з подвоєною площею. Ми можемо розбити будь-яку неправильну форму на маленькі квадрати, як показано на малюнку l, тому дипольний момент будь-якого плоского контуру струму можна обчислити виходячи з його площі, незалежно від його форми.

л/Нерегулярну петлю можна розбити на маленькі квадрати.

Приклад 1: Магнітний дипольний момент атома

Давайте зробимо на порядок оцінку магнітного дипольного моменту атома. Атом водню близько\(10^{-10}\) m в діаметрі, а електрон рухається зі швидкістю близько\(10^{-2} c\). Ми не знаємо форми орбіти, і справді виявляється, що згідно з принципами квантової механіки електрон навіть не має чітко визначеної орбіти, але якщо ми сміливі, ми все одно можемо оцінити дипольний момент, використовуючи площу поперечного перерізу атома, яка буде на порядку \((10^{-10}\ \text{m})^2=10^{-20}\ \text{m}^2\). Електрон - це одиночна частинка, а не стійкий струм, але знову ж таки накидаємо обережність до вітрів, і оцінюємо струм\(e/\Delta t\), який він створює\(\Delta t\), як, де, час для однієї орбіти, можна оцінити, діливши розмір атома на швидкість електрона. (Це лише приблизна оцінка, і ми не знаємо форми орбіти, тому було б нерозумно, наприклад, возитися з множенням діаметра на\(\pi\) основі нашої інтуїтивної візуалізації електрона як рухається по колу кола.) Результат для дипольного моменту є\(m\sim10^{-23}\ \text{A}\!\cdot\!\text{m}^2\). Чи повинні ми бути вражені тим, наскільки малий цей дипольний момент, або наскільки він великий, враховуючи, що він робиться одним атомом? Дуже великі або дуже малі цифри ніколи не дуже цікаві самі по собі. Щоб отримати відчуття того, що вони означають, нам потрібно порівняти їх з чимось іншим. Цікавим порівнянням тут є думка з точки зору загальної кількості атомів у типовому об'єкті, яка може бути на порядку\(10^{26}\) (число Авогадро). Припустимо, у нас було стільки атомів, з їхніми моментами всі вирівняні. Загальний дипольний момент буде на порядку\(10^3\ \text{A}\!\cdot\!\text{m}^2\), що є досить великим числом. Щоб отримати дипольний момент цього сильного за допомогою пристроїв людського масштабу, нам доведеться відправити тисячу ампер струму через петлю дроту на один квадратний метр! Тут слід отримати розуміння того, що навіть у постійному магніті ми не повинні мати всі атоми ідеально вирівняні, тому що це спричинить більш вражаючі магнітні ефекти, ніж ми насправді спостерігаємо. Мабуть, майже всі атоми в такому магніті орієнтовані випадково, і не сприяють дипольному моменту магніту.

м/Магнітний малюнок поля навколо стрижневого магніту створюється шляхом накладання дипольних полів окремих атомів заліза. Грубо кажучи, схоже на поле одного великого диполя, особливо далі від магніту. Однак ближче ви можете побачити натяк на прямокутну форму магніту. Картина була зроблена шляхом розміщення залізних пилок на аркуші паперу, а потім піднесення магніту вгору.

Питання для обговорення

◊ Фізична ситуація, показана на малюнку c на сторінці 648, була повністю проаналізована з точки зору сил. Тепер повернемося назад і подумаємо про це з точки зору полів. Заряд сам по собі над проводом схожий на тестовий заряд, який використовується для визначення магнітних і електричних полів, створених дротом. У малюнках c /1 і c /2 є поля, які є чисто електричними або чисто магнітними? Чи є поля, які є сумішшю\(\mathbf{E}\) і\(\mathbf{B}\)? Як це порівнюється з силами?

◊ Продовжуючи аналіз, розпочатий в дискусійному питанні А, чи можемо ми придумати сценарій із залученням деяких заряджених частинок таким чином, що поля є чисто магнітними в одному кадрі відліку, але сумішшю\(\mathbf{E}\) та\(\mathbf{B}\) в іншому кадрі? Як щодо прикладу, де поля чисто електричні в одному кадрі, але змішані в іншому? Або приклад, коли поля чисто електричні в одному кадрі, а чисто магнітні в іншому?

11.1.3 Деякі програми

Приклад 2: Магнітна левітація

n/Приклад 2. На малюнку n невеликий постійний магніт у формі диска застряг на стороні батареї, а дріт вільно обхоплюється навколо батареї, замикаючи його. По проводу протікає великий струм. Електрони, що рухаються по дроту, відчувають силу від магнітного поля, створеного постійним магнітом, і ця сила левітує дріт. По фотографії можна знайти напрямок магнітного поля, зробленого постійним магнітом. Електрони в мідному дроті негативно заряджені, тому вони перетікають від негативної (плоскої) клеми акумулятора до плюсової клеми (тієї, що з шишкою, спереду). Коли електрони проходять повз постійного магніту, ми можемо уявити, що вони відчують поле або до магніту, або подалі від нього, залежно від того, яким чином магніт був перевернутий, коли він був застряг на акумуляторі. За правилом праворуч (рис. d на стор. 651) поле повинно бути в сторону батареї.

Приклад 3: Ефекти нервової системи під час МРТ-скану<</th>
Під час МРТ голови нервова система пацієнта піддається впливу інтенсивних магнітних полів, а в нервах рухаються іони. Утворені сили на іони можуть викликати такі симптоми, як вертиго.

Приклад 4: Кругова орбіта

Магнітна сила завжди перпендикулярна руху частинки, тому вона ніколи не може виконати жодної роботи, а заряджена частинка, що рухається через магнітне поле, не відчуває жодних змін своєї кінетичної енергії: її вектор швидкості може змінювати свій напрямок, але не його величину. Якщо вектор швидкості спочатку перпендикулярний полю, то крива його руху залишиться в площині, перпендикулярній полю, тому величина магнітної сили на ньому залишиться колишньою. Коли об'єкт відчуває силу з постійною величиною, яка завжди перпендикулярна напрямку його руху, результатом є те, що він рухається по колу. o/Магнітні сили змушують пучок електронів рухатися по колу. На малюнку o зображений пучок електронів в сферичній вакуумній трубці. На верхньому фото промінь випромінюється біля правого боку труби, і рухається прямо вгору. На нижній фотографії магнітне поле накладено електромагнітом, що оточує вакуумну трубку; амперметр праворуч показує, що струм через електромагніт тепер ненульовий. Спостерігаємо, що промінь зігнутий в коло.

самостійна перевірка:

Вивести напрямок магнітного поля. Не забувайте, що промінь складається з електронів, які негативно заряджені!

(відповідь у зворотному боці PDF-версії книги)

Завдання домашнього завдання 12 - кількісний аналіз кругових орбіт.

Приклад 5. Фільтр швидкості

Припустимо, ви бачите електронний пучок на малюнку o, і хочете визначити, наскільки швидко йдуть електрони. Ви, звичайно, не можете зробити це за допомогою секундоміра! Фізики також можуть зіткнутися з ситуаціями, коли у них є промінь невідомих заряджених частинок, і вони навіть не знають своїх зарядів. Це сталося, наприклад, коли були виявлені альфа- і бета-випромінювання. Одне з рішень цієї проблеми спирається на те, що сила, яку відчуває заряджена частинка в електричному полі\(\mathbf{F}_E=q\mathbf{E}\), не залежить від її швидкості, але сила, обумовлена магнітним полем\(\mathbf{F}_B=q\mathbf{v}\times\mathbf{B}\), не є. Можна направити пучок заряджених частинок через простір, що містить як електричне, так і магнітне поле, налаштовуючи поля так, що дві сили відмінно скасуються для певної швидкості. Зверніть увагу, що оскільки обидві сили пропорційні заряду частинок, скасування не залежить від заряду. Такий фільтр швидкості може використовуватися або для визначення швидкості невідомого пучка або частинок, або для вибору з пучка частинок тільки тих, що мають швидкості в певному бажаному діапазоні. Завдання домашнього завдання 7 - це аналіз цього додатка.

11.1.4 Немає магнітних монополів

Якби ви могли грати з жменькою електричних диполів і жменькою барних магнітів, вони виглядали б дуже схожими. Наприклад, пара стрижневих магнітів хоче вирівняти себе головою до хвоста, а пара електричних диполів робить те ж саме. (На жаль, не так просто зробити постійний електричний диполь, який можна обробляти так, оскільки заряд має тенденцію до витоку.)

Однак, врешті-решт, ви помітите важливу різницю між двома типами об'єктів. Електричні диполі можуть бути розбиті, утворюючи ізольовані позитивні заряди та негативні заряди. Двосторонній пристрій можна розбити на частини, які не є двосторонніми. Але якщо розбити стрижневий магніт навпіл, р, ви виявите, що ви просто зробили два менших двосторонніх предмета.

p/ Ви не можете ізолювати полюси магніту, розбивши його навпіл.

Причина такої поведінки не важко божественна від нашої мікроскопічної картини постійних залізних магнітів. Електричний диполь має додатковий позитивний «матеріал», зосереджений на одному кінці, і додатковий негативний в іншому. Стрічковий магніт, з іншого боку, отримує свої магнітні властивості не від дисбалансу магнітних «речей» на двох кінцях, а від орієнтації обертання його електронів. Один кінець - це той, з якого ми могли б дивитися вниз по осі і побачити електрони, що обертаються за годинниковою стрілкою, а інший - той, з якого вони, здається, йдуть проти годинникової стрілки. Немає різниці між «штучкою» в одному кінці магніту і на іншому, q.

q/Магнітний диполь виготовлений з інших диполів, а не з монополів.

Нікому ніколи не вдавалося ізолювати один магнітний полюс. Технічною мовою ми говоримо, що магнітних монополів, схоже, не існує. Електричні монополі існують - ось що таке заряди.

Електричні та магнітні сили багато в чому схожі. Обидва діють на відстані, обидва можуть бути привабливими або відразливими, і обидва тісно пов'язані з властивістю матерії, яка називається зарядом. (Нагадаємо, що магнетизм - це взаємодія між рухомими зарядами.) Естетичні почуття фізиків вже давно ображалися тому, що ця уявна симетрія порушена існуванням електричних монополів і відсутністю магнітних. Можливо, існує якась екзотична форма матерії, що складається з частинок, які є магнітними монополями. Якби такі частинки можна було знайти в космічних променях або місячних породах, це було б свідченням того, що явна асиметрія була лише асиметрією в складі Всесвіту, а не в законі фізики. З цих, безумовно, суб'єктивних причин було кілька пошуків магнітних монополів. Були проведені експерименти з негативними результатами для пошуку магнітних монополів, вбудованих у звичайну речовину. Радянські фізики в 1960-х роках висловлювали захоплюючі твердження про те, що створювали і виявляли магнітні монополя в прискорювачах частинок, але не було успіху в спробах відтворити результати там або на інших прискорювачах. Останній пошук магнітних монополів, зроблений шляхом повторного аналізу даних з пошуку верхнього кварку в Fermilab, не виявив кандидатів, що показує, що або монополі не існують в природі, або вони надзвичайно масивні і, таким чином, важко створити в прискорювачах.

r/Магнітні поля не мають джерел або раковин.

Неіснування магнітних монополів означає, що на відміну від електричного поля, магнітного, ніколи не може мати джерел або потоків. Вектори магнітного поля ведуть в шляхах, які петлять назад на себе, ніколи не сходяться або не розходяться в точці, як у полах, показаних на малюнку r. Тому закон Гауса для магнетизму набагато простіший, ніж закон Гауса для електричних полів:

\[\begin{equation*} \Phi_B = \sum \mathbf{B}_j\cdot\mathbf{A}_j = 0 \end{equation*}\]

Магнітний потік через будь-яку замкнуту поверхню дорівнює нулю.

самостійна перевірка:

Намалюйте гаусову поверхню на електричному дипольному полі фігури r, яке має ненульовий електричний потік через нього, а потім намалюйте аналогічну поверхню на малюнку магнітного поля. Що відбувається?

(відповідь у зворотному боці PDF-версії книги)

Приклад 6: Поле дроти

\(\triangleright\)На сторінці 650 ми показали, що довгий прямий провід, що несе струм,\(I\) надає магнітну силу \[\begin{equation*} F = \frac{2 kIqv}{ c^2 R} \end{equation*}\] на частинці з зарядом, що\(q\) рухається паралельно проводу зі швидкістю\(v\). Що ж тоді являє собою магнітне поле дроту? s/Приклад 6. \(\triangleright\)Порівнюючи рівняння вище з першим визначенням магнітного поля\(\mathbf{F}=\mathbf{v}\times\mathbf{B}\), виявляється, що магнітне поле - це таке\(1/ R\), яке падає\(R\) подібно, де відстань від дроту. Однак визначити напрямок вектора поля не так-то просто. Є дві інші осі, вздовж яких частка могла рухатися, і метод грубої сили полягав би у проведенні релятивістських розрахунків і для цих випадків. Хоча це, ймовірно, буде достатньо інформації, щоб визначити поле, ми не хочемо робити стільки роботи. Замість цього давайте розглянемо, які є можливості. Поле не може бути паралельним проводу, тому що поперечний добуток зникає, коли два вектори паралельні, і все ж ми знаємо з випадку, який ми проаналізували, що сила не зникає, коли частинка рухається паралельно проводу. Інші дві можливості, які узгоджуються з симетрією задачі, показані на малюнку s. Один схожий на пляшкову щітку, а інший - як котушка нитки. Однак малюнок пензля для пляшок порушує закон Гауса за магнетизм. Якби ми зробили циліндричну гауссову поверхню з її віссю, що збігається з дротом, потік через неї не дорівнював би нулю. Тому ми робимо висновок, що візерунок котушки нитки є правильним. ^4 Оскільки частка в нашому прикладі рухалася перпендикулярно полю, ми маємо\(| F|=|q|| v|| B|\), так \[\begin{align*} | B| &= \frac{| F|}{|q| | v|} \\ &= \frac{2 kI}{ c^2 R}\\ \end{align*}\]

11.1.5 Симетрія і вправність

Уявіть, що ви встановлюєте радіоконтакт з інопланетянином на іншій планеті. Жоден з вас навіть не знає, де знаходиться інша планета, і ви не можете встановити жодних орієнтирів, які ви обидва розпізнаєте. Вам вдається вивчити зовсім небагато мов один одного, але ви впадаєте в глухий кут, коли намагаєтеся встановити визначення лівого і правого (або, еквівалентно, за годинниковою стрілкою і проти годинникової стрілки). Чи є спосіб це зробити?

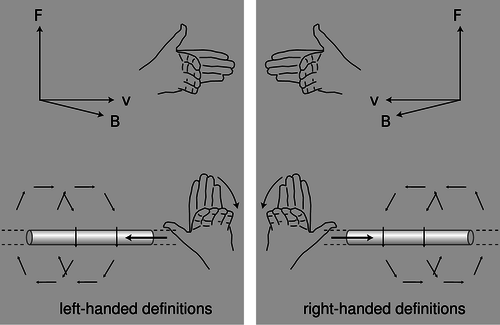
t/Лівша і правша визначення.

Якби був спосіб зробити це без прив'язки до зовнішніх орієнтирів, то це означало б, що самі закони фізики були асиметричними, що було б дивно. Чому вони повинні відрізняти ліве від правого? Гравітаційне поле, що оточує зірку або планету, виглядає однаково в дзеркалі, і те ж саме стосується електричних полів. Однак малюнки магнітного поля, показані на малюнку s, здається, порушують цей принцип. Чи могли б ви використовувати ці шаблони, щоб пояснити ліворуч і праворуч інопланетянина? Ні. Якщо озирнутися назад на визначення магнітного поля, то воно також містить посилання на передачу: напрямок векторного перехресного добутку. Інопланетяни, можливо, змінили своє визначення магнітного поля, і в цьому випадку їх малюнки польових візерунків виглядали б як дзеркальні зображення наших, як на лівій панелі малюнка t.

До середини двадцятого століття фізики припускали, що будь-який розумний набір фізичних законів повинен мати такий вид симетрії між лівим і правим.

u / In this scene from Swan Lake, the the choreography has a symmetry with respect to left and right.

An asymmetry would be grotesque. Whatever their aesthetic feelings, they had to change their opinions about reality when experiments by C.S. Wu et al. showed that the weak nuclear force violates right-left symmetry!

v / C.S. Wu

It is still a mystery why right-left symmetry is observed so scrupulously in general, but is violated by one particular type of physical process.

Contributors

Template:ContribCrowell