10.2: Паралельні та послідовні схеми
- Page ID
- 73570
У розділі 9.1 ми обмежилися відносно простими схемами, по суті не що інше, як акумулятор і одна лампочка. Мета цієї глави - познайомити вас з більш складними схемами, що містять кілька резисторів або джерел напруги послідовно, паралельно або обидва.
9.2.1 Схеми
Я бачу шахову позицію; Каспаров бачить цікаву варіацію Руя Лопеса. Для непосвячених схема може виглядати так само незрозумілою, як ієрогліфи майя, але навіть трохи тренування очей може пройти довгий шлях до того, щоб зробити його значення стрибнути зі сторінки. Схема - це стилізоване і спрощене креслення схеми. Мета полягає в тому, щоб усунути якомога більше нерелевантних особливостей, щоб відповідні було легше підібрати.

а/1. Неправильно: форми проводів не мають значення. Неправильно: Слід використовувати прямі кути. Неправильно: Простий візерунок зроблений так, щоб виглядати незнайомим і складним. Право.
Прикладом нерелевантної особливості є фізична форма, довжина і діаметр дроту. Майже у всіх схемах хорошим наближенням є припустити, що дроти є ідеальними провідниками, так що будь-який шматок дроту, безперебійний іншими компонентами, має постійну напругу протягом усього нього. Зміна довжини проводу, наприклад, не змінює цього факту. (Звичайно, якби ми використовували милі та милі дроту, як у телефонній лінії, опір дроту почне складатися, і його довжина почне мати значення.) Форми проводів також не мають значення, тому малюємо їх стандартизованими, стилізованими формами, виконаними тільки з вертикальних і горизонтальних ліній з прямокутними вигинами в них. Це призводить до того, що подібні схеми виглядають більш схожими і допомагають нам розпізнавати знайомі зразки, так само як слова в газеті легше розпізнати, ніж рукописні. На малюнку а показані деякі приклади цих понять.

б/Дві затінені області, що мають форму літери «E», є обома областями постійної напруги.
Найважливішим першим кроком у навчанні читати схеми є навчитися розпізнавати суміжні шматки дроту, які повинні мати постійну напругу на всьому протязі. Наприклад, на малюнку b два затінених E-образних шматка дроту повинні мати постійну напругу. Це фокусує нашу увагу на двох основних невідомих, які ми хотіли б передбачити: напруга лівого E та напруга тієї, що знаходиться праворуч.
9.2.2 Паралельні опори та правило з'єднання
Одним з найпростіших прикладів для аналізу є паралельна ланцюг опору, прикладом якої була цифра b. Загалом у нас можуть бути нерівні\(R_1\) опори і\(R_2\), як в c /1. Оскільки в ланцюзі всього дві області постійної напруги, c /2, всі три компоненти мають однакову різницю напруг на них. Акумулятор зазвичай вдається підтримувати різницю напруги на собі, для яких він був розроблений, тому падіння\(\Delta V_2\) напруги\(\Delta V_1\) і на резисторах повинні обидва дорівнювати напрузі акумулятора:
Таким чином, кожен опір відчуває ту саму різницю напруги, як якщо б він був єдиним в ланцюзі, і закон Ома говорить нам, що кількість струму, що протікає через кожен з них, також така ж, як це було б в ланцюзі з одним резистором. Саме тому побутові електричні ланцюги проводяться паралельно. Ми хочемо, щоб кожен прилад працював однаково, незалежно від того, чи інші прилади підключені або відключені, ввімкнені або вимкнені. (Електрична компанія, звичайно, не використовує акумулятори, але наш аналіз був би однаковим для будь-якого пристрою, який підтримує постійну напругу.)

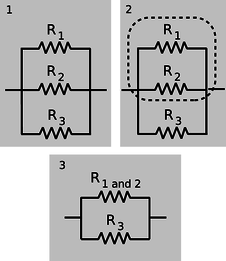
з/ 1. Два резистора паралельно. Є дві області постійної напруги. Струм, який виходить з батареї, розщеплюється між двома резисторами, а пізніше возз'єднується. Два резистора паралельно можна розглядати як один резистор з меншим значенням опору.
Звичайно, електрична компанія може сказати, коли ми включаємо кожне світло в будинку. Звідки вони знають? Відповідь полягає в тому, що ми проводимо більше струму. Кожен опір тягне певну кількість струму, а сума, яку потрібно подати, є сумою двох окремих струмів. Течія схожа на річку, яка розщеплюється навпіл, c /3, а потім возз'єднується. Сумарний струм дорівнює
Це приклад загального факту, який називається правилом з'єднання:
У будь-якій схемі, яка не зберігає або не звільняє заряд, збереження заряду означає, що загальний струм, що витікає з будь-якого переходу, повинен бути таким же, як і загальний протікає.
Повертаючись до аналізу нашої схеми, застосовуємо закон Ома до кожного опору, в результаті чого
Що стосується електричної компанії, то весь ваш будинок - це лише один резистор з деяким опором\(R\), який називається еквівалентним опором. Вони б написали закон Ома як
з якого ми можемо визначити еквівалентний опір шляхом порівняння з попереднім виразом:
[еквівалентний опір двох резисторів паралельно]
Два резистора паралельно, с/4, еквівалентні одному резистору зі значенням, заданим вищевказаним рівнянням.
| Приклад 10: Дві лампи на одній побутовій схемі |
|---|
| \(\triangleright\)Ви включаєте дві лампи, які знаходяться на одній побутовій схемі. Кожен з них має опір 1 Ом. Що таке еквівалентний опір, і як порівнюється розсіювання потужності з корпусом однієї лампи? \(\triangleright\)Еквівалентний опір двох ламп паралельно дорівнює \[\begin{align*} R &= \left(\frac{1}{ R_1}+\frac{1}{ R_2}\right)^{-1} \\ &= \left(\frac{1}{1\ \Omega}+\frac{1}{1\ \Omega}\right)^{-1} \\ &= \left(1\ \Omega^{-1} + 1\ \Omega^{-1}\right)^{-1} \\ &= \left(2\ \Omega^{-1}\right)^{-1} \\ &= \text{0.5}\ \Omega \end{align*}\] Різниця напруг по всій схемі - це завжди 110 В, встановлена електричною компанією (це змінний струм, але це не має значення). Опір всієї схеми було скорочено навпіл, включивши другу лампу, тому фіксована кількість напруги буде виробляти вдвічі більше струму. Двічі струм, що протікає через ту ж різницю напруги, означає вдвічі більше розсіювання потужності, що має сенс. |
Різання в половині опору дивує багатьох студентів, оскільки ми «додаємо більше опору» ланцюгу, ставлячи другу лампу. Чому еквівалентне опір виходить менше опору однієї лампи? Це випадок, коли чисто словесні міркування можуть вводити в оману. Резистивний елемент ланцюга, такий як нитка розжарювання лампочки, не є ні ідеальним ізолятором, ні ідеальним провідником. Замість того, щоб аналізувати цей тип ланцюга з точки зору «резисторів», тобто часткових ізоляторів, ми могли б говорити про «провідники». Цей приклад тоді здавався б розумним, оскільки ми «додали більше провідності», але тоді було б неправильне очікування щодо випадку резисторів послідовно, розглянутих у наступному розділі.
Можливо, більш продуктивним способом мислення про нього є використання механічної інтуїції. За аналогією ваші ніздрі протистоять потоку повітря через них, але наявність двох ніздрів дозволяє дихати вдвічі легше.
| Приклад 11: Три резистора паралельно |
|---|
| \(\triangleright\)Що станеться, якщо у нас паралельно три і більше резисторів?
d/ Три резистора паралельно.
\(\triangleright\)Це важливий приклад, оскільки рішення передбачає важливу техніку для розуміння схем: розбивання їх на менші частини та спрощення цих частин. У ланцюзі d /1, з трьома резисторами паралельно, ми можемо думати про два резистори як утворюють один великий резистор, d /2, з еквівалентним опором \[\begin{equation*} R_{12} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}\right)^{-1} . \end{equation*}\] Потім ми можемо спростити схему, як показано в d /3, так що вона містить лише два опори. Еквівалентне опір всієї ланцюга потім задається \[\begin{equation*} R_{123} = \left(\frac{1}{ R_{12}}+\frac{1}{ R_3}\right)^{-1} . \end{equation*}\] Підставляючи\(R_{12}\) і спрощуючи, знаходимо результат \[\begin{equation*} R_{123} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}+\frac{1}{ R_3}\right)^{-1} , \end{equation*}\] про який ви, напевно, могли здогадатися. Цікавим моментом тут є концепція розділяй і володарюй, а не математичний результат. |
| Приклад 12: Довільне число однакових резисторів паралельно |
|---|
| \(\triangleright\)Яке опір\(N\) однакових резисторів паралельно? \(\triangleright\)Узагальнюючи результати для двох і трьох резисторів, маємо \[\begin{equation*} R_{N} = \left(\frac{1}{ R_1}+\frac{1}{ R_2}+...\right)^{-1} , \end{equation*}\] де «...» означає, що в суму входять всі резистори. Якщо всі резистори ідентичні, це стає \[\begin{align*} R_{N} &= \left(\frac{ N}{ R}\right)^{-1} \\ &= \frac{ R}{ N} \end{align*}\] |
| Приклад 13: Залежність опору від площі поперечного перерізу |
|---|
|
e/Об'єднання чотирьох резисторів паралельно еквівалентно виготовленню одного резистора з однаковою довжиною, але в чотири рази більшою площею поперечного перерізу. В результаті вийде зробити резистор з однією чвертю опору.
Ми коротко натякнули на те, що електричний опір об'єкта залежить від його розмірів і форми, але тепер ми готові почати робити більш математичні твердження про нього. Як пропонує малюнок е, збільшення площі поперечного перерізу резисторів еквівалентно додаванню більшої кількості резисторів паралельно, що призведе до загального зниження опору. Будь-який справжній резистор з прямими, паралельними сторонами може бути розрізаний на велику кількість шматків, кожна з площею поперечного перерізу, скажімо, 1\(\mu \text{m}^2\). Число таких зрізів пропорційно загальній площі поперечного перерізу резистора, і, застосувавши результат попереднього прикладу, ми виявимо, що опір об'єкта обернено пропорційний його площі поперечного перерізу.\(N\)
f/Жирова труба має менший опір, ніж худа труба.
Аналогічне співвідношення має для водопровідних труб, саме тому магістральні лінії високого потоку повинні мати великі площі поперечного перерізу. Щоб багато води (струму) протікала через тонку трубу, нам знадобиться непрактично велика різниця тиску (напруги). |
| Приклад 14: Неправильні показання з вольтметра |
|---|
|
г/Вольтметр - це дійсно амперметр з внутрішнім резистором. Коли ми вимірюємо різницю напруги на резисторі, 1, ми дійсно будуємо паралельний ланцюг опору, 2.
Вольтметр - це насправді просто амперметр з внутрішнім резистором, і ми використовуємо вольтметр паралельно з тим, що ми намагаємося виміряти різницю напруги. Це означає, що кожного разу, коли ми вимірюємо падіння напруги на резисторі, ми по суті ставимо два резистори паралельно. Амперметр всередині вольтметра можна проігнорувати з метою аналізу того, як протікає струм в ланцюзі, так як це по суті всього лише якийсь намотаний провід з дуже низьким опором. Тепер, якщо ми проводимо це вимірювання на резисторі, який є частиною більшої схеми, ми змінили поведінку схеми через наш акт вимірювання. Це так, ніби ми змінили схему, замінивши опір на\(R\) менший еквівалентний опір\(R\) і\(R_v\) паралельно. Саме з цієї причини вольтметри будуються з максимально можливим внутрішнім опором. Як числовий приклад, якщо ми використовуємо вольтметр з внутрішнім опором 1\(M\Omega \) для вимірювання падіння напруги на одноомному резисторі, еквівалентний опір становить 0,999999\(\Omega \), що недостатньо відрізняється, щоб змінити ситуацію. Але якби ми спробували використовувати той самий вольтметр для вимірювання падіння напруги на\(2-M\Omega \) резисторі, ми б зменшували опір цієї частини ланцюга в три рази, що призведе до різкої зміни в поведінці всієї схеми. |
Це причина, чому ви не можете використовувати вольтметр для вимірювання різниці напруги між двома різними точками в повітрі або між кінцями шматка дерева. Це аж ніяк не дурна річ, яку хочеться робити, оскільки навколишній світ не є середовищем постійної напруги, найекстремальнішим прикладом є те, коли назріває електрична буря. Але зі звичайним вольтметром це не вийде, оскільки опір повітря або деревини багато гігаом. Ефект розмахування пари зондів вольтметра навколо в повітрі полягає в тому, що ми забезпечуємо шлях возз'єднання позитивних і негативних зарядів, які були розділені - через сам вольтметр, який є хорошим провідником порівняно з повітрям. Це зводить до нуля різницю напруги, яку ми намагалися виміряти.
Взагалі, вольтметр, який був встановлений з розімкнутою ланцюгом (або дуже великим опором) між його щупами, як кажуть, «плаваючий». Старомодний аналоговий вольтметр описаного тут типу буде зчитувати нуль при залишеному плаваючому, такий же, як коли він сидів на полиці. Плаваючий цифровий вольтметр зазвичай показує повідомлення про помилку.
9.2.3 Серійні опори

ч/1. Акумулятор проганяє струм через два резистори послідовно. Є три області постійної напруги. Три відмінності напруги пов'язані між собою. Якщо лічильник краб-ходить по ланцюгу, не перегортаючи і не перетинаючи ноги, отримані напруги мають знаки плюс і мінус, які змушують їх складати до нуля.
Дві основні схеми схеми паралельні та послідовні, тому пара резисторів послідовно, h /1, є ще однією з найосновніших схем, які ми можемо зробити. За збереженням заряду весь струм, який протікає через один резистор, також повинен протікати через інший (як і через батарею):
Єдиний спосіб, яким буде корисна інформація про два значення опору, - це якщо ми можемо застосувати закон Ома, який буде співвідносити опір кожного резистора з струмом, що протікає через нього, і різницею напруги на ньому. На малюнку h /2 показані три області постійної напруги. Різниця напруг є більш фізично значними, ніж напруги, тому ми визначаємо символи відмінностей напруги на двох резисторах на малюнку h /3.
У нас є три області постійної напруги, з символами різниці напруги між кожною можливою парою з них. Ці три перепади напруги повинні бути пов'язані один з одним. Це так, ніби я кажу вам, що Фред на ногу вище, ніж Імбир, Імбир на ногу вище Саллі, а Фред на два фути вище, ніж Саллі. Інформація є надлишковою, і вам дійсно потрібні лише два з трьох частин даних, щоб зробити висновок про третій. У разі наших перепадів напруги ми маємо
Знаки абсолютного значення пов'язані з неоднозначністю того, як ми визначаємо наші відмінності напруги. Якби ми перевернули два щупа вольтметра, то отримаємо результат з протилежним знаком. Цифрові вольтметри фактично забезпечать знак мінуса на екрані, якщо провід, підключений до вилки «V», нижче за напругою, ніж той, що підключений до вилки «СОМ». Аналогові вольтметри притискають голку до кілочка, якщо ви намагаєтеся використовувати їх для вимірювання негативних напруг, тому доведеться возитися, щоб висновки були підключені правильно, а потім самостійно подавати будь-який необхідний знак мінус.
На малюнку h /4 показаний стандартний спосіб догляду за неоднозначністю знаків. Для кожного з трьох вимірювань напруги навколо петлі тримаємо один і той же щуп (темніший) на стороні годинникової стрілки. Це так, ніби вольтметр сидів навколо ланцюга, як краб, ніколи не «перетинаючи ноги». З цією умовністю взаємозв'язок між перепадами напруги стає
або, в більш симетричній формі,
Більш загально, це відоме як правило циклу для аналізу схем:
Припускаючи стандартну угоду для знаків плюс і мінус, сума падінь напруги навколо будь-якого замкнутого контуру в ланцюзі повинна дорівнювати нулю.
Шукаючи виняток із правила циклу, було б як просити похід, який би був вниз весь шлях, і що повернеться до своєї відправної точки!
Для схеми, яку ми поставили для аналізу, рівняння
тепер можна переписати, застосовуючи закон Ома до кожного резистора:
Струми однакові, тому ми можемо врахувати їх:
і це той самий результат, який ми б отримали, якби ми аналізували ланцюг з одним резистором з опором\(R_1+R_2\). При цьому еквівалентний опір резисторів послідовно дорівнює сумі їх опорів.
| Приклад 15: Дві лампочки послідовно |
|---|
| \(\triangleright\)Якщо дві однакові лампочки розміщені послідовно, як їх яскравість порівняти з яскравістю однієї лампочки?
i/Приклад 15.
\(\triangleright\)Взяті в цілому, пара лампочок діють як подвоєний опір, тому вони будуть тягнути в два рази менше струму від стіни. Кожна лампочка буде тьмянішою, ніж була б одна лампочка. Загальна потужність, що розсіюється ланцюгом, становить\(I\Delta V\). Падіння напруги по всій схемі таке ж, як і раніше, але струм зменшується вдвічі, тому схема з двома лампочками отримує вдвічі менше загальної потужності, ніж схема з однією лампочкою. Кожна лампочка витягує одну чверть від нормальної потужності. Грубо кажучи, ми могли б очікувати, що це призведе до однієї чверті світла, що виробляється кожною лампочкою, але насправді лампочки витрачають досить високий відсоток своєї потужності у вигляді тепла та довжин хвиль світла, які не видно (інфрачервоні та ультрафіолетові). Менше світла буде вироблятися, але складно передбачити точно, наскільки менше, так як ККД лампочок буде змінюватися при експлуатації їх в різних умовах. |
| Приклад 16: Більше двох рівних опорів послідовно |
|---|
| Шляхом простого застосування методики поділя-володарюй, розглянутої в попередньому розділі, ми виявляємо, що еквівалентний опір\(N\)\(R\) однакових опорів послідовно буде\(NR\). |
| Приклад 17: Залежність опору від довжини |
|---|
| У попередньому розділі ми довели, що опір обернено пропорційно площі поперечного перерізу. За еквівалентною причиною щодо опорів послідовно ми виявляємо, що опір пропорційний довжині. Аналогічно продувати через довгу соломинку важче, ніж через коротку.
j/Подвоєння довжини резистора - це як поставити два резистори послідовно. Опір подвоюється. |
Склавши два аргументи разом, ми виявимо, що опір предмета з прямими, паралельними сторонами задається
Константа пропорційності називається питомим опором, і залежить воно тільки від речовини, з якого зроблений об'єкт. Вимірювання питомого опору може бути використано, наприклад, для ідентифікації зразка невідомої речовини.
| Приклад 18: Вибір високої напруги для ліній електропередач |
|---|
| Томас Едісон вплутався в відому технологічну суперечку з приводу різниці напруг, яку слід використовувати для ліній електропередач. В цей час громадськість була незнайома з електрикою, і легко його лякала. Наприклад, президент Сполучених Штатів відмовився мати електричне освітлення в Білому домі, коли воно вперше стало комерційно доступним, оскільки вважав це небезпечним, віддаючи перевагу відомій пожежонебезпеці масляних ламп таємничій небезпеці електрики. Головним чином як спосіб подолати суспільний страх, Едісон вважав, що потужність повинна передаватися за допомогою малих напруг, і він оприлюднив свою думку, даючи демонстрації, на яких собаку заманювали в положення, щоб бути вбитим великою різницею напруги між двома листами металу на землі. (Противники Едісона також виступали за змінний струм, а не постійний струм, а змінний струм небезпечніше, ніж постійний струм. Як ми обговоримо пізніше, змінний струм можна легко збільшити і опустити до потрібного рівня напруги за допомогою пристрою, званого трансформатором.) Тепер, якщо ми хочемо доставити певну кількість енергії\(P_L\) до навантаження, наприклад електричної лампочки, ми обмежені лише рівнянням\(P_{L} = I\Delta V_L\). Ми можемо поставити будь-яку кількість енергії, яку ми бажаємо, навіть при низькій напрузі, якщо ми готові використовувати великі струми. Сучасні електричні розподільні мережі, однак, використовують небезпечно високі перепади напруги в десятки тисяч вольт. Чому Едісон програв дебати? Це зводиться до грошей. Електрична компанія повинна доставляти\(P_L\) бажану замовником кількість енергії через лінію електропередачі, опір якої\(R_T\) фіксується економікою та географією. Один і той же струм протікає як через навантаження, так і по лінії електропередачі, з користю розсіюючи потужність в першій і марно в другій. Ефективність системи становить \[\begin{align*} \text{efficiency} &= \frac{\text{power paid for by the customer}} {\text{power paid for by the utility}} \\ &= \frac{ P_{L}}{ P_L+ P_{T}} \\ &= \frac{1}{1+ P_{T}/ P_L} \end{align*}\] Поставивши себе на місце електричної компанії, ми хочемо позбутися змінної\(P_T\), оскільки це те, що ми контролюємо лише опосередковано своїм вибором\(\Delta V_T\) і\(I\). Підставляючи\(P_{T}= I\Delta V_T\), знаходимо \[\begin{equation*} \text{efficiency} = \frac{1} {1+\frac{ I \Delta V_T}{ P_L}} \end{equation*}\] Припускаємо, що лінія електропередачі (але не обов'язково навантаження) омічна, тому підстановка\(\Delta V_T=IR_T\) дає \[\begin{equation*} efficiency = \frac{1}{1+\frac{I^2R_T}{P_L}} \end{equation*}\] Цю величину можна чітко збільшити, зробивши\(I\) якомога менше, оскільки ми будемо ділити на найменшу можливу кількість на дні фракції. Низькострумова ланцюг може забезпечити значну кількість енергії лише в тому випадку, якщо вона використовує високі напруги, саме тому системи електричної передачі використовують небезпечні високі напруги. |
| Приклад 19: Вбиття амперметром |
|---|
| Як і у випадку з вольтметром, амперметр може давати помилкові показання, якщо його використовувати таким чином, що він змінює поведінку ланцюга. Амперметр використовується послідовно, тому якщо він використовується для вимірювання струму через резистор, значення резистора буде ефективно змінено на\(R+ R_a\), де\(R_a\) знаходиться опір амперметра. Амперметри розроблені з дуже низькими опорами для того, щоб зробити малоймовірним, що\(R+ R_a\) буде істотно відрізнятися від\(R\). Насправді справжньою небезпекою є смерть, а не неправильне читання! Практично єдині ланцюги, опір яких значно менше, ніж у амперметра, - це ті, які призначені для перенесення величезних струмів. Амперметр, вставлений в такий контур, може легко розплавитися. Коли я працював у лабораторії, що фінансується Міністерством енергетики, ми отримували періодичні бюлетені з офісу безпеки DOE про серйозні аварії на інших об'єктах, і вони мали певне огидне захоплення. Один з них стосувався працівника DOE, який був повністю спалений вибухом, створеним, коли він вставив звичайний амперметр Radio Shack у високострумовий ланцюг. Пізніші оцінки показали, що тепло, ймовірно, було настільки інтенсивним, що вибух був кулькою плазми - газу настільки гарячого, що його атоми були іонізовані. |

k/Приклад 20.
| Приклад 20: Складна схема |
|---|
| \(\triangleright\)Всі сім резисторів на лівій панелі малюнка k ідентичні. Спочатку вимикач S розімкнутий, як показано на малюнку, а струм через резистор А -\(I_\text{o}\). Потім вимикач закривається. Знайти струм через резистор B, після замикання вимикача, в перерахунку\(I_\text{o}\). \(\triangleright\)Друга панель показує схему, перемальовану для простоти, в початковому стані з розімкнутим вимикачем. Коли вимикач відкритий, жоден струм не може протікати через центральний резистор, тому ми можемо також ігнорувати його. Я також перемалював з'єднання, не змінюючи те, що пов'язано з чим. Це свого роду розумова перестановка, яку ви в кінцевому підсумку навчитеся робити автоматично з досвіду аналізу схем. Перемальована версія полегшує перегляд того, що відбувається з поточною. Заряд зберігається, тому будь-який заряд, який протікає повз точки 1 в ланцюзі, також повинен протікати повз точок 2 і 3. Це було б важче міркувати, застосувавши правило з'єднання до оригінальної версії, яка, здається, має дев'ять окремих з'єднань. У новій версії також зрозуміло, що схема має велику симетрію. Ми могли б перевернути кожну паралельну пару однакових резисторів, не змінюючи те, що підключено до чого, так що дає зрозуміти, що падіння напруги та струми повинні бути рівними для членів кожної пари. Ми також можемо довести це за допомогою правила циклу. Правило петлі говорить, що два падіння напруги в контурі 4 повинні бути рівними, причому аналогічно для петель 5 і 6. Оскільки резистори підкоряються закону Ома, рівні перепади напруги на них також мають на увазі рівні струми. Це означає, що коли струм в точці 1 доходить до верхнього переходу, рівно половина його проходить через кожен резистор. Потім струм возз'єднується на 2, розщеплюється між наступною парою і так далі. Робимо висновок, що кожен з шести резисторів в схемі відчуває однакове падіння напруги і однаковий струм. Застосовуючи правило петлі до циклу 7, ми виявляємо, що сума трьох падінь напруги на трьох лівих резисторах дорівнює напрузі акумулятора\(V\), тому кожен резистор в ланцюзі відчуває падіння напруги\(V/3\). Даючи\(R\) стояти за опір одного з резисторів, виявляємо, що струм через резистор В, який такий же, як і струми через всі інші, задається\(I_\text{o}=V/3R\). Тепер переходимо до корпусу, де вимикач закритий, як показано на третій панелі. Напруга акумулятора таке ж, як і раніше, і опір кожного резистора однаковий, тому ми все ще можемо використовувати ті ж символи\(V\) і\(R\) для них. Однак більше не вірно, що кожен резистор відчуває падіння напруги\(V/3\). Еквівалентне опір всієї ланцюга є\(R/2+R/3+R/2=4R/3\), тому сумарний струм, що відводиться від акумулятора, дорівнює\(3V/4R\). У середній групі резисторів цей струм розщеплюється трьома способами, тому новий струм через В є\((1/3)(3V/4R)=V/4R=3I_\text{o}/4\). Інтерпретуючи цей результат, ми бачимо, що він походить від двох ефектів, які частково скасовують. Замикання вимикача зменшує еквівалентний опір ланцюга, даючи заряду іншим способом протікання, і збільшує величину струму, що відводиться від акумулятора. Резистор B, однак, отримує лише 1/3 частку цього більшого струму, а не 1/2. Другий ефект виявляється більше першого, а тому струм через резистор В зменшується по всьому. |
Обговорення Питання
◊ Ми виклали правило петлі в симетричній формі, де ряд падінь напруги додає до нуля. Для цього нам довелося визначити стандартний спосіб підключення вольтметра до схеми, щоб знаки «плюс» і «мінус» виходили правильно. Припустимо, ми хочемо перевстановити правило з'єднання аналогічним симетричним способом, щоб замість того, щоб прирівняти струм, що надходить до струму, що виходить, він просто стверджує, що певна сума струмів на стику додає до нуля. Який стандартний спосіб вставки амперметра нам довелося б використовувати, щоб зробити цю роботу?
Дописувачі