2.1: Маса

Last updated
Save as PDF

Page ID: 73446

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Зміни неможливі, стверджував давньогрецький філософ Парменід. Його робота була ненауковою, оскільки він не висловлював свої ідеї у формі, яка дозволила б їх випробувати експериментальним шляхом, але сучасна наука все ж має сильний парменідеанський аромат. Його головний аргумент про те, що зміни є ілюзією, полягав у тому, що щось не можна перетворити ні на що, і так само, якщо у вас нічого немає, ви не можете перетворити це на щось. Щоб перетворити це в наукову теорію, ми повинні вирішити, як виміряти, що таке «щось», і тоді ми можемо перевірити за допомогою вимірювань, чи загальна кількість «чогось» у Всесвіті дійсно залишається постійною. Скільки «чогось» є в скелі? Чи вважається сонячний промінь «чимось?» Чи враховується тепло? Рух? Думки і почуття.

Якщо ви подивитеся на зміст цієї книги, то побачите, що перші чотири глави мають в них слово «збереження». У фізиці закон збереження - це твердження про те, що загальна кількість певної фізичної величини завжди залишається однаковою. У цій главі йдеться про збереження маси. Метрична система розроблена навколо одиниці відстані, метра, одиниці маси, кілограма та одиниці часу, друга. Чисельне вимірювання відстані та часу, ймовірно, датується майже настільки ж далекою передісторією, як підрахунок грошей, але маса - це більш сучасна концепція. Поки вчені не з'ясували, що маса збережена, не було очевидно, що може існувати єдиний послідовний спосіб вимірювання кількості речовини, отже, джигери віскі та шнури дерева. Ви можете здивуватися, чому збереження маси не було виявлено до відносно нового часу, але це не було очевидно, наприклад, що гази мають масу, і що очевидна втрата маси при спалюванні деревини точно відповідає масі газів, що випливають.

Після того, як вчені були на шляху збереження концепції маси, вони почали шукати спосіб визначення маси з точки зору певної вимірювальної процедури. Якби спробували таку процедуру, і в результаті вийшло, що вона призвела до неконсервації маси, то викинули б її і спробували іншу процедуру. Наприклад, у нас може виникнути спокуса визначити масу за допомогою кухонних мірних чашок, тобто як міра об'єму. Потім маса буде ідеально законсервована для такого процесу, як змішування мармуру з арахісовим маслом, але були б такі процеси, як заморожування води, що призвело до чистого збільшення маси, та інші, як замочування води губкою, що спричинило зменшення. Якщо, з користю заднього огляду, здається, що визначення мірної чашки було просто нерозумно, то ось більш тонкий приклад неправильного визначення маси. Припустимо, ми визначаємо його за допомогою ваги для ванної кімнати або більш точного пристрою, такого як поштова шкала, яка працює за тим же принципом використання сили тяжіння для стиснення або скручування пружини. Біда полягає в тому, що гравітація не однаково сильна по всій поверхні землі, тому, наприклад, було б незбереження маси, коли ви піднесете об'єкт на вершину гори, де гравітація трохи слабша.

Хоча деякі очевидні можливості мають проблеми, виявляється, принаймні, два підходи до визначення маси, які призводять до того, що вона є збереженою кількістю, тому ми вважаємо ці визначення «правильними» в прагматичному сенсі, що те, що правильно, - це те, що корисно.

Одне визначення, яке працює, - використовувати баланси, але компенсувати місцеву силу тяжіння. Це метод, який використовують вчені, які насправді спеціалізуються на надточних вимірах. Стандартний кілограм, у вигляді платиново-іридієвого циліндра, зберігається в спеціальній святині в Парижі. Робляться копії, які балансують проти стандартного кілограма в паризькій гравітації, а потім вони транспортуються в лабораторії в інших куточках світу, де їх порівнюють з іншими масами в місцевій гравітації. Визначена таким чином величина називається гравітаційною масою.

Малюнок б: Вимірювання гравітаційної маси: сфера має гравітаційну масу п'ять кілограмів.

Другий і зовсім інший підхід полягає в тому, щоб виміряти, наскільки важко змінити стан руху об'єкта. Це говорить нам про його інерційній масі. Наприклад, я б охочіше стояв на шляху зустрічного пуделя, ніж на шляху вантажного поїзда, тому що моєму тілу буде важче переконати вантажний потяг зупинитися. Це концептуальне визначення у словниковому стилі, але у фізиці нам потрібно створити резервну копію концептуального визначення операційним визначенням, яке описує операції, необхідні для вимірювання визначеної кількості. Ми можемо операціоналізувати наше визначення інерційної маси, кинувши стандартний кілограм на об'єкт зі швидкістю 1 м/с (один метр в секунду) і виміряючи швидкість відкатного об'єкта. Припустимо, ми хочемо виміряти масу конкретного блоку цементу. Ставимо блок в іграшковий візок на тротуарі, і скидаємо на нього стандартний кілограм. Припустимо, стандартний кілограм б'є в вагон, а потім опускається прямо вниз на тротуар, втративши всю свою швидкість, а вагон і блок всередині віддачі зі швидкістю 0,23 м/с Потім повторюємо експеримент з блоком, заміненим різною кількістю стандартних кілограмів, і знаходимо, що можемо відтворювати швидкість віддачі 0,23 м/с при чотирьох стандартних кілограмах у вагоні. Ми визначили масу блоку в чотири кілограми. ¹ Хоча це визначення інерційної маси має привабливу концептуальну простоту, воно, очевидно, не дуже практичне, принаймні в цій грубій формі. Проте цей метод зіткнення дуже схожий на методи вимірювання мас субатомних частинок, які, врешті-решт, не можна поставити на маленькі поштові ваги!

Малюнок в: Вимірювання інерційної маси: вагон відкачується з однаковою швидкістю в дослідах 1 і 2, встановлюючи, що інерційна маса цементного блоку дорівнює чотирьом кілограмам.

Космонавтам, які проводять тривалі періоди часу в космосі, необхідно стежити за втратою кісткової і м'язової маси, а тут також неможливо виміряти гравітаційну масу. Оскільки вони не хочуть, щоб на них кидали стандартні кілограми, вони використовують дещо іншу техніку (цифри d і e). Вони прив'язуються до стільця, який кріпиться до великої пружини, і вимірюють час, необхідний для одного циклу вібрації.

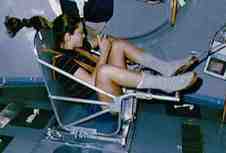
Малюнок d (зліва): Час одного циклу вібрації пов'язане з інерційною масою об'єкта.

Малюнок е (праворуч): Астронавт Тамара Джерніган вимірює свою інерційну масу на борту космічного човника.

1.1.1 Методи вирішення проблем

Як ми використовуємо закон збереження, такий як збереження маси, для вирішення проблем? Існує дві основні методики.

Як аналогію розгляньте збереження грошей, що робить незаконним для вас створення доларових купюр за допомогою власного струменевого принтера. (Більшість людей не навмисно знищують свої доларові купюри, або!) Припустимо, поліція помічає, що конкретний магазин, здається, не має клієнтів, але власник носить багато золотих прикрас і їздить на BMW. Вони підозрюють, що магазин - це фронт для якогось злочину, можливо, підробки. При інтенсивному спостереженні існує два основних підходи, які вони могли б використовувати в своєму розслідуванні. Одним із методів було б мати агентів під прикриттям спробувати з'ясувати, скільки грошей йде у двері, і скільки грошей повертається наприкінці дня, можливо, домовляючись через якийсь трюк, щоб отримати доступ до портфеля власника вранці та ввечері. Якщо сума грошей, яка виходить щодня, перевищує суму, яка надійшла, і якщо вони переконані, що немає сейфа в приміщенні, що тримає великий резервуар грошей, то власник повинен бути підробкою. Ця техніка припливу рівних відтоку корисна, якщо ми впевнені, що існує область простору, всередині якої немає запасу маси, яка накопичується або виснажується.

Приклад 1: Потік води
Якщо ви спостерігаєте за тим, як вода витікає з кінця шланга, ви побачите, що потік води товстіший біля гирла шланга, а худий нижче. Це пояснюється тим, що вода прискорюється, коли вона падає. Якби площа поперечного перерізу потоку була рівною по всій його довжині, то швидкість потоку (кілограм в секунду) через менший перетин була б більше, ніж швидкість потоку через поперечний переріз вище вгору. Оскільки потік стабільний, кількість води між двома перетинами залишається постійним. Збереження маси, отже, вимагає, щоб площа поперечного перерізу потоку скорочувалася в зворотній пропорції зростаючої швидкості падаючої води. f/Приклад 1.

Приклад 1: Потік води

Якщо ви спостерігаєте за тим, як вода витікає з кінця шланга, ви побачите, що потік води товстіший біля гирла шланга, а худий нижче. Це пояснюється тим, що вода прискорюється, коли вона падає. Якби площа поперечного перерізу потоку була рівною по всій його довжині, то швидкість потоку (кілограм в секунду) через менший перетин була б більше, ніж швидкість потоку через поперечний переріз вище вгору. Оскільки потік стабільний, кількість води між двома перетинами залишається постійним. Збереження маси, отже, вимагає, щоб площа поперечного перерізу потоку скорочувалася в зворотній пропорції зростаючої швидкості падаючої води.

f/Приклад 1.

самостійна перевірка:

Припустимо, ви спрямовуєте шланг прямо вгору, так що вода піднімається, а не падає. Що відбувається, коли швидкість стає меншою? Що відбувається, коли швидкість стає нульовою?

(відповідь у зворотному боці PDF-версії книги)

Як ми можемо застосувати закон збереження, такий як збереження маси, в ситуації, коли маса може десь зберігатися? Щоб знову використати аналогію зі злочинністю, в'язниця може містити певну кількість ув'язнених, яким заборонено текти або виходити за власним бажанням. У фізиці це відомо як замкнута система. Охоронець може помітити, що певна камера в'язня порожня, але це не означає, що він втік. Він міг захворіти в лазареті, або наполегливо працювати в магазині, заробляючи сигаретні гроші. Те, що в'язниці насправді роблять, це підраховувати всіх своїх ув'язнених щодня, і переконатися, що сьогоднішня загальна сума така ж, як і вчорашній. Один із способів заявити про закон збереження полягає в тому, що для закритої системи загальна кількість матеріалу (маса, у цій главі) залишається постійною.

Приклад 2: Лавуазьє і хімічні реакції в закритій системі
Французький хімік Антуан Лоран Лавуазьє вважається винахідником концепції збереження маси. До Лавуазьє хіміки ніколи систематично не зважували свої хімічні речовини, щоб кількісно оцінити кількість кожної речовини, яка зазнала реакції. Вони також не повністю розуміли, що гази - це просто інший стан речовини, і не намагалися виконувати реакції в герметичних камерах, щоб визначити, чи споживаються гази з повітря або вивільняються в нього. Для цього у них було хоча б одне практичне виправдання, яке полягає в тому, що якщо ви виконуєте реакцію газовиділення в герметичній камері без місця для розширення, ви отримаєте вибух! Лавуазьє винайшов баланс, здатний вимірювати міліграмові маси, і придумав, як робити реакції в перевернутій чаші в басейні з водою, щоб гази могли розширюватися, виштовхуючи частину води. У вирішальному експерименті Лавуазьє нагрів червону сполуку ртуті, яку ми зараз описали як оксид ртуті (HgO), в такій герметичній камері. Був вироблений газ (пізніше Лавуазьє назвав його «кисень»), витісняючи частину води, а червоне з'єднання перетворилося на сріблястий рідкий ртутний метал. Найважливішим моментом було те, що загальна маса всього апарату була абсолютно однаковою до і після реакції. Виходячи з багатьох спостережень цього типу, Лавуазьє запропонував загальний закон природи, що маса завжди зберігається. (У попередніх експериментах, в яких замкнуті системи не використовувалися, хіміки переконалися, що в реакціях горіння і окислення бере участь загадкове речовина - флогистон, і що маса флогистона може бути позитивною, негативною або нульовою залежно від ситуації!) a/Портрет месьє Лавуазьє і його дружини, автор Жак-Луї Давид, 1788. Лавуазьє винайшов концепцію збереження маси. Чоловік зображений зі своїм науковим апаратом, а на задньому плані зліва - портфоліо, що належить мадам Лавуазьє, яка, як вважають, була студенткою Девіда.

Приклад 2: Лавуазьє і хімічні реакції в закритій системі

Французький хімік Антуан Лоран Лавуазьє вважається винахідником концепції збереження маси. До Лавуазьє хіміки ніколи систематично не зважували свої хімічні речовини, щоб кількісно оцінити кількість кожної речовини, яка зазнала реакції. Вони також не повністю розуміли, що гази - це просто інший стан речовини, і не намагалися виконувати реакції в герметичних камерах, щоб визначити, чи споживаються гази з повітря або вивільняються в нього. Для цього у них було хоча б одне практичне виправдання, яке полягає в тому, що якщо ви виконуєте реакцію газовиділення в герметичній камері без місця для розширення, ви отримаєте вибух! Лавуазьє винайшов баланс, здатний вимірювати міліграмові маси, і придумав, як робити реакції в перевернутій чаші в басейні з водою, щоб гази могли розширюватися, виштовхуючи частину води. У вирішальному експерименті Лавуазьє нагрів червону сполуку ртуті, яку ми зараз описали як оксид ртуті (HgO), в такій герметичній камері. Був вироблений газ (пізніше Лавуазьє назвав його «кисень»), витісняючи частину води, а червоне з'єднання перетворилося на сріблястий рідкий ртутний метал. Найважливішим моментом було те, що загальна маса всього апарату була абсолютно однаковою до і після реакції. Виходячи з багатьох спостережень цього типу, Лавуазьє запропонував загальний закон природи, що маса завжди зберігається. (У попередніх експериментах, в яких замкнуті системи не використовувалися, хіміки переконалися, що в реакціях горіння і окислення бере участь загадкове речовина - флогистон, і що маса флогистона може бути позитивною, негативною або нульовою залежно від ситуації!)

a/Портрет месьє Лавуазьє і його дружини, автор Жак-Луї Давид, 1788. Лавуазьє винайшов концепцію збереження маси. Чоловік зображений зі своїм науковим апаратом, а на задньому плані зліва - портфоліо, що належить мадам Лавуазьє, яка, як вважають, була студенткою Девіда.

1.1.2 Дельта позначення

Зручним позначенням, використовуваним у всій фізиці$\Delta$, є велика грецька буква дельта, яка вказує на «зміна» або «після мінус перед». Наприклад, якщо$b$ представляє, скільки грошей у вас є в банку, то депозит у розмірі 100 доларів можна представити як $\ Delta {} b=$100$. Тобто зміна вашого балансу склало 100 доларів, або залишок після операції мінус залишок до транзакції дорівнює 100$. Відкликання буде вказано$\Delta{}b\lt0$. Ми представляємо «до» та «після», використовуючи індекси$i$ (початкові) та$f$ (кінцеві), наприклад,$\Delta{}b=b_f-b_i$. Часто дельта-позначення допускає більшу точність, ніж англійські слова. Наприклад, «час» може бути використаний як момент часу («зараз час»)$t$, або це може означати проміжок часу («весь час, він плював на підборідді»),$\Delta{}t$.

Це позначення особливо зручно для обговорення законсервованих кількостей. Закон збереження маси можна констатувати просто так$\Delta{}m=0$, де$m$ знаходиться загальна маса будь-якої замкнутої системи.

самостійна перевірка:

Якщо$x$ представляє розташування об'єкта, що рухається в одному вимірі, то як$\Delta{}x$ будуть інтерпретовані позитивні та негативні ознаки?

(відповідь у зворотному боці PDF-версії книги)

Питання для обговорення

If an object had a straight-line $x-t$ graph with $\Delta x=0$ and $\Delta t\ne0$, what would be true about its velocity? What would this look like on a graph? What about $\Delta t=0$ and $\Delta x\ne0$?

Contributors and Attributions

Template:ContribCrowell