22.2: Гіроскоп
- Page ID
- 75739
Іграшковий гіроскоп маси\(m\) складається з обертового маховика, встановленого в рамці підвіски, що дозволяє осі маховика вказувати в будь-якому напрямку. Один кінець осі спирається на пілон\(a\) відстані\(d\) від центру маси гіроскопа.

Вибирайте полярні координати так, щоб вісь маховика гіроскопа була вирівняна по осі r, а вертикальна вісь - вісь z (на малюнку 22.2 показано схематичне зображення гіроскопа).
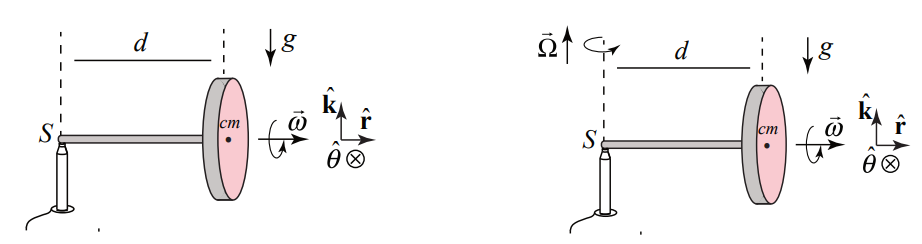
Маховик обертається навколо своєї осі з кутовою швидкістю обертання,
\[\overrightarrow{\boldsymbol{\omega}}_{s}=\omega_{s} \hat{\mathbf{r}} \nonumber \]
де\(\omega_{s}\) радіальна складова і\(\omega_{s}>0\) для випадку, проілюстрованого на малюнку 22.2.
Коли ми випускаємо гіроскоп, він зазнає дуже дивного руху. Замість того, щоб падати вниз, центр мас обертається навколо вертикальної осі, яка проходить через точку\(S\) контакту осі з пілоном з прецесійною кутовою швидкістю
\[\overrightarrow{\boldsymbol{\Omega}}=\Omega_{z} \hat{\mathbf{k}}=\frac{d \theta}{d t} \hat{\mathbf{k}} \nonumber \]
де\(\Omega_{z}=d \theta / d t\) z -компонент і\(\Omega_{z}>0\) для випадку, проілюстрованого на малюнку 22.3. Тому кутова швидкість маховика - це сума цих двох внесків.
\[\overrightarrow{\boldsymbol{\omega}}=\overrightarrow{\boldsymbol{\omega}}_{s}+\overrightarrow{\boldsymbol{\Omega}}=\omega_{s} \hat{\mathbf{r}}+\Omega_{z} \hat{\mathbf{k}} \nonumber \]
Вивчимо окремий випадок, коли величина\(\left|\Omega_{z}\right|\) прецесійної складової кутової швидкості набагато менше величини спінової\(\left|\omega_{s}\right|\) складової кутової швидкості\(\left|\Omega_{z}\right|<<\mid \omega_{s}\), так що величина кутової швидкості\(|\vec{\omega}| \simeq\left|\omega_{\mathrm{s}}\right| \text { and } \Omega_{z} \text { and } \omega_{s}\) майже постійна. Ці припущення в сукупності називаються гіроскопічним наближенням.
Діаграма сил для гіроскопа показана на малюнку 22.4. Гравітаційна сила діє в центрі маси і спрямована вниз,\(\overrightarrow{\mathbf{F}}^{g}=-m g \hat{\mathbf{k}}\). Існує також контактна сила,\(\overrightarrow{\mathbf{F}}^{c}\) між кінцем осі і пілоном. Може здатися, що контактна сила\(\overrightarrow{\mathbf{F}}^{c}\) має лише висхідну складову\(\overrightarrow{\mathbf{F}}^{v}=F_{z} \hat{\mathbf{k}}\), але, як ми незабаром побачимо, також повинна бути радіальна внутрішня складова контактної сили,\(\overrightarrow{\mathbf{F}}^{r}=F_{r} \hat{\mathbf{r}}, \text { with } F_{r}<0\) оскільки центр маси зазнає кругового руху.
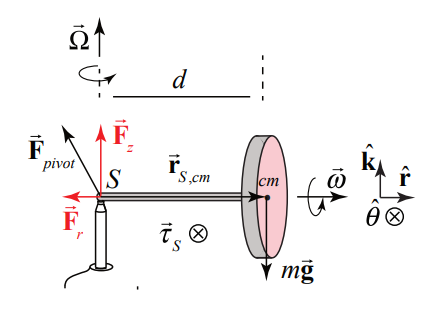
Причина того, що гіроскоп не падає вниз, полягає в тому, що вертикальна складова контактної сили точно врівноважує силу тяжіння.
\[F_{z}-m g=0 \nonumber \]
Як щодо крутного моменту щодо точки контакту\(S\)? Контактна сила діє при\(S\) тому, що вона не сприяє крутному моменту близько\(S\); тільки гравітаційна сила сприяє крутному моменту близько\(S\) (рис. 22.5b). Напрямок крутного моменту про\(S\) задається
\[\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, \mathrm{cm}} \times \overrightarrow{\mathbf{F}}_{\mathrm{gravity}}=d \hat{\mathbf{r}} \times m g(-\hat{\mathbf{k}})=d m g \hat{\boldsymbol{\theta}} \nonumber \]
і знаходиться в\(\hat{\boldsymbol{\theta}}\) позитивному напрямку. Однак ми знаємо, що якщо є ненульовий крутний момент близько\(S\), то кутовий момент близько\(S\) повинен змінюватися в часі, згідно
\[\vec{\tau}_{S}=\frac{d \overrightarrow{\mathrm{L}}_{S}}{d t} \nonumber \]
Кутовий момент про точку\(S\) гіроскопа задається
\[\overrightarrow{\mathbf{L}}_{S}=\overrightarrow{\mathbf{L}}_{S}^{\text {otbital }}+\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\text {spin }} \nonumber \]
Орбітальний момент моменту навколо точки\(S\) дорівнює
\[\overrightarrow{\mathbf{L}}_{S}^{\text {otbial }}=\overrightarrow{\mathbf{r}}_{S, c m} \times m \overrightarrow{\mathbf{v}}_{c m}=d \hat{\mathbf{r}} \times m d \Omega_{z} \hat{\boldsymbol{\theta}}=m d^{2} \Omega_{z} \hat{\mathbf{k}} \nonumber \]
Величина орбітального моменту\(S\) близько майже постійна і напрямок не змінюється. Тому
\[\frac{d}{d t} \overrightarrow{\mathbf{L}}_{S}^{\text {obital }}=\overrightarrow{\mathbf{0}} \nonumber \]
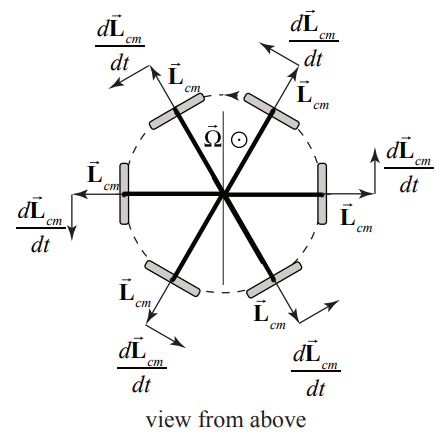
Кутовий імпульс обертання включає два терміни. Нагадаємо, що маховик зазнає два окремих обертання навколо різних осей. Він обертається навколо осі маховика з кутовою швидкістю обертання\(\overrightarrow{\boldsymbol{\omega}}_{s}\). У міру попередження маховика навколо точки повороту маховик обертається навколо осі z з прецесійною кутовою швидкістю\(\overrightarrow{\mathbf{\Omega}}\) (рис. 22.5). Таким чином, кутовий імпульс обертання задається
\[\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\operatorname{spin}}=I_{r} \omega_{s} \hat{\mathbf{r}}+I_{z} \Omega_{z} \hat{\mathbf{k}} \nonumber \]
де\(I_{r}\) - момент інерції щодо осі маховика і\(I_{z}\) - момент інерції щодо осі z. Якщо припустити, що вісь безмасова і маховик рівномірний з радіусом R, то\(I_{r}=(1 / 2) m R^{2}\). За перпендикулярною віссю теорема\(I_{r}=I_{z}+I_{y}=2 I_{z}\) звідси\(I_{z}=(1 / 4) m R^{2}\).

Нагадаємо, що гіроскопічне наближення тримає, коли,\(\left|\Omega_{z}\right|<<\left|\omega_{s}\right|\) що означає, що\(I_{z} \Omega_{z}<<I_{r} \omega_{s}\) і тому ми можемо ігнорувати внесок у спіновий кутовий імпульс від обертання навколо вертикальної осі, і так
\[\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\operatorname{spin}} \simeq I_{\mathrm{cm}} \omega_{s} \hat{\mathbf{r}} \nonumber \]
(Внесок у спіновий момент, обумовлений обертанням навколо осі z,\(I_{z} \Omega_{z} \hat{\mathbf{k}}\) майже постійний як за величиною, так і за напрямком, тому він не змінюється в часі,\(d\left(I_{z} \Omega_{z} \hat{\mathbf{k}}\right) / d t \simeq \overrightarrow{\mathbf{0}}\). Тому момент імпульсу приблизно\(S\) дорівнює.
\[\overrightarrow{\mathbf{L}}_{S} \simeq \overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\mathrm{spin}}=I_{\mathrm{cm}} \omega_{s} \hat{\mathbf{r}} \nonumber \]
Наше початкове очікування того, що гіроскоп повинен впасти вниз через крутного моменту, який сила тяжіння чинить щодо точки контакту,\(S\) призводить до порушення закону крутного моменту. Якщо центр маси дійсно почав падати, то зміна кута обертання, вказуватиме на негативний z -напрямок,\(\Delta \overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\operatorname{spin}}\) і це суперечило б векторному аспекту рівняння (22.2.6). Замість того, щоб падати вниз, кутовий момент навколо центру маси,\(\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\mathrm{spin}}\) повинен змінити напрямок таким чином, щоб напрямок\(\Delta \overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\text {spin }}\) знаходиться в тому ж напрямку, що і крутний момент про\(S\) (Рівняння (22.2.5)), позитивний\(\hat{\boldsymbol{\theta}}\) -напрямок.
Нагадаємо, що в нашому дослідженні кругового руху ми вже стикалися з декількома прикладами, в яких змінюється напрямок вектора постійної величини. Розглянуто точковий об'єкт маси m, що рухається по колу радіуса r. Коли ми вибираємо систему координат з початком у центрі кола, вектор положення\(\overrightarrow{\mathbf{r}}\) спрямований радіально назовні. Коли маса рухається по колу, вектор положення має постійну величину, але змінюється в напрямку. Вектор швидкості задається
\[\overrightarrow{\mathbf{v}}=\frac{d \overrightarrow{\mathbf{r}}}{d t}=\frac{d}{d t}(r \hat{\mathbf{r}})=r \frac{d \theta}{d t} \hat{\boldsymbol{\theta}}=r \omega_{z} \hat{\boldsymbol{\theta}} \nonumber \]
і має напрямок, яке перпендикулярно вектору положення (дотична до кола), (рис. 22.7а)).

Для рівномірного кругового руху величина швидкості постійна, але напрямок постійно змінюється, і ми виявили, що прискорення задається (рис. 22.7b)
\[\overrightarrow{\mathbf{a}}=\frac{d \overrightarrow{\mathbf{v}}}{d t}=\frac{d}{d t}\left(v_{\theta} \hat{\boldsymbol{\theta}}\right)=v_{\theta} \frac{d \theta}{d t}(-\hat{\mathbf{r}})=r \omega_{z} \omega_{z}(-\hat{\mathbf{r}})=-r \omega_{z}^{2} \hat{\mathbf{r}} \nonumber \]
Зауважимо, що ми використовували факти, які
\ [\ почати {масив} {l}
\ frac {d\ hat {\ mathbf {r}} {d t} =\ frac {d\ тета} {d\ тета}\ hat {\ boldsymbol {\ theta}}
\ hat {\ boldsymbol {\ theta}} {d t} =-\ frac {d\ theta} {d\ theta}}\ hat {\ mathbf {r}}
\ кінець {масив}\ nonumber\]
у рівняннях (22.2.13) та (22.2.14). Ми можемо застосувати ті ж міркування до того, як змінюється кутова спина в часі (рис. 22.8).
Похідна часу спінового кутового моменту задається
\[\frac{d \overrightarrow{\mathbf{L}}_{S}}{d t}=\frac{d \overrightarrow{\mathbf{L}}_{\mathrm{cm}, \omega_{s}}^{\operatorname{spin}}}{d t}=\left|\overrightarrow{\mathbf{L}}_{\mathrm{cm}, \omega_{s}}^{\sin }\right| \frac{d \theta}{d t} \hat{\boldsymbol{\theta}}=\left|\overrightarrow{\mathbf{L}}_{\mathrm{cm}, \omega_{s}}^{\sin }\right| \Omega_{z} \hat{\boldsymbol{\theta}}=I_{r} \omega_{s} \Omega_{z} \hat{\boldsymbol{\theta}} \nonumber \]
\(\Omega_{z}=d \theta / d t\)де z -компонент і\(\Omega_{z}>0\). Центр мас маховика обертається навколо вертикальної осі, яка проходить через точку\(S\) контакту осі з пілоном з прецесійною кутовою швидкістю.
\[\overrightarrow{\mathbf{Q}}=\Omega_{z} \hat{\mathbf{k}}=\frac{d \theta}{d t} \hat{\mathbf{k}} \nonumber \]
Замініть рівняння (22.2.16) та (22.2.5) на рівняння (22.2.6), що дають
\[d m g \hat{\boldsymbol{\theta}}=\left|\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\sin }\right| \Omega_{z} \hat{\boldsymbol{\theta}} \nonumber \]
Розв'язування рівняння (22.2.18) для z -складової прецесійної кутової швидкості гіроскопа
\[\Omega_{z}=\frac{d m g}{\left|\overrightarrow{\mathbf{L}}_{\mathrm{cm}}^{\mathrm{spin}}\right|}=\frac{d m g}{I_{\mathrm{cm}} \omega_{\mathrm{s}}} \nonumber \]