14.9: Опрацьовані приклади
- Page ID
- 75698
Приклад 14.2 Швидкість втечі Торо
Астероїд Торо, відкритий в 1964 році, має радіус близько\(R=5.0 \mathrm{km}\) і масу близько\(m_{t}=2.0 \times 10^{15} \mathrm{kg}\). Припустимо, що Торо - це ідеально однорідна сфера. Яка швидкість втечі для об'єкта масою m на поверхні Торо? Чи міг людина досягти цієї швидкості (на землі), бігаючи?
Рішення: Єдиною потенційною енергією в цій задачі є гравітаційна потенційна енергія. Ми вибираємо нульову точку для потенційної енергії, коли об'єкт і Торо знаходяться на нескінченній відстані один від одного,\(U^{G}(\infty) \equiv 0\). При такому виборі потенційна енергія, коли об'єкт і Торо знаходяться на скінченній відстані r один від одного, задається
\[U^{G}(r)=-\frac{G m_{t} m}{r} \nonumber \]
з\(U^{G}(\infty) \equiv 0\) виразом швидкість втечі відноситься до мінімальної швидкості, необхідної об'єкту, щоб уникнути гравітаційної взаємодії астероїда і відійти на нескінченну відстань. Якщо об'єкт має швидкість менше швидкості втечі, він не зможе уникнути сили тяжіння і повинен повернутися до Торо. Якщо об'єкт має швидкість, більшу за швидкість втечі, він матиме ненульову кінетичну енергію на нескінченності. Умовою швидкості втечі є те, що об'єкт матиме рівно нульову кінетичну енергію на нескінченності.
Вибираємо наш початковий стан, в той час\(t_{i}\), коли об'єкт знаходиться на поверхні астероїда зі швидкістю, рівною швидкості втечі. Ми вибираємо наш кінцевий стан, в той час\(t_{f}\), щоб відбуватися, коли відстань поділу між астероїдом і об'єктом нескінченна.
Початкова кінетична енергія є\(K_{i}=(1 / 2) m v_{\mathrm{esc}}^{2}\). Початкова потенційна енергія\(U_{i}=-G m_{t} m / R\) і тому початкова механічна енергія
\[E_{i}=K_{i}+U_{i}=\frac{1}{2} m v_{\mathrm{esc}}^{2}-\frac{G m_{t} m}{R} \nonumber \]
Кінцева кінетична енергія полягає в\(K_{f}=0\) тому, що це c
Умова, що визначає швидкість втечі. Кінцева потенційна енергія дорівнює нулю,\(U_{f}=0\) тому що ми вибрали нульову точку для потенційної енергії на нескінченності. Кінцева механічна енергія тоді
\[E_{f}=K_{f}+U_{f}=0 \nonumber \]
Неконсервативної роботи немає, тому зміна механічної енергії дорівнює нулю
\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]
Тому
\[0=-\left(\frac{1}{2} m v_{\mathrm{esc}}^{2}-\frac{G m_{t} m}{R}\right) \nonumber \]
Це можна вирішити для швидкості втечі,
\ [\ почати {вирівняний}
v_ {\ mathrm {ESC}} &=\ sqrt {\ frac {2 G m_ {t}}\\
&=\ sqrt {\ frac {2\ ліворуч (6.67\ раз 10^ {-11}\ mathrm {N}\ cdot\ mathrm {m} ^ {2}\ cdot\ mathrm m {кг} ^ {-2}\ вправо)\ вліво (2,0\ рази 10^ {15}\ mathrm {кг}\ праворуч)} {\ ліворуч (5.0\ раз 10^ {3}\ mathrm {m}\ праворуч)}} =7.3\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}
\ кінець {вирівняний}\ номер\]
Враховуючи, що олімпійські спринтери зазвичай досягають швидкостей\(12 \mathrm{m} \cdot \mathrm{s}^{-1}\), це легка швидкість, яку можна досягти, бігаючи на землі. Торо може бути важче генерувати прискорення, необхідне для досягнення цієї швидкості, відштовхуючись від землі, оскільки будь-яка незначна висхідна сила підніме центр маси бігуна, і це займе значно більше часу, ніж на землі, щоб повернутися вниз для іншого поштовху від землі.
Приклад 14.3 Пружинний блок-петля-петля
Невеликий блок масою m притискають до пружини з пружинною постійною k і утримують на місці з уловом. Пружина стискається на невідомому відстані х (рис. 14.12). При знятті улову блок виходить з пружини і ковзає по нефрикционной круглої петлі радіусом r. Коли блок досягає вершини петлі, сила петлі на блоці (нормальна сила) дорівнює дворазовій силі гравітації на масу. (а) Використовуючи збереження енергії, знайдіть кінетичну енергію блоку у верхній частині петлі. (b) Використовуючи Другий закон Ньютона, виведіть рівняння руху для блоку, коли він знаходиться у верхній частині циклу. Зокрема, знайти швидкість через\(v_{\text {top }}\) постійну гравітації g і радіус петлі r. (c) На якій відстані була стиснута пружина?

Рішення: а) Виберіть для початкового стану момент перед випуском улову. Початкова кінетична енергія є\(K_{i}=0\). Початкова потенційна енергія ненульова,\(U_{i}=(1 / 2) k x^{2}\). Початкова механічна енергія тоді
\[E_{i}=K_{i}+U_{i}=\frac{1}{2} k x^{2} \nonumber \]
Виберіть для кінцевого стану момент, коли блок знаходиться у верхній частині циклу. Кінцева кінетична енергія є\(K_{f}=(1 / 2) m v_{\text {top }}^{2}\); блок знаходиться в русі зі швидкістю\(v_{\text {top }}\). Кінцева потенційна енергія ненульова,\(U_{f}=(m g)(2 R)\). Кінцева механічна енергія тоді
\[E_{f}=K_{f}+U_{f}=2 m g R+\frac{1}{2} m v_{\mathrm{top}}^{2} \nonumber \]
Оскільки ми припускаємо, що трек не тертя і нехтує опором повітря, немає консервативної роботи. Тому зміна механічної енергії дорівнює нулю,
\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]
Механічна енергія зберігається\(E_{f}=E_{i}\), тому
\[2 m g R+\frac{1}{2} m v_{\mathrm{top}}^{2}=\frac{1}{2} k x^{2} \nonumber \]
З Рівняння (14.8.10) кінетична енергія у верхній частині петлі дорівнює
\[\frac{1}{2} m v_{\mathrm{top}}^{2}=\frac{1}{2} k x^{2}-2 m g R \nonumber \]
б) У верхній частині петлі сили на блоці - це гравітаційна сила величини мг і нормальна сила величини N, обидві спрямовані вниз. Другий закон Ньютона в радіальному напрямку, який є напрямком вниз, є
\[-m g-N=-\frac{m v_{\mathrm{top}}^{2}}{R} \nonumber \]
У цій задачі ми даємо, що при досягненні блоком вершини петлі сила петлі на блоці (нормальна сила, вниз в даному випадку) дорівнює дворазовій вазі блоку, N = 2мг. Другий закон, рівняння (14.8.12), потім стає
\[3 m g=\frac{m v_{\mathrm{top}}^{2}}{R} \nonumber \]
Ми можемо переписати рівняння (14.8.13) з точки зору кінетичної енергії як
\[\frac{3}{2} m g R=\frac{1}{2} m v_{\mathrm{top}}^{2} \nonumber \]
Таким чином, швидкість у верхній частині
\[v_{\mathrm{top}}=\sqrt{3 m g R} \nonumber \]
в) Рівняння розчісування (14.8.11) і (14.8.14) дає
\[\frac{7}{2} m g R=\frac{1}{2} k x^{2} \nonumber \]
Таким чином, початкове зміщення пружини від рівноваги становить
\[x=\sqrt{\frac{7 m g R}{k}} \nonumber \]
Приклад 14.4 Мас-пружина на шорсткій поверхні
Блок маси m ковзає по горизонтальному столу зі швидкістю\(v_{0}\). При x = 0 він б'є пружину з постійною пружини k і починає відчувати силу тертя. Коефіцієнт тертя змінний і задається тим\(\mu=b x\), де b - позитивна константа. Знайдіть втрати механічної енергії, коли блок вперше на мить приходить в спокій.

Рішення: З моделі, наведеної для сили тертя, ми могли б знайти виконану неконсервативну роботу, яка така ж, як втрата механічної енергії, якби ми знали положення,\(x_{f}\) де блок вперше приходить у спокій. Найпрямішим (і найпростішим) способом пошуку\(x_{f}\) є використання теореми «робота-енергія». Початкова механічна енергія є\(E_{i}=m v_{i}^{2} / 2\) і кінцева механічна енергія є\(E_{f}=k x_{f}^{2} / 2\) (зверніть увагу, що немає терміна потенційної енергії в\(E_{i}\) і немає\(E_{f}\) терміна кінетичної енергії Різниця між цими двома механічними енергіями - це неконсервативна робота, виконана силою тертя,
\ [\ почати {вирівняний}
W_ {\ mathrm {nc}} &=\ int_ {x=0} ^ {x = x_ {f}} F_ {\ mathrm {nc}} d x =\ int_ {x=0} ^ {x_ {f}} -F_ {\ mathrm {тертя}} d x =\ int_ {x = 0} {x=x_ {f}} -\ му N д х\\
&=-\ int_ {0} ^ {x_ {f}} б х м г г г х =-\ розрив {1} {2} б м г x_ {f} ^ {2}
\ кінець {вирівняний}\ nonumber\]
Тоді ми маємо це
\ [\ почати {вирівняний}
W_ {\ mathrm {nc}} &=\ Дельта E_ {m}\\
W_ {\ mathrm {nc}} &=E_ {f} -E_ {i}\
-\ frac {1} {2} b m g x_ {f} ^ {2} &=\ frac {1} {2} k x_ {f} ^ {2} -\ розрив {1} {2} м v_ {i} ^ {2}
\ кінець {вирівняний}\ nonumber\]
Розв'язування останнього з цих рівнянь для\(x_{f}^{2}\) прибутковості
\[x_{f}^{2}=\frac{m v_{0}^{2}}{k+b m g} \nonumber \]
Рівняння заміни (14.8.20) в Рівняння (14.8.18) дає результат, який
\[W_{\mathrm{nc}}=-\frac{b m g}{2} \frac{m v_{0}^{2}}{k+b m g}=-\frac{m v_{0}^{2}}{2}\left(1+\frac{k}{b m g}\right)^{-1} \nonumber \]
Варто перевірити, щоб вищевказаний результат був розмірно правильним. З моделі параметр b повинен мати розміри зворотної довжини (коефіцієнт тертя\(\mu\) повинен бути безрозмірним), і тому виріб BMG має розміри сили на довжину, як і постійна пружини k; результат розмірно узгоджений.
Приклад 14.5 Візок-пружина на похилій площині
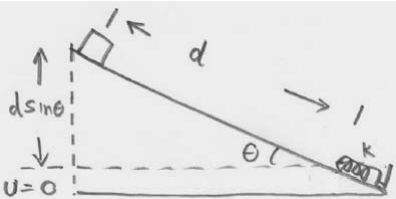
Об'єкт масою m ковзає вниз площиною, яка нахилена під кутом θ від горизонталі (рис. 14.14). Об'єкт починається в стані спокою. Центр маси візка - відстань d від нерозтягнутої пружини, яка лежить в нижній частині площини. Припустимо, що пружина безмасова, і має постійну пружину k. Припустимо, що похила площина повинна бути без тертя. (а) Як далеко пружина стиснеться, коли маса вперше прийде в спокій? (б) Тепер припустимо, що похила площина має коефіцієнт кінетичного тертя\(\mu_{\mathrm{k}}\) Як далеко пружина стиснеться, коли маса вперше прийде в спокій? Тертя в першу чергу між колесами і підшипниками, а не між візком і площиною, але сила тертя може бути змодельована коефіцієнтом тертя\(\mu_{\mathrm{k}}\). (c) У випадку (b), скільки енергії було втрачено на тертя?

Рішення: Нехай х позначає зміщення пружини з положення рівноваги. Вибирайте нульову точку для гравітаційної потенційної енергії\(U^{g}(0)=0\) не в самому низу похилій площині, а в місці розташування кінця нерозтягнутої пружини. Виберіть нульову точку для потенційної енергії пружини, де пружина знаходиться в положенні рівноваги,\(U^{s}(0)=0\)
а) Виберіть для початкового стану момент звільнення об'єкта (рис. 14.15). Початкова кінетична енергія є\(K_{i}=0\). Початкова потенційна енергія ненульова,\(U_{i}=m g d \sin \theta\). Початкова механічна енергія тоді
\[E_{i}=K_{i}+U_{i}=m g d \sin \theta \nonumber \]
Виберіть для кінцевого стану момент, коли об'єкт вперше приходить в спокій і пружина стискається на відстань x в нижній частині похилої площини (рис. 14.16). Кінцева кінетична енергія полягає в\(K_{f}=0\) тому, що маса не знаходиться в русі. Кінцева потенційна енергія ненульова,\(U_{f}=k x^{2} / 2-x m g \sin \theta\) зверніть увагу, що гравітаційна потенційна енергія негативна, оскільки об'єкт опустився нижче висоти нульової точки гравітаційної потенційної енергії.

Кінцева механічна енергія тоді
\[E_{f}=K_{f}+U_{f}=\frac{1}{2} k x^{2}-x m g \sin \theta \nonumber \]
Оскільки ми припускаємо, що трек не тертя і нехтує опором повітря, немає консервативної роботи. Тому зміна механічної енергії дорівнює нулю,
\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]
Тому
\[d m g \sin \theta=\frac{1}{2} k x^{2}-x m g \sin \theta \nonumber \]
Це квадратне рівняння в х,
\[x^{2}-\frac{2 m g \sin \theta}{k} x-\frac{2 d m g \sin \theta}{k}=0 \nonumber \]
У квадратичній формулі ми хочемо позитивного вибору квадратного кореня для розв'язку, щоб забезпечити позитивне зміщення пружини від рівноваги,
\ [\ почати {вирівняний}
х &=\ розрив {м г\ син\ тета} {k} +\ лівий (\ frac {m^ {2} g^ {2}\ sin ^ {2}\ тета} {k^ {2}}} +\ frac {2 d m g\ sin\ theta} {k}\ праворуч) ^ {1/2}\
&=\ frac {m g} {k} (\ sin\ тета+\ sqrt {1+2 (k d/м г)\ sin\ тета})
\ кінець {вирівняний}\ nonumber\]
(Що б представляло рішення з негативним коренем?)
б) Ефект кінетичного тертя полягає в тому, що зараз існує ненульова неконсервативна робота, виконана над об'єктом, який перемістився на відстань\(d+x\), задану
\[W_{\mathrm{nc}}=-f_{\mathrm{k}}(d+x)=-\mu_{\mathrm{k}} N(d+x)=-\mu_{\mathrm{k}} m g \cos \theta(d+x) \nonumber \]
Зверніть увагу, що нормальна сила знайдена за допомогою другого закону Ньютона в перпендикулярному напрямку до похилої площини,
\[N-m g \cos \theta=0 \nonumber \]
Таким чином, зміна механічної енергії
\[W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]
який стає
\[-\mu_{\mathrm{k}} m g \cos \theta(d+x)=\left(\frac{1}{2} k x^{2}-x m g \sin \theta\right)-d m g \sin \theta \nonumber \]
Рівняння (14.8.31) спрощує
\[0=\left(\frac{1}{2} k x^{2}-x m g\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)\right)-d m g\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right) \nonumber \]
Це те саме, що і Рівняння (14.8.25) вище, але з\(\sin \theta \rightarrow \sin \theta-\mu_{k} \cos \theta\). Максимальний зсув пружини - це коли є тертя, то
\[x=\frac{m g}{k}\left(\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)+\sqrt{1+2(k d / m g)\left(\sin \theta-\mu_{\mathrm{k}} \cos \theta\right)}\right) \nonumber \]
в) Енергія, втрачена на тертя, задається тим,\(W_{\mathrm{nc}}=-\mu_{\mathrm{k}} m g \cos \theta(d+x)\) де x дається в частині b).
Приклад 14.6 Ковзання об'єкта по сфері
Невелика точка, подібна до об'єкта маси m, спирається на верхню частину сфери радіусом R. Об'єкт звільняється з верхньої частини сфери з незначною швидкістю і він повільно починає ковзати (рис. 14.17). Нехай g позначають постійну гравітації. (а)\(\theta_{1}\) Визначте кут щодо вертикалі, під яким об'єкт втратить контакт з поверхнею сфери. (б) Яка швидкість\(v_{1}\) об'єкта в той момент, коли він втрачає контакт з поверхнею сфери.
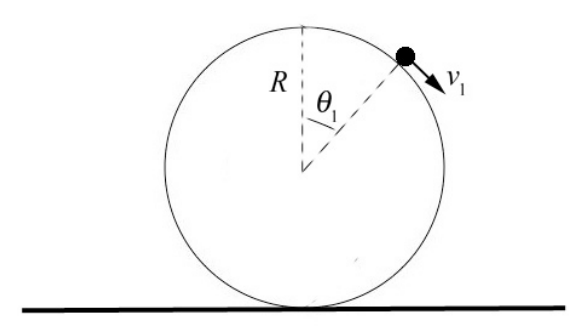
Рішення: Починаємо з виявлення сил, що діють на об'єкт. Є дві сили, що діють на об'єкт, гравітація та радіальна нормальна сила, яку сфера надає на частинку, яку ми позначаємо N. Ми намалюємо діаграму сили вільного тіла для об'єкта, поки він ковзає по сфері. Вибираємо полярні координати, як показано на малюнку 14.18.

Ключовим обмеженням є те, що коли частка просто залишає поверхню, нормальна сила дорівнює нулю,
\[N\left(\theta_{1}\right)=0 \nonumber \]
де\(\theta_{1}\) позначається кут по відношенню до вертикалі, при якому предмет просто втратить контакт з поверхнею сфери. Оскільки нормальна сила перпендикулярна зміщенню об'єкта, вона не працює на об'єкт і, отже, збереження енергії не враховує обмеження на рух, накладене нормальною силою. Для того, щоб проаналізувати вплив нормальної сили, ми повинні використовувати радіальну складову Другого закону Ньютона,
\[N-m g \cos \theta=-m \frac{v^{2}}{R} \nonumber \]
Тоді, коли об'єкт просто втрачає контакт з поверхнею, Рівняння (14.8.34) та (14.8.35) вимагають, щоб
\[m g \cos \theta_{1}=m \frac{v_{1}^{2}}{R} \nonumber \]
де\(v_{1}\) позначається швидкість об'єкта в ту мить, коли він втрачає контакт з поверхнею сфери. Зверніть увагу, що умова обмеження Рівняння (14.8.36) може бути перезаписано як
\[m g R \cos \theta_{1}=m v_{1}^{2} \nonumber \]
Тепер ми можемо застосувати збереження енергії. Виберіть нульову контрольну точку U = 0, щоб потенційна енергія була середньою точкою сфери.
Визначте початковий стан як момент звільнення об'єкта (рис. 14.19). Ми можемо знехтувати дуже маленькою початковою кінетичною енергією, необхідною для переміщення об'єкта від верхньої частини сфери тощо\(K_{i}=0\). Початкова потенційна енергія ненульова,\(U_{i}=m g R\). Початкова механічна енергія тоді
\[E_{i}=K_{i}+U_{i}=m g R \nonumber \]


Виберіть для кінцевого стану момент виходу об'єкта зі сфери (рис. 14.20). Кінцева кінетична енергія є\(K_{f}=m v_{1}^{2} / 2\); об'єкт знаходиться в русі зі швидкістю\(v_{1}\). Кінцева потенційна енергія ненульова,\(U_{f}=m g R \cos \theta_{1}\). Кінцева механічна енергія тоді
\[E_{f}=K_{f}+U_{f}=\frac{1}{2} m v_{1}^{2}+m g R \cos \theta_{1} \nonumber \]
Оскільки ми припускаємо, що контактна поверхня нефрикційна і нехтуючи опором повітря, немає ніякої неконсервативної роботи. Тому зміна механічної енергії дорівнює нулю,
\[0=W_{\mathrm{nc}}=\Delta E_{m}=E_{f}-E_{i} \nonumber \]
Тому
\[\frac{1}{2} m v_{1}^{2}+m g R \cos \theta_{1}=m g R \nonumber \]
Тепер ми вирішуємо рівняння умови обмеження (14.8.37) у рівняння (14.8.41), що дає
\[\frac{1}{2} m g R \cos \theta_{1}+m g R \cos \theta_{1}=m g R \nonumber \]
Тепер ми можемо вирішити кут, під яким об'єкт просто залишає поверхню
\[\theta_{1}=\cos ^{-1}(2 / 3) \nonumber \]
Тепер ми підставляємо цей результат у Рівняння (14.8.37) і вирішуємо для швидкості
\[v_{1}=\sqrt{2 g R / 3} \nonumber \]
