11.4: Опрацьовані приклади

Приклад 11.1 Відносні швидкості двох рухомих площин

Літак А їде на північний схід зі швидкістю$v_{\mathrm{A}}=160 \mathrm{m} \cdot \mathrm{s}^{-1}$. Другий літак B їде на південний схід зі швидкістю$v_{\mathrm{B}}=200 \mathrm{m} \cdot \mathrm{s}^{-1}$. (a) Виберіть систему координат і запишіть вираз для швидкості кожного літака як вектори,$\overrightarrow{\mathbf{V}}_{\mathrm{A}}$ і$\overrightarrow{\mathbf{V}}_{B}$ обережно використовуйте вектори одиниць, щоб висловити свою відповідь. (b) Намалюйте вектори$\overrightarrow{\mathbf{V}}_{\mathbf{A}}$ та$\overrightarrow{\mathbf{V}}_{\mathbf{B}}$ на вашій системі координат. (c) Знайти векторний вираз, який виражає швидкість літака А, як видно з спостерігача, що летить в літаку Б. Обчисліть цей вектор. Яка її величина і напрямок? Намалюйте його на вашій системі координат.

Малюнок 11.2 (b): Система координат

Спостерігач у стані спокою щодо землі визначає опорну рамку$S$. Виберіть систему координат, показану на малюнку 11.2b. За словами цього спостерігача, літак А рухається зі швидкістю$\overrightarrow{\mathbf{v}}_{\mathrm{A}}=v_{\mathrm{A}} \cos \theta_{\mathrm{A}} \hat{\mathbf{i}}+v_{\mathrm{A}} \sin \theta_{\mathrm{A}} \hat{\mathbf{j}}$, а літак В рухається зі швидкістю$\overrightarrow{\mathbf{v}}_{\mathrm{B}}=v_{\mathrm{B}} \cos \theta_{\mathrm{B}} \hat{\mathbf{i}}+v_{\mathrm{B}} \sin \theta_{\mathrm{B}} \hat{\mathbf{j}}$. Згідно з інформацією, наведеною в проблемі літак А летить на північний схід, так$\theta_{\mathrm{A}}=\pi / 4$ і літак B летить на південний схід так$\theta_{\mathrm{B}}=-\pi / 4$. Таким чином$\overrightarrow{\mathbf{v}}_{\mathrm{A}}=\left(80 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{i}}+\left(80 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{j}}$ і$\overrightarrow{\mathbf{v}}_{\mathrm{B}}=\left(100 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{i}}-\left(100 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{j}}$.

Розглянемо другого спостерігача, що рухається разом з літаком B, визначаючи опорну рамку S′. Яка швидкість літака А за даними цього спостерігача, що рухається в літаку B? Швидкість спостерігача, що рухається вздовж в літаку B по відношенню до спостерігача в стані спокою на землі є лише швидкістю літака B і задається$\overrightarrow{\mathbf{V}}=\overrightarrow{\mathbf{v}}_{\mathrm{B}}=v_{\mathrm{B}} \cos \theta_{\mathrm{B}} \hat{\mathbf{i}}+v_{\mathrm{B}} \sin \theta_{\mathrm{B}} \hat{\mathbf{j}}$. Використовуючи закон додавання швидкостей, рівняння (11.3.2), швидкість літака А щодо спостерігача, що рухається разом з літаком B, задається

\ [\ почати {вирівняний}
\ переправа стрілка {\ mathbf {v}} _ {\ mathrm {A}} ^ {\ прайм} &=\ переправа {\ mathbf {v}} _ {\ mathrm {A}} -\ переправа стрілка {\ mathbf {V}} =\ лівий (v_ {\ mathrm {A}}\ cos\ theta_ {\ mathrm {A}}\ hat {\ mathbf {i}} +v_ {\ mathrm {A}}\ sin\ theta_ {\ mathrm {A}}\ hat {\ mathbf {j}}\ праворуч) -\ ліво (v_ {\ mathrm {B}}\ cos\ тета_ {\ математика {B}}\ hat {\ mathbf {i}} +v_ {\ mathrm {B}}\ sin\ theta_ {\ mathrm {B}}\ hat {\ mathbf {j}}\ праворуч)\\
&=\ ліворуч (v_ {\ mathrm {A}}\ cos\ theta_ {m {A}} -v_ {\ mathrm {B}}\ cos\ theta_ {\ mathrm {B}}\ право)\ що {\ mathbf {i}} +\ left (v_ {\ mathrm {A}}\ sin\ theta_ {\ mathrm {A}} -v_ {\ mathrm {B}}\ sin\ theta_ _ {\ математика {B}}\ праворуч)\ капелюх {\ mathbf {j}}\\
&=\ ліворуч (\ ліворуч (80\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ вліво (100\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {s} ^ {}\ праворуч)\ праворуч)\ капелюх {\ mathbf {i}} +\ ліворуч (\ ліворуч (80\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ праворуч) +\ ліворуч (100\ sqrt {2}\ mathrm {m}\ cdot\ mathrm { s} ^ {-1}\ право)\ право)\ капелюх {\ mathbf {j}}. \\
&=-\ ліворуч (20\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ праворуч)\ капелюх {\ mathbf {i}} +\ лівий (180\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ праворуч)\ капелюх {\ mathbf {j}}\\
&=v_ {A x} ^ {\ прайм}\ капелюх {\ mathbf {я}} +v_ {A\ mathrm {y}} ^ {\ прайм}\ капелюх {\ mathbf {j}}
\ кінець {вирівняний}\ номер\]

На малюнку 11.3 показана швидкість літака А по відношенню до літака B в опорній рамці S′.

Малюнок 11.3 Літак А, як видно з спостерігача в літаку B

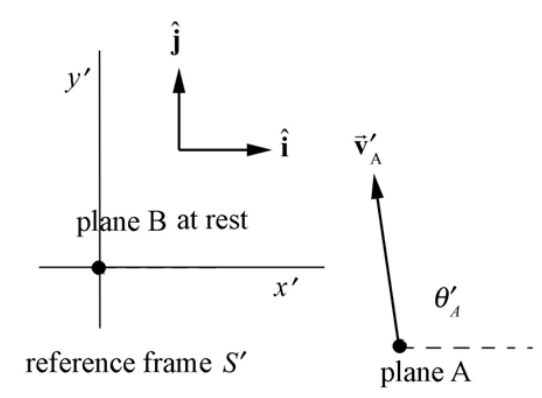
Величина швидкості літака А, яку бачить спостерігач, що рухається з літаком В, задається

$$\left|\vec{v}_{\mathrm{A}}^{\prime}\right|=\left(v_{A x}^{\prime 2}+v_{A y}^{\prime 2}\right)^{1 / 2}=\left(\left(-20 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right)^{2}+\left(180 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right)^{2}\right)^{1 / 2}=256 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber$$

Кут швидкості літака А, який бачить спостерігач, що рухається з літаком B, задається,

\ [\ почати {вирівняний}
\ theta_ {A} ^ {\ прайм} &=\ тан ^ {-1}\ ліворуч (v_ {A y} ^ {\ прайм}/v_ {A x} ^ {\ прайм}\ праворуч) =\ тан ^ {-1}\ ліворуч (180\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} {-1}\ праворуч)/\ ліворуч (-20\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ праворуч)\\
&=\ tan ^ {-1} (-9) =180^ {\ circ} -83. 7^ {\ circ} =96.3^ {\ circ}
\ кінець {вирівняний}\ nonumber\]

Приклад 11.2 Відносний рух і полярні координати

Під відносною швидкістю ми маємо на увазі швидкість по відношенню до заданої системи координат. (Термін швидкість, поодинці, розуміється відносно системи координат спостерігача.) (a) Спостерігається, що точка має швидкість$\overrightarrow{\mathbf{V}}_{A}$, відносно системи координат A. Яка його швидкість щодо системи координат B, яка зміщується від системи А на відстань$\overrightarrow{\mathbf{R}}$? $(\overrightarrow{\mathbf{R}}$може змінюватися в часі.) (b) Частинки a і b рухаються в протилежних напрямках по колу з величиною кутової швидкості ω, як показано на малюнку 11.4. При t = 0 вони обидва знаходяться в точці,$\overrightarrow{\mathbf{r}}=\hat{l} \hat{\mathbf{j}}$ де l - радіус кола. Знайти швидкість a щодо b.

Малюнок 11.5 Частки a і b, що рухаються відносно один одного

Рішення: (a) Вектори положення пов'язані

$$\overrightarrow{\mathbf{r}}_{B}=\overrightarrow{\mathbf{r}}_{A}-\overrightarrow{\mathbf{R}} \nonumber$$

Швидкості пов'язані шляхом взяття похідних, (закон додавання швидкостей Рівняння (11.3.2))

$$\overrightarrow{\mathbf{v}}_{B}=\overrightarrow{\mathbf{v}}_{A}-\overrightarrow{\mathbf{V}} \nonumber$$

(b) Давайте виберемо два опорні кадри; кадр B зосереджений на частинці b, а кадр A - по центру кола на малюнку 11.5. Тоді вектор взаємного положення між витоками двох кадрів задається

$$\overrightarrow{\mathbf{R}}=l \hat{\mathbf{r}} \nonumber$$

Вектор положення частинки a відносно кадру A задається

$$\overrightarrow{\mathbf{r}}_{A}=l \hat{\mathbf{r}}^{\prime} \nonumber$$

Вектор положення частинки b у кадрі B можна знайти шляхом підстановки рівнянь (11.4.7) та (11.4.6) на Рівняння (11.4.4),

$$\overrightarrow{\mathbf{r}}_{B}=\overrightarrow{\mathbf{r}}_{A}-\overrightarrow{\mathbf{R}}=l \hat{\mathbf{r}}^{\prime}-l \hat{\mathbf{r}} \nonumber$$

Ми можемо розкласти кожен$\hat{\mathbf{r}}^{\prime}$ з одиничних векторів$\hat{\mathbf{r}}$ і щодо декартових одиничних векторів$\hat{\mathbf{1}}$ і$\hat{\mathbf{j}}$ (див. Рис. 11.5),

$$\hat{\mathbf{r}}=-\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}} \nonumber$$

$$\hat{\mathbf{r}}^{\prime}=\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}} \nonumber$$

Тоді рівняння (11.4.8), що дає вектор положення частинки b у кадрі B, стає

$$\overrightarrow{\mathbf{r}}_{B}=l \hat{\mathbf{r}}^{\prime}-l \hat{\mathbf{r}}=l(\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}})-l(-\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}})=2 l \sin \theta \hat{\mathbf{i}} \nonumber$$

Для того, щоб знайти вектор швидкості частинки a в кадрі B (тобто по відношенню до частинки b), диференціюють рівняння (11.4.11)

$$\overrightarrow{\mathbf{v}}_{B}=\frac{d}{d t}(2 l \sin \theta) \hat{\mathbf{i}}=(2 l \cos \theta) \frac{d \theta}{d t} \hat{\mathbf{i}}=2 \omega l \cos \theta \hat{\mathbf{i}} \nonumber$$

Приклад 11.3 Віддача в різних кадрах

Людина масового$m_{1}$ стоїть на возі маси$m_{2}$. Припустимо, що візок вільно переміщатися на своїх колесах без тертя. Людина кидає м'яч маси$m_{3}$ θ по відношенню до горизонталі, виміряної людиною у візку. М'яч кидається$v_{0}$ зі швидкістю по відношенню до візка (рис. 11.6). (а) Яка кінцева швидкість кулі, як бачить спостерігач, закріплений на землі? (b) Яка кінцева швидкість візка, яку бачить спостерігач, закріплений на землі? (c) Що стосується горизонталі, який кут фіксованого спостерігача бачить м'яч покинути візок?

Малюнок 11.6 Віддача людини на возі через кинутого м'яча

Рішення: а), б) Наша опорна рамка буде такою, що закріплена на землі. Ми візьмемо як наш початковий стан, що перед тим, як м'яч буде кинутий (візок, м'яч, кидає людина нерухомий) і наш остаточний стан, що після м'яча кидається. Ми припускаємо, що тертя немає, і тому немає зовнішніх сил, що діють в горизонтальному напрямку. Початкова x -складова сумарного імпульсу дорівнює нулю,

$p_{x, 0}=0$всього

Після того, як м'яч буде кинутий, візок і людина мають кінцевий імпульс

$$\overrightarrow{\mathbf{p}}_{f, \text { cart }}=-\left(m_{2}+m_{1}\right) v_{f, \text { cart }} \hat{\mathbf{i}} \nonumber$$

як вимірюється людиною на землі,$v_{f, cart}=0$ де швидкість людини і візка. (Центр маси людини буде рухатися щодо візка, поки м'яч кидається, але оскільки нас цікавлять швидкості, а не позиції, нам потрібно лише припустити, що людина перебуває у стані спокою щодо візка після того, як м'яч кинутий.)

М'яч кидається зі швидкістю$v_{0}$ і під кутом θ по відношенню до горизонталі, що вимірюється людиною у візку. Тому людина у візку кидає м'яч зі швидкістю.

$$\overrightarrow{\mathbf{v}}_{f, \text { ball }}^{\prime}=v_{0} \cos \theta \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}} \nonumber$$

Оскільки візок рухається у негативному напрямку x зі швидкістю так$v_{f, cart}=0$ само, як м'яч залишає руку людини, х -компонент швидкості кулі, виміряний спостерігачем на землі, задається

$$v_{x f, \text { ball }}=v_{0} \cos \theta-v_{f, \text { cart }} \nonumber$$

М'яч, здається, має меншу х -складову швидкості відповідно до спостерігача на землі. Швидкість кулі, виміряна спостерігачем на землі, становить

$$\overrightarrow{\mathbf{v}}_{f, \text { ball }}=\left(v_{0} \cos \theta-v_{f, \text { cart }}\right) \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}} \nonumber$$

Кінцевий імпульс м'яча, за словами спостерігача на землі, становить

$$\overrightarrow{\mathbf{p}}_{f, \text { ball }}=m_{3}\left[\left(v_{0} \cos \theta-v_{f, \text { can }}\right) \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}}\right] \nonumber$$

Схема руху імпульсу показана на (рис. 11.7).

Малюнок 11.7 Схема руху імпульсу для віддачі

Оскільки х -компонент імпульсу системи є постійним, ми маємо що

\ [\ почати {вирівняний}
0 &=\ ліворуч (p_ {x, f}\ праворуч) _ {\ текст {кошик}} +\ ліворуч (p_ {x, f}\ праворуч) _ {\ текст {куля}}\
&=-\ ліворуч (m_ {2} +m_ {1}\ праворуч) v_ {f,\ текст {кошик}} +m_ {3}\ (v_ {0}\ cos\ тета-v_ {f,\ text {кошик}}\ праворуч)
\ кінець {вирівняний}\ nonumber\]

Ми можемо вирішити Рівняння (11.4.19) для кінцевої швидкості та швидкості візка, виміряної спостерігачем на землі,

$$v_{f, \text { cart }}=\frac{m_{3} v_{0} \cos \theta}{m_{2}+m_{1}+m_{3}} \nonumber$$

$$\overrightarrow{\mathbf{v}}_{f, \text { cart }}=v_{f, \text { cart }} \hat{\mathbf{i}}=\frac{m_{3} v_{0} \cos \theta}{m_{2}+m_{1}+m_{3}} \hat{\mathbf{i}} \nonumber$$

Зверніть увагу, що y -компонент імпульсу не є постійним, оскільки, коли людина кидає м'яч, він або вона відштовхує від візка, а нормальна сила з землею перевищує гравітаційну силу, тому чиста зовнішня сила в напрямку y - ненульова.

Заміна рівняння (11.4.20) у рівняння (11.4.17) дає

\ [\ почати {вирівняний}
\ overrightarrow {\ mathbf {v}} _ {f,\ текст {м'яч}} &=\ ліворуч (v_ {0}\ cos\ theta-v_ {f,\ text {кошик}}\ праворуч)\ капелюх {\ mathbf {i}} +v_ {0}\ sin\ тета\ капелюх {\ mathbf {j}}\\
&=\ розрив {m_ {1} +m_ {2}} {m_ {1} +m_ {2} +m_ {3}}\ лівий (v_ {0}\ cos\ тета\ праворуч)\ капелюх {\ mathbf {i}} +\ лівий (v_ {0}\ sin\ тета\ право)\ hat {\ mathbf {j}}
\ кінець {вирівняний}\ nonumber\]

Як перевірку, зверніть увагу, що в межі$m_{3}<<m_{1}+m_{2}$,$\overrightarrow{\mathbf{V}} f, \text { ball }$ має швидкість$v_{0}$ і спрямований під кутом θ вище горизонталі; той факт, що набагато більш масивна комбінація людина-візок вільно рухатися не впливає на політ м'яча, як бачить фіксований спостерігач. Також врахуйте, що в$m>>m_{1}+m_{2}$ нереальному межі м'яч рухається зі швидкістю набагато меншою, ніж у$v_{0}$ міру виходу з візка.

в) Кут,$\phi$ під яким м'яч кидається, як бачить спостерігач на землю, задається

\ [\ почати {вирівняний}
\ phi &=\ тан ^ {-1}\ розрив {\ ліворуч (v_ {f,\ текст {м'яч}}\ вправо) _ {y}} {\ лівий (v_ {f,\ text {м'яч}}\ вправо) _ {x}} =\ тан ^ {-1}\ frac {v_ {0}\ sin\ theta} {\ left (m_ {1} +m_ {2}\ праворуч)/\ ліворуч (m_ {1} +m_ {2} +m_ {3}\ праворуч)\ праворуч] v_ {0}\ cos\ тета}\\
&=\ тан ^ {-1}\ лівий [\ лівий (\ розрив {m_ {1} +m_ {2} +m_ {3}} {m_ {1} +m_ {2}}\ праворуч)\ тан\ тета\ праворуч]
\ кінець {вирівняний}\ nonumber\]

Для довільних значень для мас вищевказане вираз не буде зводитися до спрощеного вигляду. Однак ми можемо бачити, що$\tan \phi>\tan \theta$ для довільних мас, і що в межі$m_{3}<<m_{1}+m_{2}, \phi \rightarrow \theta$ і в нереальному межі$m_{3} \gg m_{1}+m_{2}, \phi \rightarrow \pi / 2$. Чи можете ви пояснити це останнє непарне передбачення?