13.14: Експеримент Штерна-Герлаха

Ця сторінка узагальнює класичний експеримент Штерна-Герлаха на «спині» і розширює лікування до обговорення кореляційних експериментів. Як це часто буває, я створюю максимальну складність, вивчаючи експериментальні деталі, а потім ховаю їх у «коробці». На цей раз коробка вийде буквальною.

Тут ми концентруємося на електрони, які мають всього два спін-стану. Ми також згадуємо фотони, які також мають два спін-стани. Підхід значною мірою базується на одному Фейнмана, який він використовував для об'єктів з трьома спінових станів: див. Р.П. Фейнман, Р.Б. Лейтон і М. Сендс, Лекції Фейнмана з фізики, Том III, глава 5 для цієї дискусії.

Класичні заряджені спінінг об'єкти

Почнемо з розгляду макроскопічного зарядженого кулі, який кидається між полюсами магніту. Якщо м'яч не крутиться, «кастет» до бейсбольного вентилятора, він не буде відхилений. Однак, якщо він обертається, він буде відхилений, як показано:

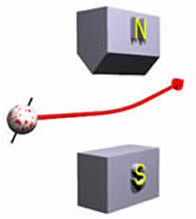
Ми ігноруємо:

• Дивна форма магнітних полюсних частин.
• Справа в тому, що будуть горизонтальні прогини. Їх можна скасувати, поставивши електричне поле перпендикулярно площині траєкторії м'яча.

Для випадку, показаного вище, цифра праворуч показує обертання заряду. Ми назвемо цю орієнтацію «обертатися», оскільки вона відхиляється магнітами вгору. Загальна величина прогину є функцією

• Загальна кількість і розподіл електричного заряду по кулі.
• Орієнтація і швидкість віджиму. Зі збільшенням швидкості віджиму зростає і прогин. Оскільки вісь спина стає більш вертикальною, ця величина відхилення також збільшується.

На відміну від цього, електрон «обертається вниз» матиме свою орієнтацію на обертання, як показано нижче:

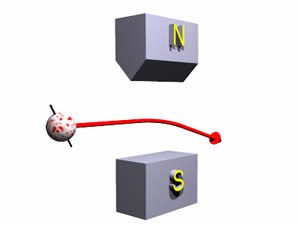
Такий предмет відхиляється вниз магнітами.

Все вищесказане - це лише класична електрика 19 століття і магнетизм.

Спін електрона

Якщо промінь від електронної гармати спрямований на магніти, як показано праворуч, промінь розбивається на дві частини. Одна половина електронів в пучку відхилена вгору, інша половина відхилена вниз. Величина прогину вгору або вниз точно така ж величина. Чи відхиляється окремий електрон вгору або вниз, здається випадковим. Стерн і Герлах зробили версію цього експерименту в 1922 році.

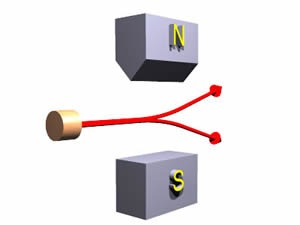
Це дуже загадково. Здається, що «спина» електронів настає всього в двох станах. Якщо правильно припустити, що швидкість обертання, загальний заряд і розподіл заряду всіх електронів однакові, то, очевидно, величина кута, який робить вісь спина з горизонталлю, однакова для всіх електронів. Для одних електронів вісь спіна - це те, що ми називаємо «спина вгору», для інших «спина вниз».

Слід остерігатися терміна «спина». Якщо використовувати «класичний радіус електрона» і відомий сумарний момент моменту електрона, то легко обчислити, що точка на екваторі електрона рухається приблизно в 137 разів більше швидкості світла! Таким чином, хоча ми будемо продовжувати використовувати слово «спина», це дійсно скорочення для «внутрішнього кутового імпульсу».

Побудова фільтра віджиму

Як і обіцяли на початку, тепер ми трохи ускладнюємо ситуацію. Розглянемо розташування, показане праворуч:

Зверніть увагу, що полярність середнього довшого магніту зворотна від двох інших. Ми також намалювали шлях об'єкта «spin up». Коли об'єкт виходить з магнітів, він йде в тому ж напрямку, що і до того, як він увійшов в них з тією ж швидкістю.

Флеш-анімацію цього випадку можна переглянути, натиснувши тут.

Шляхом об'єкта «спина вниз» є:

Для пучка електронів одна половина піде по верхньому шляху, а інша половина буде слідувати нижньому шляху:

Нарешті, ми уявляємо, як поставити невеликий блок свинцю на шляху «спина вниз» електронів.

Тут одна половина падаючого пучка, спін-вниз електрони, буде зупинена всередині апарату, в той час як всі спін-вгору електрони будуть з'являтися в тому ж напрямку, що і до того, як вони увійшли в магніти, і з тією ж швидкістю. Таким чином, це «фільтр», який відбирає спін-ап електрони.

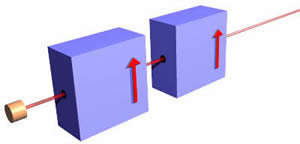
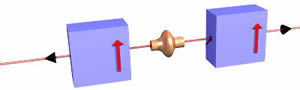
Тепер знову, як і обіцяли, ми спрощуємо, взявши всі три магніти і промінь стопор і помістивши його в коробку. На малюнку ми також включили електронну гармату, що стріляє пучком електронів по коробці. Так вийде половина падаючого пучка електронів. Важливо буде помітити, що ми намалювали стрілку на лицьовій стороні коробки, щоб вказати, який напрямок «вгору». Ви ще не бачите його, але на задній частині коробки також є стрілка, що вказує в тому ж напрямку.

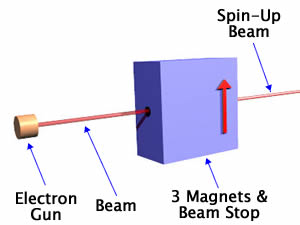
Використання фільтра віджиму

Зверніть увагу, що одна половина падаючого пучка електронів на фільтрі виходять з коробки, а інша половина - ні. Це не залежить від орієнтації фільтра; у всіх орієнтаціях, показаних нижче, одна половина падаючих електронів виходить, а інша половина - ні.

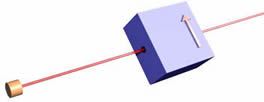
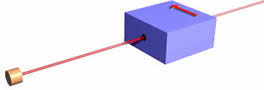
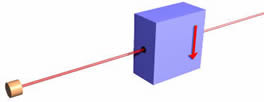
Очевидно, напрямок «вгору» визначається орієнтацією фільтра, який робить вимірювання. Це іноді називають просторовим квантуванням, термін, який мені не подобається.

Тепер ставимо другий фільтр позаду першого з такою ж орієнтацією. Другий фільтр не робить ніякого ефекту. Половина електронів з електронної гармати виходять з першого ящика, і всі ці електрони проходять через другий фільтр. Отже, як тільки «вгору» визначається першим фільтром, він збігається з «вгору», який визначається другим.
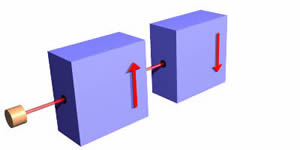
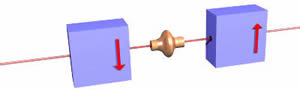
Тепер ставимо другий фільтр позаду першого і догори дном щодо першого. Як завжди, половина пучка електронів з електронної гармати виходить з першого фільтра, і жоден з цих електронів не виходить з другого фільтра. Отже, очевидно, коли перший фільтр визначає «вгору», це визначення є визначенням другого фільтра «вниз».
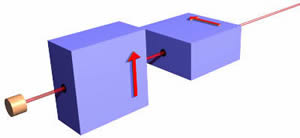
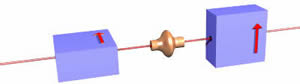
Ось ще одна орієнтація для другого фільтра, на цей раз орієнтована на 90° відносно першого. Щоб повторити ще раз, половина пучка електронів з електронної гармати виходить з першого фільтра. Виходить, що половина цих електронів проходить через другий фільтр. Отже, якщо у нас є два визначення «вгору» з двох фільтрів під прямим кутом один до одного, одна половина електронів задовольнить обидва визначення.

Якщо повільно обертати орієнтацію другого фільтра щодо першого від нуля градусів до 180 градусів, то частка електронів, які пройшли перший фільтр, що потрапляють через другий фільтр, безперервно йде від 100% до 0%.

Технічна примітка: якщо відносний кут дорівнює A, відсоток становить 100 cos ² (A/2).

Все вищесказане може нагадати вам про поляроїдних фільтрах для світла. Одна половина променя світла від, скажімо, лампи розжарювання буде проходити через такий фільтр. Якщо другий фільтр розміщений позаду першого з однаковою орієнтацією, все світло від першого фільтра проходить через другий (принаймні, у випадку ідеальних поляроїдних фільтрів). Короткий підсумок поляризації світла з'являється тут.

Якщо відносна орієнтація двох поляроїдних фільтрів для світла становить 90°, то з другого фільтра не виходить світло. Це відповідає описаному вище випадку для електронних фільтрів, коли відносна орієнтація становить 180°.

Якщо відносна орієнтація двох поляроїдних фільтрів для світла становить 45°, одна половина світла від першого фільтра вийде з другого. Це відповідає описаному вище випадку для електронних фільтрів, коли відносна орієнтація становить 90°.

Зроблено висновок, що єдина різниця між електронними та світловими фільтрами - це коефіцієнт 2 у відносних орієнтаціях. Таким чином, часто ми називаємо електронні фільтри «поляризаторами».

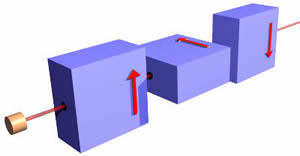
Ось останній приклад комбінування електронних фільтрів. Половина променя з електронної гармати виходить з першого поляризатора; половина цих електронів виходить з другого фільтра. І половина цих електронів зробить це через третій перевернутий фільтр! Зверніть увагу, що якщо другого фільтра не було, то з перевернутого фільтра не з'являться електрони. Таким чином, ми бачимо, що середній фільтр насправді змінює визначення «вгору» для електронів. Це ще один прояв принципу невизначеності Гейзенберга.

Підготовлено флеш-анімацію до 3 з цих фільтрів Штерна-Герлаха. Він вимагає Flash 7, і має розмір файлу 130k. Вона з'явиться в окремому вікні. Щоб отримати доступ до анімації, натисніть тут.

Кореляційні вимірювання

Ми уявляємо радіоактивну речовину, яка випромінює по парі електронів в кожному розпаді. Ці два електрони йдуть в протилежних напрямках і випромінюються майже одночасно. Коли інше ядро в зразку розпадається, інша пара електронів випромінюється майже одночасно і в протилежних напрямках. Таким чином, ми можемо мати зразок, що випромінює ці пари електронів. Праворуч покажемо такий зразок, укладений в мідний кольоровий прилад, і електронні фільтри, що вимірюють спін кожного члена пари:

Для радіоактивної речовини, яку ми будемо розглядати тут, половина електронів, що падають на правий фільтр, виходить, а половина - ні. Аналогічно виходить половина електронів, що падають на лівий фільтр, а половина - ні.

Але якщо ми подивимося на кореляцію між цими електронами, то виявимо, що якщо, скажімо, правий електрон дійсно проходить через фільтр, то його лівий супутник не пропускає його фільтри. Аналогічно, якщо правий електрон не проходить через фільтр, то з його фільтра завжди виходить його лівий супутник.

Ми говоримо, що кожен радіоактивний розпад має загальний спін нуля: якщо один електрон обертається вгору, його супутник обертається вниз. Звичайно, це за умови, що обидва фільтри мають однакове визначення вгору.

Праворуч - випадок, коли два фільтри мають протилежні визначення вгору. Знову ж половина правої руки електронів проходить через їх фільтр, а половина електронів лівої руки проходить через їх фільтр. Але цього разу, якщо конкретний правий електрон проходить свій фільтр, то його супутник лівої руки електрон завжди проходить його фільтр. Аналогічно, якщо правий електрон не проходить свій фільтр, його супутній електрон також не проходить через його фільтр.
Тепер розглянемо ще один приклад. Два фільтри визначають «вгору», щоб бути в перпендикулярних напрямках один до одного. Якщо ви все ще стежите за цим бізнесом з електронними фільтрами, ви не здивуєтеся, дізнавшись, що: Половина електронів правої руки виходить з їх фільтра. Половина електронів лівої руки виходить з їх фільтра. Якщо певний правий електрон проходить свій фільтр, то половину часу його супутник лівої руки електрон вийде з його фільтра, половину часу він не буде.
Такі види вимірювань називаються кореляційними експериментами. Ми показуємо довільну відносну орієнтацію двох фільтрів.

Ми підсумуємо все вищесказане, сказавши, що коли два фільтри мають однакову орієнтацію, кореляція дорівнює нулю: якщо правий електрон проходить, його супутник не робить. Коли два фільтри мають протилежні орієнтації, кореляція становить 100%: якщо правий електрон проходить, то і його супутник, тоді як якщо правий електрон не проходить, то і його супутник не проходить. Коли два фільтри мають перпендикулярні орієнтації, кореляція становить 50%. Виявляється, що кореляція плавно йде від нуля до 100%, оскільки відносна орієнтація йде від 0° до 180°. Для математичного студента фактична формула полягає в тому, що кореляція гріх (a /2) у квадраті, де a - відносний кут між фільтрами.

Існують радіоактивні речовини, які випромінюють пари фотонів, аналогічні парам електронів, які ми розглядали досі. Деякі такі речовини мають аналогічні кореляції з розглянутим нами джерелом електронів, за винятком того, що існує різниця в множник два у відносних орієнтаціях поляризаторів. Якщо поляризатори світла мають однакову орієнтацію, кореляція дорівнює нулю; це те ж саме, що і для електронів.

Якщо поляризатори світла мають відносну орієнтацію 90°, кореляція становить 100%: якщо фотон правої руки проходить через його поляризатор, фотон супутника пройде його поляризатори, тоді як якщо правий фотон не проходить, також не проходить його супутник. Це відповідає випадку для електронів, де відносна орієнтація фільтрів становила 180°.

Аналогічно, якщо ви все ще дотримуєтесь усього цього, кореляція, коли відносна орієнтація поляризаторів світла становить 45°, становить 50%, лише кореляція для електрона з відносними орієнтаціями фільтрів 90°.

Як ми побачимо, ці кореляційні експерименти, як для електронів, так і для фотонів, були виконані і виявляються, щоб дати нам важливу інформацію про те, як світ складається разом. Це тяга теореми Белла, також іноді відомої як парадокс Ейнштейна-Подільського-Розена (ЕПР).