13.12: Квантова телепортація

ВСТУП

У березні 1993 року Чарльз Беннетт з IBM запропонував схему, засновану на квантовій механіці, яка в принципі може бути використана для телепортації об'єкта. Схема була експериментально перевірена Діком Bouwmeester et al. восени 1997 року. У 2004 році дослідники Віденського університету та Австрійської академії наук використовували оптичне волокно довжиною 800 м, що подається через тунель громадської каналізаційної системи, щоб з'єднати лабораторії на протилежних боках річки Дунай для досягнення такої телепортації..

Тут ми досліджуємо це явище квантової телепортації. Потім ми поширимо дискусію на квантову інформацію та квантову криптографію. Документ заснований на обговоренні з верхнім курсом сучасної фізики без математики в Університеті Торонто.

Хоча обговорення майже повністю нематематичне, воно вимагає значного розуміння експериментів квантової кореляції, що використовуються при описі теореми Белла.

ТЕЛЕПОРТАЦІЇ

У Зоряному шляху, коли капітан Кірк промінюється з зорельота Ентерпрайз на поверхню планети, капітан Кірк дематеріалізується на підприємстві, а потім знову матеріалізується на планеті. На телешоу питання без відповіді полягає в тому, чи фізично транспортер розбирає капітана Кірка, переміщує атоми зі свого тіла на планету, а потім заново збирає їх. Ще однією, можливо, більш розумною альтернативою було б сканування всієї інформації про фізичний стан капітана Кірка та передача цієї інформації на поверхню планети, де вона використовується для побудови нового капітана Кірка з сировини, знайденої на планеті. Зверніть увагу, що в будь-якому випадку транспортеру потрібно мати повну інформацію про фізичний стан Кірка, щоб його реконструювати.

Однак принцип невизначеності Гейзенберга означає, що неможливо отримати цю повну інформацію про Кірка. Таким чином, здається, що найкраще, що може зробити транспортер, - це зробити приблизну копію його на поверхні планети. Квантова телепортація забезпечує спосіб «перемогти» Принцип невизначеності та зробити точну копію.

Як ми побачимо, механізм, який перевершує принцип невизначеності, той самий, який використовується для його перемоги в експериментах з квантової кореляції, які ми розглядали, коли обговорювали теорему Белла. Ми також побачимо, що хоча колапс стану для двох вимірювань у кореляційних експериментах відбувається миттєво, телепортація не може відбуватися швидше, ніж швидкість світла.

Нарешті, трохи термінології. Перш ніж ми обговорювали експерименти з квантової кореляції, в яких ми вимірювали спини двох окремих електронів, загальний спін яких дорівнював нулю. Ми називаємо стани цих двох електронів заплутаними.

ВИМІРЮВАННЯ СТАНУ ДЗВОНУ

У попередніх дискусіях ми майже завжди говорили про спіновий стан електронів, хоча ми регулярно вказували, що однакові ситуації існують і для поляризації світла, хоча і з різницею в коефіцієнт 2 в кутах, що використовуються. Тут ми змінимо ситуацію, і в основному поговоримо про станах поляризації для фотонів, хоча аргументи стосуються і спінових станів електронів.

Той факт, що ми можемо говорити про поляризацію світла майже так само, як ми обговорюємо електронний спін, не випадково. Виявляється, фотони мають спини, які можуть існувати лише в двох різних станах. І ці різні спини стани пов'язані з поляризацією світла, коли ми думаємо про це як про хвилю.

Тут ми підготуємо пари заплутаних фотонів з протилежними поляризаціями, назвемо їх Е1 і Е2. Обплутування означає, що якщо ми виміряємо пучок, скажімо, фотонів Е1 з поляризатором, половина падаючих фотонів буде пропускати фільтр незалежно від орієнтації поляризатора. Чи буде певний фотон проходити фільтр випадковим чином. Однак якщо виміряти його супутник E2 фотон поляризатором, орієнтованим на 90 градусів щодо першого, то якщо Е1 пройде його фільтр Е2 також буде пропускати його фільтр. Аналогічно, якщо Е1 не пройде свій фільтр, його супутник Е2 не буде.

Раніше ми обговорювали експеримент Майкельсона-Морлі, а пізніше інтерферометр Маха-Цендера. Ви нагадаєте, що для обох цих у нас були напівпосріблені дзеркала, які відбивають половину падаючого на них світла, а другу половину передають без відображення. Ці дзеркала іноді називають розгалужувачами променя, оскільки вони розділяють світловий промінь на дві рівні частини.

Ми будемо використовувати напівсріблене дзеркало для виконання вимірювань стану Белла. Назва - на честь винуватця теореми Белла.

Направляємо один з заплутаних фотонів, скажімо Е1, на променевий розгалужувач. Тим часом готуємо ще один фотон з поляризацією 45 ^0, і направляємо його на той же променевий розгалужувач з іншого боку, як показано на малюнку. Це фотон, властивості якого будуть транспортуватися; ми маркуємо його K (для Кірка). Уточнюємо його так, щоб і Е1, і К дісталися до променевого розгалужувача одночасно.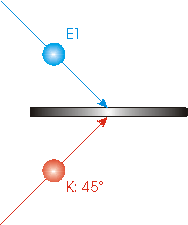
Е1 фотон, що падає зверху, буде відображатися променевим розгалужувачем деякий час і буде передаватися деякий час. Аналогічно для K фотона, який падає знизу. Так що іноді обидва фотони в кінцевому підсумку піднімаються вгору і вправо, як показано. Аналогічно, іноді обидва фотони в кінцевому підсумку йдуть вниз і вправо.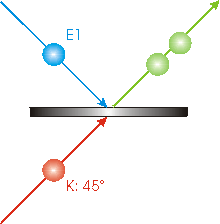
Але іноді один фотон в кінцевому підсумку підніметься вгору, а інший - вниз, як показано. Це станеться, коли обидва фотони були відбиті або обидва фотони були передані. Таким чином, існує три можливі механізми для фотонів від променевого розгалужувача: як вгору, так і вниз, або один вгору і один вниз. Яка з цих трьох можливостей виникла, можна визначити, якщо поставити детектори в шляхи фотонів після того, як вони вийшли з розгалужувача світла. Однак у випадку, якщо один фотон йде вгору, а інший йде вниз, ми не можемо сказати, який є який. Можливо, обидва фотони відбивалися променевим розгалужувачем, але, можливо, обидва були передані. Це означає, що два фотони заплуталися. Якщо у нас є великий промінь ідентично підготовлених пар фотонів, що падають на променевий розгалужувач, випадок одного фотона, що закінчується вгору, а інший вниз відбувається, можливо, дивно, 25% випадків.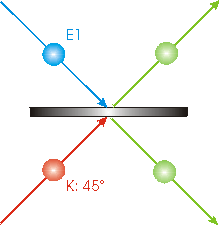

Також дещо дивно, що для однієї пари фотонів, що падають на променевий розгалужувач, фотон Е1 тепер згорнувся в стан, коли його поляризація дорівнює -45 ⁰, протилежна поляризація підготовленого 45 ⁰ одиниці. Це відбувається тому, що фотони заплуталися. Тож, хоча ми не знаємо, який фотон, ми знаємо поляризації обох.

Пояснення цих двох дещо дивовижних результатів виходить за межі цього обговорення, але може бути пояснено фазовими зміщеннями світла, що переживає світло при відображенні, сумішшю поляризаційних станів Е1 та наслідком втручання між два фотони.

ТЕЛЕПОРТ

Тепер подумаємо про супутник Е2 до E1.

25 відсотків часу вимірювання стану дзвону призвело до показаної обставини, і в цих випадках ми згорнули стан фотона Е1 в стан, де його поляризація становить -45 ⁰.

Але оскільки дві фотонні системи E1 і E2 були підготовлені з протилежними поляризаціями, це означає, що супутник E1 , E2, тепер має поляризацію +45 ⁰. Таким чином, стан фотона К тепер був перенесений на фотон Е2. Ми телепортували інформацію про фотон К в Е2.

Незважаючи на те, що цей колапс E2 у стані поляризації 45 ⁰ відбувається миттєво, ми не досягли телепортації, поки не повідомляємо, що вимірювання стану дзвінка дало показаний результат. Таким чином, телепортація не відбувається миттєво.

Відзначимо, що телепортація знищила стан вихідного K фотона.

Квантові заплутування, такі як існують між E1 та E2, в принципі, не залежать від того, наскільки далеко один від одного стають два фотони. Це було експериментально перевірено на відстані до 10 км. Таким чином, квантова телепортація аналогічно незалежна від відстані.

Початковий стан телепортованого фотона має бути знищено

Вище ми побачили, що стан фотона К було зруйновано, коли фотон Е2 придбав його. Подумайте на мить, що це було не так, тому ми отримуємо два фотони з однаковими станами поляризації. Тоді ми могли б виміряти поляризацію одного з фотонів при, скажімо, 45 ⁰, а іншого фотона при 22,5 ⁰. Тоді ми б знали стан поляризації обох фотонів для обох цих кутів.

Як ми бачили в нашому обговоренні теореми Белла, принцип невизначеності Гейзенберга говорить, що це неможливо: ми ніколи не можемо знати поляризацію фотона для цих двох кутів. Таким чином, будь-який телепорт повинен знищити стан телепортується об'єкта.

ІНШІ ПРОГРАМИ

Телепортація стану поляризації одного фотона чверть часу - це довгий шлях від надійного телепортування капітана Кірка. Однак є й інші програми вищевказаного роду апаратів, які можуть бути ближче до корисного.

Квантова інформація

Як ви напевно знаєте, комп'ютери зберігають інформацію у вигляді послідовностей 0 і 1, Наприклад, в кодуванні ASCII буква А представлена цифрою 65. Як двійкове число це:

1 000 001

Усередині комп'ютера є транзистори, які або включені, або вимкнені, і ми призначаємо включеному стані бути 1 і вимкнений стан 0. Однак одна і та ж інформація може зберігатися точно таким же чином в будь-якій системі, яка має два взаємовиключних бінарних стану.

Наприклад, якщо у нас є колекційні фотони, ми могли б представляти 1 як фотони, поляризація яких дорівнює+45 ⁰, а 0 як поляризації -45 ⁰. Ми могли б аналогічно використовувати електрони зі станами спін-вгору і спін-вниз для кодування інформації. Ці квантові біти інформації називаються кубітами.

Вище ми думали про апарат для квантової телепортації. Тепер ми бачимо, що ми можемо думати про той самий апарат, що і передача квантової інформації. Відзначимо, що, на відміну від, скажімо, факсу, при передачі Квантової інформації оригінал, поляризація фотона К, руйнується.

Квантова криптографія

Криптографія залежить як від відправника, так і від одержувача зашифрованої інформації, знаючи ключ. Відправник використовує ключ для шифрування інформації, а одержувач використовує той самий ключ для її розшифрування.

Ключ може бути чимось дуже простим, наприклад, обидві сторони знають, що кожна буква була зрушена вгору на 13 місць, а літери вище тринадцятого в алфавіті повернуті до початку. Або вони можуть бути дуже складними, наприклад, дуже довгим рядком двійкових цифр.

Ось приклад використання двійкових чисел для шифрування та розшифрування повідомлення, в даному випадку буква A, яку ми бачили, становить 1,000,001 в двійковому кодуванні ASCII. Ми будемо використовувати в якості ключа число 23, яке в двійковій системі дорівнює 0,010,111. Ми будемо використовувати ключ для кодування літери, використовуючи правило, що якщо відповідні біти літери і ключ однакові, результат дорівнює 1, а в іншому випадку 0.

A	1	0	0	0	0	0	1
Ключ	0	0	1	0	1	1	1
Зашифрований	0	1	0	1	0	0	1

Зашифроване значення дорівнює 41, що в ASCII є правою дужкою:)

Для розшифровки повідомлення використовуємо ключ і ту ж процедуру:

Зашифрований	0	1	0	1	0	0	1
Ключ	0	0	1	0	1	1	1
A	1	0	0	0	0	0	1

Будь-яка класична схема шифрування вразлива за двома пунктами:

• Якщо «погані хлопці» отримають ключ, вони теж можуть розшифрувати повідомлення. Так звані схеми шифрування відкритого ключа виявляють на відкритому каналі довгий рядок двійкових цифр, які повинні бути перетворені в ключ за допомогою секретної процедури; тут безпека заснована на обчислювальній складності «злому» секретної процедури.
• Оскільки у всіх повідомленнях є закономірності, такі як той факт, що переважає буква е, то якщо кілька повідомлень перехоплюються за допомогою одного і того ж ключа, погані хлопці можуть почати їх розшифрувати.

Щоб бути дійсно безпечним, значить, повинен бути унікальний секретний ключ для кожного повідомлення. Тому постає питання, як ми можемо генерувати унікальний ключ і бути впевненим, що погані хлопці не знають, що це таке.

Щоб надіслати ключ у квантовій криптографії, просто надішліть фотони в одній з чотирьох поляризацій: -45, 0, 45 або 90 градусів. Як відомо, приймач може виміряти, скажімо, поляризований фотон при 90 градусах, і якщо це не так, то будьте впевнені, чим він поляризувався при 0 градусах. Аналогічно приймач може виміряти, чи поляризувався фотон при 45 градусах, а якщо його немає, то він напевно поляризується при -45 градусах. Однак приймач не може виміряти як стан 0 градусів, так і стан 45 градусів, так як перше вимірювання руйнує інформацію другого, незалежно від того, який з них виконується першим.

Приймач вимірює вхідні фотони, випадковим чином вибираючи, чи слід вимірювати при 90 градусах або 45 градусах, і записує результати, але тримає їх у секреті. Одержувач зв'язується з відправником і повідомляє їй по відкритому каналу, який тип вимірювання був зроблений для кожного, не розкриваючи результату. Відправник повідомляє одержувачу, які з вимірювань були правильного типу. І відправник, і одержувач зберігають тільки кубіти, які були виміряні правильно, і вони тепер сформували ключ.

Якщо погані хлопці перехоплюють передачу фотонів, вимірюють їх поляризації, а потім відправляють їх на приймач, вони неминуче введуть помилки, оскільки не знають, яке вимірювання поляризації виконати. Два законних користувача квантового каналу перевіряють на підслуховування шляхом виявлення випадкової підмножини ключових бітів і перевірки частоти помилок на відкритому каналі. Хоча вони не можуть запобігти підслуховуванню, вони ніколи не будуть обдурені підслуховувачем, оскільки будь-які, якими б тонкими та витонченими зусиллями торкнутися каналу будуть виявлені. Всякий раз, коли вони не задоволені безпекою каналу, вони можуть спробувати знову налаштувати розподіл ключів.

До лютого 2000 року працююча система квантової криптографії за допомогою вищевказаної схеми досягла, за загальним визнанням, скромні швидкості 10 біт в секунду над довжиною 30 см.

Існує ще один метод квантової криптографії, який використовує заплутані фотони. Генерується послідовність корельованих пар частинок, причому по одному члену кожної пари виявляється кожна сторона (наприклад, пара фотонів, поляризації яких вимірюються сторонами). Підслуховувач на цьому зв'язку повинен був би виявити частинку, щоб зчитувати сигнал, і повторно передавати його, щоб його присутність залишалася невідомою. Однак акт виявлення однієї частинки пари руйнує її квантову кореляцію з іншою, і обидві сторони можуть легко перевірити, чи було це зроблено, не розкриваючи результатів власних вимірювань, шляхом зв'язку по відкритому каналу.