13.9: Квантові перешкоди

Last updated
Save as PDF

Page ID: 77208

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Повторний експеримент з подвійною щілиною

Пам'ятайте експеримент Янга з подвійною щілиною? Якби замість світлового променя ми направили пучок електронів у цю подвійну щілинну систему, що б ми побачили? Замінимо джерело світла на електронну піч, яка посилає потік електронів до подвійної щілинної системи; на хорошій відстані за подвійними щілинами лежить екран, який може фіксувати надходження кожного електрона. Припустимо, що налаштування було ретельно організовано так, що з електронів, які досягають екрана виявлення, рівно 50% з них надійшли з кожної щілини.

По-перше, ми помічаємо, що електрони - це справді точкові частинки; ті, які потрапляють через подвійну щілинну систему і досягають екрана виявлення, надходять в одне місце та одне місце лише на цьому екрані.

Якби ми закрили одну щілину і чекаємо деякий час, щоб дозволити великій кількості електронів досягти екрана виявлення, розподіл електронів виглядав би дещо так, як показано навпаки. Діаграма інтенсивності дещо розкинута, імовірно, тому, що частина електронів розсіяна від країв щілини. Зауважте, що, як і очікувалося, центр малюнка інтенсивності лежить у точці прямої видимості назад до електронної печі і трохи зміщений від точного центру екрана виявлення.

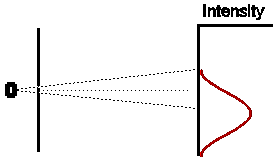
Аналогічним чином, якби ми закрили інший отвір і відкрили першу за ту ж кількість часу, ми б очікували (враховуючи, що наш експеримент був налаштований з точною симетрією), що малюнок інтенсивності буде ідентичний за формою до першого випадку, але зміщений рівну кількість на іншу сторону центр екрана виявлення.

Отже, якби обидві щілини були залишені відкритими на однакову кількість часу, що б ми очікували? Очевидно, що якби електрони були класичними частинками, ми очікуємо, що загальна картина інтенсивності - це просто сума двох попередніх моделей інтенсивності, показаних протилежно.

Дивно, але це зовсім не те, що ми спостерігаємо. Насправді спостережувана картина інтенсивності показує смуги перешкод, дуже схожі на ті, що виробляються світлом, що проходить через подвійну щілинну систему; на екрані виявлення є місця, де не приземляються електрони, та інші місця, де більше електронів, ніж число, яке ми очікували б від простого додавання вклади з кожної щілини діють поодинці.

Що відбувається??

Дивовижна річ полягає в тому, що електрони, які кожен надходять окремо як «частинки», роблять це таким чином, щоб сформувати схему інтенсивності, яку ми можемо мати сенс лише з точки зору «хвиль». Дійсно, використовуючи дуже просту теорію хвиль, яка дає опис експерименту з подвійною щілиною для хвиль, ми отримуємо повний опис всієї схеми інтенсивності цього подвійного щілинного експерименту для електронів. Щоб загнати точку додому, давайте розглянемо кілька модифікацій експерименту, які можуть допомогти розвіяти будь-які затяжні сумніви, що це дійсно те, що відбувається.

Ми можемо бути стурбовані тим, що якийсь ефект перешкод може відбуватися між різними електронами, коли вони проходять експериментальну систему. Щоб перевірити це, ми могли зменшити інтенсивність електронного пучка (наприклад, відключивши піч) так, щоб в будь-який момент в системі був лише один електрон. Надзвичайний результат полягає в тому, що, хоча для розвитку інтерференційної картини потрібно набагато більше часу, розвивається точно така ж картина.

Але як може кожен окремий електрон «знати», де він повинен приземлитися, так як експерименти говорять нам, що це залежить тільки від того, відкрита одна або обидві щілини. Так що, можливо, електрон якось розщеплюється і проходить через обидва отвори відразу, рекомбінуючись, перш ніж він досягне екрана виявлення. Щоб перевірити це, ми могли б спроектувати апарат, щоб перевірити, чи проходить електрон через одну щілину чи іншу, або обидві, коли обидві щілини відкриті.

Припустимо, що у нас є невелике світло, розміщене відразу за системою подвійних щілин. Він посилає фотони, щоб відскочити від електронів, що надходять через щілини; якщо електрон потрапив, він відхиляє фотони в наші очі, і ми спостерігаємо за електроном і можемо визначити його положення. (Звичайно, це дуже сира частина обладнання, щоб зробити таке вимірювання; насправді ми б спроектували речі набагато краще. Однак цей експеримент «gedanken» робить обговорення простішим, і являє собою основи реального експерименту). Тепер ми бачимо, через яку щілину проходить кожен електрон. Який результат? Виявляється, дійсно, кожен раз, коли електрон надходить через ту чи іншу щілину. Однак ми помічаємо до нашого занепокоєння, що коли ми робимо це спостереження, інтерференційна картина зникає!

Можливо, у нас так багато фотонів навколо, що вони якимось чином заважають шляхах електронів? Ну, ми можемо зменшити інтенсивність джерела світла (тобто кількість фотонів, що затоплюють систему), щоб перевірити це. Однак, якщо ми занадто сильно зменшимо інтенсивність, ми почнемо пропускати деякі електрони, тому що їх не вистачає навколо, щоб гарантувати, що кожен фотон вражений і, таким чином, спостерігається. Якщо ми подивимося на розподіл електронів, які ми пропускаємо, дійсно інтерференційна картина знову спостерігається. Однак для тих електронів, для яких ми можемо визначити, через яку щілину вони пройшли (і при виявленні вони завжди бачать, що вони проходять через ту чи іншу щілину!) , Ніякої інтерференційної картини не спостерігається.

Можливо, ми можемо припустити, що фотони, які ми використовуємо в цьому експерименті, занадто енергійні, так що їх вплив на тендітні електрони занадто велике. Ну, ми можемо зменшити їх вплив, зменшивши їх імпульс; оскільки їх довжина хвилі обернено пропорційна імпульсу, це означає, що ми збільшуємо їх довжину хвилі. І справді, коли ми збільшуємо довжину хвилі спостережуючих фотонів, ми починаємо

зверніть увагу, що інтерференційна картина відновлює себе. Однак, на наш страх, саме в цей момент ми виявляємо, що наша роздільна здатність (яка, пам'ятайте, пропорційна довжині хвилі спостережуваного світла) стала настільки поганою, що наша здатність визначати, через яку щілину пройшли ці електрони, зникає!

За словами Річарда Фейнмана (в «Характері фізичного права». (Преса MIT)):

«Якщо у вас є апарат, який здатний визначити, через який отвір проходить електрон... то ви можете сказати, що він або проходить через один отвір, або інший. Це робить; він завжди проходить через один отвір або інший - коли дивишся. Але коли у вас немає апарату, щоб визначити, через який отвір проходить річ, то ви не можете сказати, що вона проходить через один отвір чи інше... зробити висновок, що він проходить через один отвір чи інше, коли ви не шукаєте, - це зробити помилку в прогнозуванні. Це логічний канат, по якому ми повинні ходити, якщо хочемо інтерпретувати Природу».

Тепер можна подумати, що наша нездатність притиснути електрон до тієї чи іншої щілини одночасно, коли ми спостерігаємо інтерференційну картину, просто пов'язана з тим, що наше спостереження за системою занадто сильно порушує її. У цьому дійсно є частка правди; більшість сучасних вчених тепер визнають, що стара ідея про те, що спостерігач може стояти поза Природою, щоб спостерігати за нею, вже не є спроможною. Джон Уілер поставив це красиво, сказавши, що дійсно немає такого поняття, як «спостерігач» - тільки «учасники». Однак тут відбувається щось ще глибше: бо якби ми мали якийсь метод, щоб визначити, через яку щілину пройшов кожен електрон, проста логіка наполягала б на тому, що спостережуваний розподіл буде просто сумою розподілів електронів з кожної щілини, взятих окремо. Тобто ми повинні спостерігати

Тоді природа буде поміщена в нерозв'язний парадокс. Отже, мається на увазі, що майбутнє дійсно непередбачуване; ми ніколи не можемо передбачити, через яку щілину пройде електрон.

Принцип невизначеності Гейзенберга.

Існує більш формальне математичне твердження цього факту, яке називається Принцип невизначеності Гейзенберга, який встановлює чіткі обмеження на те, що ми можемо спостерігати. Просте «своєрідне доказ» йде наступним чином:

Розглянемо нашу спробу переглянути електрони в подвійній щілинній системі, сяючи на них світло довжини хвилі. Фотони цього світла матимуть momenta p фотон = h/. Якщо нам вдасться побачити електрон, це буде тому, що один з цих фотонів вразив його. Очевидно, що на імпульс електронів вплине ця взаємодія з фотоном. Назвемо зміни, які ми так індукували в імпульсі електрона p електрона (мається на увазі невелика зміна p електрона). Очевидно, що чим більше імпульс фотона, тим більше ця зміна імпульсу ураженого електрона. Звичайно р електрон пропорційний p фотону; константа пропорційності буде певною мірою залежати від експериментальної установки, але зазвичай може бути порядку 0,1 або близько того. Однак до порядку нашого нинішнього розрахунку ми можемо припустити, що він дорівнює 1. Таким чином, ми можемо записати, що р електрон = p фотон = h/.

Тепер ми знаємо, що точність, з якою ми можемо визначити відстань, обмежена розміром довжини хвилі світла, яку ми використовуємо для вимірювання відстані. Насправді ця невизначеність у положенні прямо пропорційна довжині хвилі світла; знову ж таки, на нашому нинішньому рівні точності, ми можемо встановити постійну пропорційності 1. У експерименті з подвійною щілиною назвемо цю невизначеність у позиції x. Отже, використовуючи наведені вище аргументи, ми можемо записати невизначеність в наших знаннях положення електрона, визначену світінням фотона довжини хвилі L на ньому, щоб бути x electron =. Поєднуючи два рівняння невизначеності імпульсу електрона та його положення, отримаємо наступний вираз для їх добутку: p електрон. х електрон = (h/) = h. Виявляється, цей вираз взагалі вірно для всіх частинок, і ми можемо записати його остаточно як р. х = ч. Це один із способів написання принципу невизначеності Гейзенберга.

Складність цього виведення Принципу невизначеності полягає в тому, що він може спонукати вас думати, що невизначеність в результаті, і справді пояснення всієї дивної поведінки, яку ми спостерігаємо в експерименті з подвійною щілиною, повністю пов'язана з неминучим порушенням, яке ми робимо, коли спостерігаємо. експеримент.

Однак це просто не відповідає дійсності. Принцип невизначеності передбачає вбудовану, неминучу межу точності, з якою ми можемо проводити вимірювання. NOR це схоже на експериментальну невизначеність, як це розуміється в класичній фізиці. Там, наприклад, коли ми хочемо виміряти температуру склянки води, це, безумовно, правда, що ми порушуємо температуру, яку хочемо виміряти, вводячи в неї холодний термометр, тому температура, яку ми вимірюємо, таким чином, не зовсім така, як у склянці поодинці. Однак, в принципі, ми можемо усунути цю помилку, вимірюючи з меншими та меншими термометрами та екстраполяцією на нульовий розмір; в принципі (якщо не на практиці) ми можемо таким чином виміряти довільно високу точність. Це неможливо в квантовому світі, завдяки принципу невизначеності Гейзенберга. Ще одним наслідком є те, що майбутнє не передбачуване в класичному розумінні; бо якщо ми точно не знаємо початкових умов - і принцип Гейзенберга говорить нам, що ми не можемо - ми не можемо робити точні прогнози про майбутнє, незалежно від того, наскільки точними та заздалегідь визначеними є наші рівняння.