13,8: Квантова заплутаність

Витоки цієї історії сягають корінням в самих початках квантової механіки в 1926 році. Насіннєвий папір був Ейнштейном, Подольським і Розеном в 1935 році, тому часто абревіатура ЕПР асоціюється з усім цим. На початку 1950-х Девід Бом повторно кинув аргумент ЕПР в більш чіткій формі, тому іноді абревіатура стає EPRB. У 1964 році Джон Белл опублікував теорему, яка зробила ситуацію ще зрозумілішою, тому іноді ми посилаємося на теорему Белла. Нарешті, вся історія заснована на парах об'єктів, які так чи інакше взаємопов'язані, навіть коли вони просторово розділені, і ми говоримо, що об'єкти заплутані.

Шкарпетки Бертльмана

Бертльманн, колега Белла в ЦЕРН, завжди носив невідповідні шкарпетки. Який колір він мав би на даній нозі в даний день, був досить непередбачуваним. Але коли ви бачите, що перший носок рожевий, ви можете бути впевнені, що другий носок не рожевий, навіть коли ви його не бачите. Малюнок, намальований Белом, ілюструє. Тут немає ніякої таємниці.

Важливе питання для носка: «Чи буде він прати?» Ми уявляємо організацію, що випробовує споживачів, яка хоче визначити, чи витримає носок прання, коли вода знаходиться при 0° C, або при 45° C, або при 90° C. Ми вважаємо, розумно, що прання знижується з підвищенням температури.

Ми уявляємо собі велику колекцію шкарпеток. Може спостерігатися варіативність їх змиваемости. Ми випадковим чином ділимо колекцію на третини, і припускаємо, що у нас досить велика колекція, щоб пральна здатність шкарпеток однаково представлена в кожній третій. Ми стираємо одну колекцію шкарпеток при 0°, а ті, що витримують, ми стираємо при 45°. Другу колекцію шкарпеток ми стираємо при 45°, а ті, що витримують, миємо при 90°. Третю колекцію ми миємо при 0°, а ті, що виживають, миємо при 90°. Так як пральна здатність кожної колекції шкарпеток однакова:

Число, яке виживає при 0°, а не при 45° Plus

Число, яке виживає при 45°, а не при 90°, не менше

Число, яке виживає при 0°, а не при 90°

Таємниці тут теж немає. Для кожного члена третьої групи або він не вижив би при 45° і був би в першій групі, або він вижив би при 45° і був би у другій групі.

Але шкарпетки Бертльмана бувають парами. Ми припускаємо, що кожна окрема пара шкарпеток має різні кольори, але однакові можливості прання. Тоді, якщо ми протестуємо велику вибірку пар його шкарпеток, співвідношення внизу попередньої сторінки стане:

Кількість пар, в яких одна виживає при 0°, а інша не при 45° плюс

Кількість пар, в яких одна виживає при 45°, а інша не при 90°, не менше

Кількість пар, в яких одна виживає при 0°, а інша не при 90°

Електрон Спін

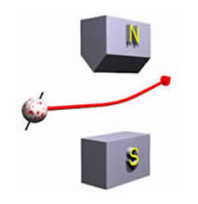Коли заряджений класичний об'єкт обертається, якщо ми кидаємо його між полюсами дивного магніту, він буде відхилений або вгору, або вниз. Величина прогину залежить від:

• Загальний заряд на об'єкт і його розподіл.
• Швидкість і орієнтація віджиму

Якщо взяти пучок електронів з електронної гармати і запустити його через магніт, ми побачимо щось дивне: всі електрони відхиляються вгору на якусь фіксовану величину або відхиляються вниз на точно таку ж величину, і яка для кожного окремого електрона здається випадковим. Якщо відхилення вгору, ми говоримо, що електрон «обертається вгору», і якщо він відхилений вниз, ми говоримо, що це «спина вниз».

Є речовини, які виділяють електрони попарно. Кожен електрон діє так само, як електрони з електронної гармати. Але коли ми дивимося на пари електронів, ми бачимо, що якщо один електрон «обертається», то його супутником є «спина вниз» і навпаки. Тож ми можемо назвати ці електрони Бертльмана: якщо виміряти один і побачити, що він обертається, ви знаєте, що його супутник не обертається, він обертається вниз. Фізики часто говорять, що ці пари мають загальний спін нуль і що два електрони заплутані.

Те, що електрони можуть мати тільки два спінових стану - загадка. Справа в тому, що електрони Бертльмана мають сумарний спін нуль, немає.

Існує ще одна таємниця про електрони, або з електронної гармати, або однієї з пар Бертльмана: якщо я обертаю магніт, скажімо, на 45° або 90° навколо осі початкового шляху електронів, я отримую той же результат, що і раніше: всі електрони відхиляються вгору на деяку фіксовану величину або відхиляються вниз точно така ж кількість, і яка для кожного окремого електрона видається випадковою. Відзначимо, що визначення «вгору» визначається орієнтацією магніту.

Ми можемо розширити дослідження пральної здатності пар шкарпеток на заплутані пари електронів з однією тривіальною різницею. Для шкарпеток, якщо хтось пережив прання при 45°, ми припускали, що інший член пари теж. Для електронів Бертльмана, якщо хтось обертається на 45°, його супутник обертається вниз на 45°, тобто його супутник не спін-вгору на 45°. Отже, тепер відношення у верхній частині попередньої сторінки стає:

Кількість пар, для яких одна обертається на 0°, а інша - спін-вгору для 45° Plus

Кількість пар, для яких одна спін-ап на 45°, а інша - спін-вгору на 90°, не менше

Кількість пар, для яких одна спін-вгору на 0°, а інша - віджимання на 90°

Це співвідношення було експериментально перевірено, і не відповідає дійсності! Отже, очевидно, існує певна різниця між шкарпетками Бертльмана та електронами Бертльмана, і ми зробили принаймні одне неправильне припущення десь у отриманні цього співвідношення для електронів.

Виявляється, фактичний експериментальний результат прогнозується квантовою механікою, тому які б неправильні припущення ми не зробили, також порушуються цією теорією.

Припущення

Ми використали певну логіку при отриманні співвідношення шкарпеток та електронів Бертльмана. Ми також зробили два припущення при виведенні відносин. Обидва настільки очевидні, що легко пропустити той факт, що ми їх взагалі зробили.

По-перше, коли ми говорили про кількість шкарпеток або електронів при 0° та 90°, ми припускали, що кожен пройде або не пройде тест при 45°. Іншим чином, ми припускали існування миючої здатності при деякій температурі або віджимання під деяким кутом, навіть якщо це насправді не було виміряно. Якщо говорити ще іншим способом, ми припустили, що існує реальність, незалежна від її спостереження. Це схоже на стару філософську пилку про дерево, що падає в лісі: якщо ні у кого не було звуку?

По-друге, коли ми говоримо про вимірювання миючої здатності або віджиму одного члена пари, щоб визначити щось про його супутника, ми припускали, що оскільки ми проводили одночасні вимірювання двох різних шкарпетків/електронів в різних місцях, ефект одного вимірювання не може порушити результат вимір іншого члена пари. Іншим способом ми припустили, що жоден сигнал або вплив не можуть поширюватися нескінченно швидко. Іноді це припущення називають місцевістю.

Таким експериментальним шляхом ми довели, що принаймні одне з цих двох припущень є неправильним для заплутаних електронів.

Так що?

Експериментальні випробування довели, що немає реальності окремо від її спостереження та/або різні частини Всесвіту миттєво пов'язані з кожною іншою частиною Всесвіту. Тож ми дізналися щось глибоке про фізичний світ.

Ніхто не замислювався глибше про всесвіт, який не існує незалежно від його спостереження, ніж Джон Арчибальд Уілер. Він запропонував нам викинути слово «спостерігач» зі свого словника, замінивши його на «учасник». Малюнок нижче був придуманий ним. Він коментує цифру:

Символічне зображення Всесвіту як самозбудженої системи, що виникла за допомогою «самовідліку». Всесвіт народжує спілкуються учасників. Спілкуються учасники надають сенсу Всесвіту... З такою концепцією йде нескінченна серія відступаючих відображень, які можна побачити в парі звернених дзеркал.

Девід Бом глибоко думав про всесвіт, який миттєво пов'язаний з кожною іншою частиною Всесвіту. Він припустив, що в основі нашого повсякденного Всесвіту, який він назвав експлікаційним порядком, існує основний порядок, причетний, в якому немає поділу в просторі чи часі. Фігура - аналогія, розроблена Бомом.

Ми можемо дивитися тільки на екрани телевізорів, і ми бачимо двох риб в різних місцях. Як ми продовжуємо дивитися, ми починаємо помічати кореляцію між рухами двох риб. Це тому, що в основі реальності двох екранів лежить одна єдність, одна риба, яку ми можемо спостерігати лише з двох різних точок зору.

Таким чином, ця заплутаність бізнесу викликає деякі глибокі роздуми про природу світу. Прагматик може сказати «Так що?» Так само в середині дев'ятнадцятого століття Фарадей, Максвелл і інші замислювалися про природу електрики і магнетизму. Британський прем'єр-міністр Гладстон, як повідомляється, запитав Фарадея, яку можливу користь можуть мати такі пусті спекуляції. Фарадей відповів: «Одного дня, сер, ви будете це оподатковувати».

Заплутаність майже напевно має практичне застосування, яке, імовірно, в кінцевому підсумку буде оподатковуватися. До них відносяться квантові комп'ютери, які можуть мати на порядок більшу потужність, ніж будь-який звичайний комп'ютер може досягти, і квантова телепортація ala транспортер в Star Trek. Розробка цих додатків є «червоним гарячим» полем досліджень і розробок.

Дізнатися більше

Луїза Гілдер, Епоха заплутаності: коли відроджувалася квантова фізика.

Читання цієї книги змусило мене привезти Луїзу до Торонто на колоквіум з фізики в січні. Фотографія була зроблена на колоквіумі. Колоквіум у свою чергу призвів до запрошення для мене виступити з цією промовою. Книга доступна в твердій обкладинці, м'якій обкладинці та на Kindle.

Джон Белл, «Шкарпетки Бертльмана і природа реальності» (1980)

Перші кілька розділів мого маленького документа майже плагіатують1 з класичного паперу Белла. Його можна легко знайти через Google.

Девід Мермін, «Квантові таємниці для будь-кого» (J. Філософія 78, стор. 397, 1981) та «Принесення додому атомного світу: квантові таємниці для кого» (Amer. Фізика 49, стор. 940, 1981).

Ці майже однакові папери блискучі. Перша версія мала великий вплив на Луїзу Гілдер. Я підготував флеш-анімацію на основі паперів Мерміна:

http://faraday.physics.utoronto.ca/P...in/Mermin.html

Девід Бом, Цілісність і причетний порядок (1980).

У цій книзі обговорюється мислення Бома про нелокальний всесвіт.

Девід Гаррісон, «Теорема Белла» (1999, остання редакція 2006).

Тривала дискусія з деякою схожістю з цим документом. Він доступний за адресою:

http://www.upscale.utoronto.ca/PVB/H...lsTheorem.html

Я вражений і задоволений тим, що теорема Гуглінга Белла перераховує цей документ 2-й, відразу після запису у Вікіпедії.