5.2: Рішення

Малюнок 5.1: Зміна хвильової функції в області III, для найнижчого стану, у міру збільшення глибини потенційної ями. Ми використали a = 1 0− 1 0 м, і k 0 a= 2, 3, 4, 5, 6, 7, 8, 9 і 1 0.

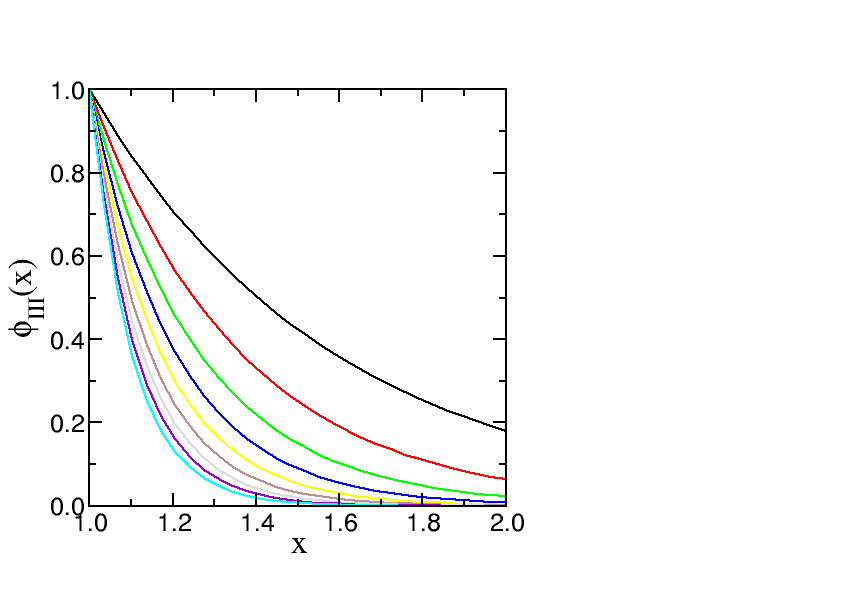
Як було зазначено раніше, аргументи неперервності для похідної хвильової функції не застосовуються для нескінченного стрибка потенційної енергії. Це легко зрозуміти, коли ми дивимося на поведінку рішення з низькою енергією в одному з двох зовнішніх регіонів (I або III). У цьому випадку хвильова функція може бути наближена як

\[e ± k r\]

з\(k = 2 m ℏ^ 2 V 0\)

який зменшується до нуля швидше і швидше, коли V 0 стає все більшим і більшим. Зрештою хвильова функція більше не може проникати в область нескінченної потенційної енергії. Неперервність хвильової функції тепер означає, що (a) =( − a) = 0.

Визначення

\[κ = \sqrt{ 2 m ℏ^ 2 E}\]

ми виявляємо, що існує два типи розв'язків, які задовольняють граничній умові:

\[ϕ 2 n + 1 ( x ) = \cos ( κ 2 n + 1 x )\]

\[ ϕ 2 n ( x ) = \sin ( κ 2 n x ) .\]

Тут

\[κ l = π l 2 a .\]

Таким чином, ми маємо ряд власних станів\ (l (x), l= 1,, ∞). Енергії є

\[E_l = ℏ^2 π^2 l 2 8 a^2.\]

Малюнок 5.2: Кілька хвильових функцій нескінченної квадратної свердловини.

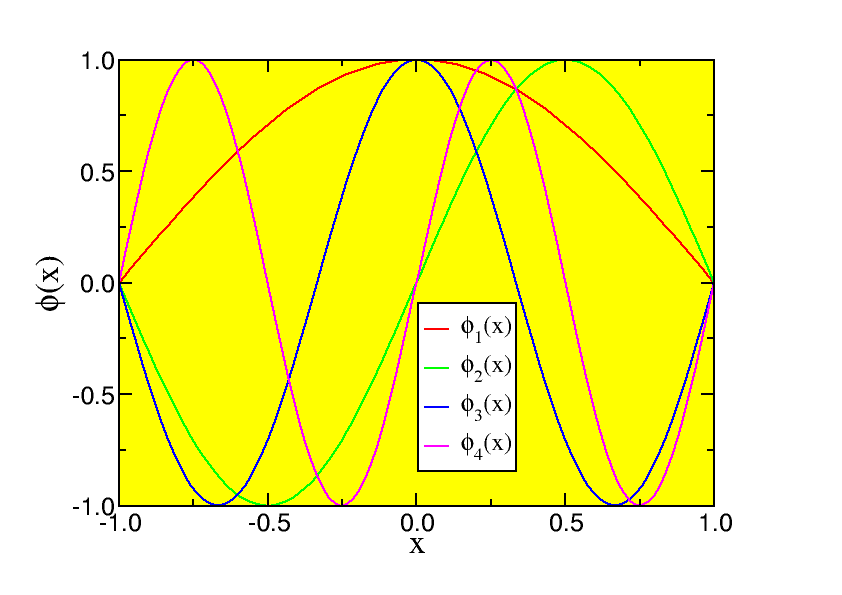
Ці хвильові функції дуже добре ілюструють ідею нормалізації. Дозвольте мені подивитися на нормалізацію наземного стану (найнижчого стану), що

\[ϕ 0 ( x ) = A 1 \cos π x 2 a\]

for − a< x< a та 0 в інших місцях.

Нам потрібно вимагати

\ − ∞ ∞ | 0 (x) | 2 д х = 1,\]

де потрібно розглянути абсолютне значення, так як A 1 може бути комплексним. Нам потрібно лише інтегрувати від − a до a, оскільки решта інтеграла дорівнює нулю, і ми маємо

\[∫ − ∞ ∞ | ϕ 0 ( x ) | 2 d x = | A | 2 ∫ − a a cos 2 π x 2 a d x = | A | 2 2 a π ∫ − π ∕ 2 π ∕ 2 cos 2 y d y = | A | 2 2 a π ∫ − π ∕ 2 π ∕ 2 1 2 ( 1 + cos 2 y ) d y = | A | 2 2 a π π . \]

Тут ми змінили змінні з x на\ (y=π x^2 a). Таким чином, робимо висновок, що вибір

\[A = 1 2 a\]

призводить до нормалізації хвильової функції.