Skip to main content
LibreTexts - Ukrayinska

2.8: Інтенсивність

  1. Last updated
  2. Save as PDF
  • Page ID
    77344

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Інтенсивність джерела в заданому напрямку - це потужність, випромінювана на одиницю твердого кута близько заданого напрямку, тобто.

    \[ I = dP/d \omega.\]

    Одиниці СІ є ват на один стерадіан (W sr -1). Інтенсивність елемента площі є добутком його сяйва та проектованої площі., А інтенсивність поверхні в заданому напрямку є інтегралом сяйва над проектованою площею поверхні. Як приклад, форму астероїда неправильної форми можна наблизити як сукупність з'єднаних плоских трикутних граней; дві такі грані показані на малюнку 1.

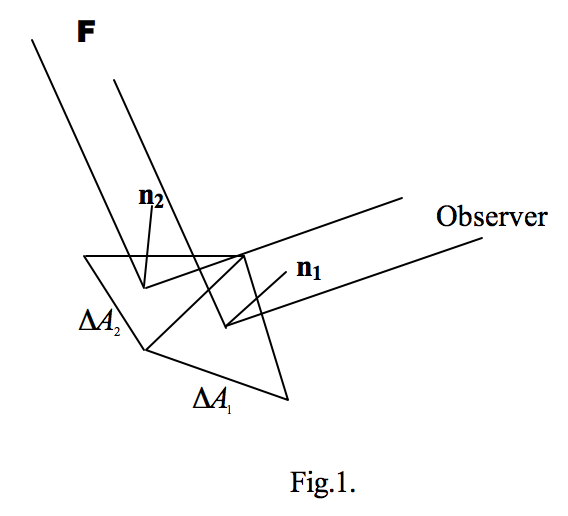
    Знімок екрана 2019-07-12 в 4.35.52 PM.png

    Для кожної грані площі Δ A k внесок в інтенсивність у напрямку спостерігача дорівнює.

    \[ \Delta I_k = L_{obs, k} \Delta A_k \cos \theta_k\]

    де θ k - кут між поверхневим вектором нормалі n k і (фіксованим) напрямком до спостерігача. Загальна інтенсивність (у напрямку до спостерігача) астероїда тоді

    \[ I = \sum_{k = 1}^{N} \Delta A_k\]

    де N - загальна кількість граней, як опромінених, так і видимих спостерігачеві.

    Особливий інтерес представляє інтенсивність сфери як функція сонячного фазового кута α. Якщо розглядати сферу радіуса α, центровану в рамці O xyz, зі спрямованими сферичними координатами (θ, Φ), опромінену з х -напрямку з щільністю потоку F, елемент площі поверхні дорівнює α 2 sin θ Dθ Dφ, а його проектована площа у напрямку μ дорівнює μα 2 син θ dθ dφ.

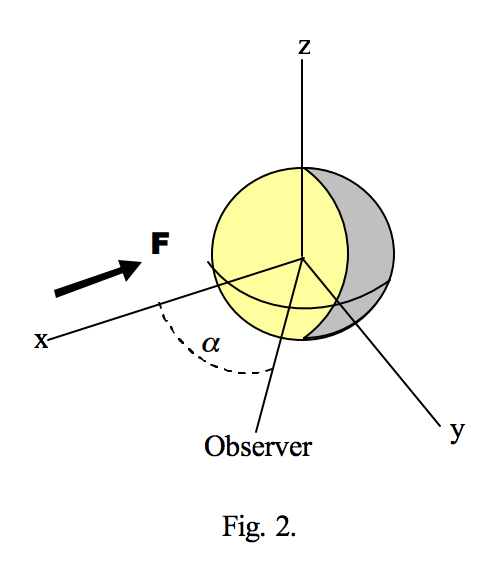
    Знімок екрана 2019-07-12 в 4.41.25 PM.png

    Опромінення точки (α, θ, Φ) точки на поверхні E = F μ 0, де може бути показано, що

    \[ \mu_0 = \sin \Theta \cos \Phi,\]

    і для спостерігача при фазовому куті α в xy -площині

    \[ \mu = \sin \Theta \cos ( \alpha - \Phi ), \]

    в цьому випадку інтенсивність як функція фазового кута задається

    \[ I ( \alpha) = \alpha^2 \textbf{F} \int_{ \alpha - \pi/2}^{ \pi/2} \int_0^{ \pi} f_r \mu_0 \mu \sin \Theta d \Theta d \Phi.\]

    Ми повернемося до цього рівняння, докладніше, в §9.