Skip to main content
LibreTexts - Ukrayinska

13.16: Топоцентрично-геоцентрична корекція

  1. Last updated
  2. Save as PDF
  • Page ID
    77928

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    У розділі 13.1 я вказав дві невеликі (але не мізерно малі) поправки, які необхідно було зробити, а саме\(∆T\) корекцію (яку можна зробити на самому початку розрахунку) і корекцію на світловий час, яку можна зробити, як тільки будуть визначені геоцентричні відстані — після чого необхідно перерахувати геоцентричні відстані від початку! Я насправді не вносив ці виправлення в нашому числовому прикладі, але я вказав, як їх зробити.

    Є ще одна невелика корекція, яку потрібно зробити. Діаметр Землі зменшує кут\(17".6\) at\(1 \ \text{au}\), тому спостережуване положення астероїда помітно залежить від того, звідки він спостерігається на поверхні Землі. Спостереження, звичайно, повідомляються як топоцентричні — тобто з місця (\(τοπος\)), де знаходився спостерігач. Вони повинні бути виправлені комп'ютером до геоцентричних положень - але, звичайно, це не може бути зроблено, поки відстані не будуть відомі. Як тільки відстані відомі, можна зробити світловий час і топоцентрично-геоцентричні поправки. Тоді, звичайно, потрібно повернутися до початку і перерахувати відстані - можливо, більше одного разу, поки не буде досягнуто конвергенції. У цьому розділі показано, як зробити топоцентрично-геоцентричну корекцію.

    Ми використовували позначення\(\mathfrak{x, y , z}\) для геоцентричних координат, і я буду використовувати\(\mathfrak{x^\prime , \ y^\prime , \ z^\prime}\) для топоцентричних координат. На малюнку\(\text{XIII.3}\) я показую Землю з точки в екваторіальній площині, а зверху північного полюса. Радіус Землі дорівнює\(R\), а радіус невеликого кола широти\(\phi\) (де знаходиться спостерігач) дорівнює\(R \cos \phi\). The\(\mathfrak{x}\) - і\(\mathfrak{x}^\prime -\) осі спрямовані в бік першої точки Овна,\(\Upsilon\).

    З малюнка повинно бути видно, що поправки даються

    \[\mathfrak{x}^\prime = \mathfrak{x} - R \cos \phi \cos \text{LST}, \label{13.16.1} \tag{13.16.1}\]

    \[\mathfrak{y}^\prime = \mathfrak{y} - R \cos \phi \sin \text{LST} \label{13.16.2} \tag{13.16.2}\]

    і\[\mathfrak{z}^\prime = \mathfrak{z} - R \sin \phi . \label{13.16.3} \tag{13.16.3}\]

    Будь-якому спостерігачеві, який подає спостереження в Центр малої планети, присвоюється код обсерваторії, тризначне число. Цей код не тільки ідентифікує спостерігача, але, пов'язаний з Кодексом обсерваторії, Центр Малої Планети веде облік величин\(R \cos \phi\) і\(R \sin \phi\) в\(\text{AU}\). Ці величини, в позначеннях, що використовуються на\(\text{MPC}\), позначаються як\(−∆_{xy}\) і\(−∆_{z}\) відповідно. Вони унікальні для кожного місця спостереження.

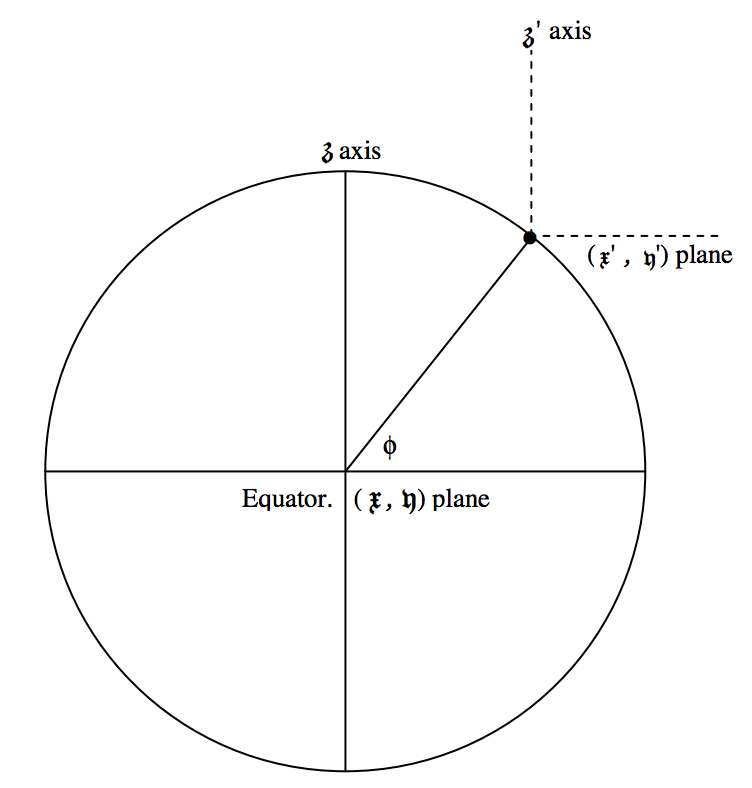
    Малюнок 13.3 copy.png

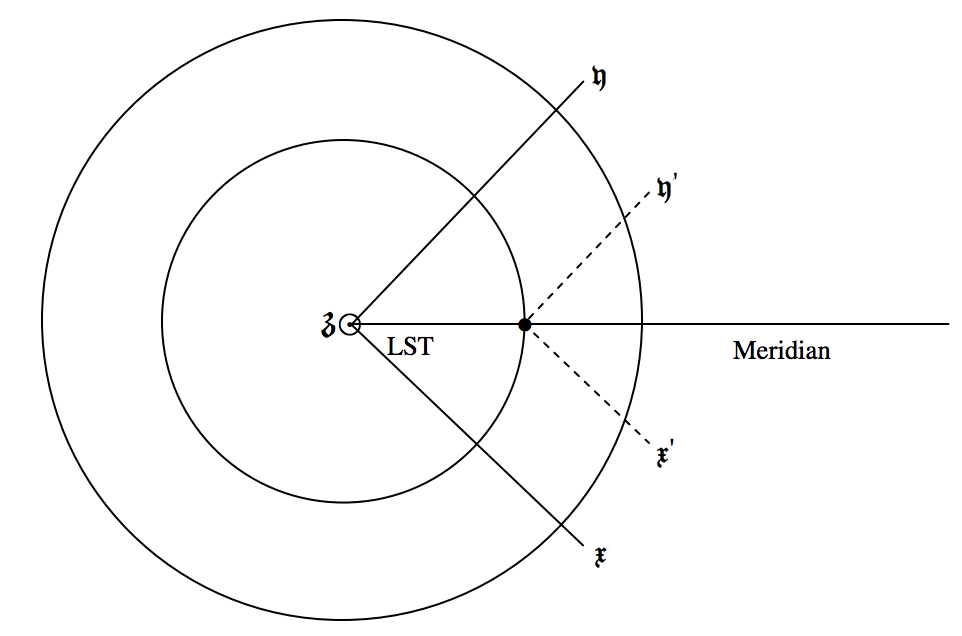
    Малюнок 13.3.1 copy.png
    \(\text{FIGURE XIII.3}\)