5.6: Ефект доплера

Last updated
Save as PDF

Page ID: 78286

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Цілі навчання

До кінця цього розділу ви зможете:

Поясніть, чому спектральні лінії фотонів, які ми спостерігаємо від об'єкта, змінюватимуться в результаті руху об'єкта до нас або від нас
Опишіть, як можна використовувати ефект Доплера, щоб вивести, як астрономічні об'єкти рухаються через простір

Останні два розділи познайомили вас з багатьма новими поняттями, і ми сподіваємось, що через них ви побачили одну головну ідею. Астрономи можуть дізнатися про елементи в зірках і галактиках шляхом розшифровки інформації в їх спектральних лініях. Однак існує ускладнюючий фактор у навчанні декодувати повідомлення зоряного світла. Якщо зірка рухається до нас або від нас, її лінії будуть в дещо іншому місці в спектрі від того, де вони були б у зірці в спокої. І більшість об'єктів у Всесвіті дійсно мають певний рух відносно Сонця.

Рух впливає на хвилі

У 1842 році Крістіан Доплер вперше виміряв вплив руху на хвилі, найнявши групу музикантів, щоб грати на відкритому залізничному вагоні, коли він рухався вздовж колії. Потім він застосував те, що навчився, до всіх хвиль, включаючи світло, і зазначив, що якщо джерело світла наближається або відступає від спостерігача, світлові хвилі будуть, відповідно, переповнені тісніше один до одного або розкинуті. Загальний принцип, відомий зараз як ефект Допплера, проілюстрований на малюнку\(\PageIndex{1}\).

альт — Малюнок\(\PageIndex{1}\): Ефект доплера. (a) Джерело, S, робить хвилі, чиї пронумеровані гребені (1, 2, 3 і 4) омивають над стаціонарним спостерігачем. (b) Джерело S тепер рухається до спостерігача A і подалі від спостерігача C. Хвильовий гребінь 1 був випущений, коли джерело знаходився в положенні S4, гребінь 2 в позиції S2, і так далі. Спостерігач А бачить хвилі, стиснуті цим рухом, і бачить синій зрушення (якщо хвилі легкі). Спостерігач C бачить хвилі, витягнуті рухом, і бачить червоне зсув. Спостерігач B, чия лінія зору перпендикулярна руху джерела, не бачить зміни хвиль (і відчуває себе залишеним).

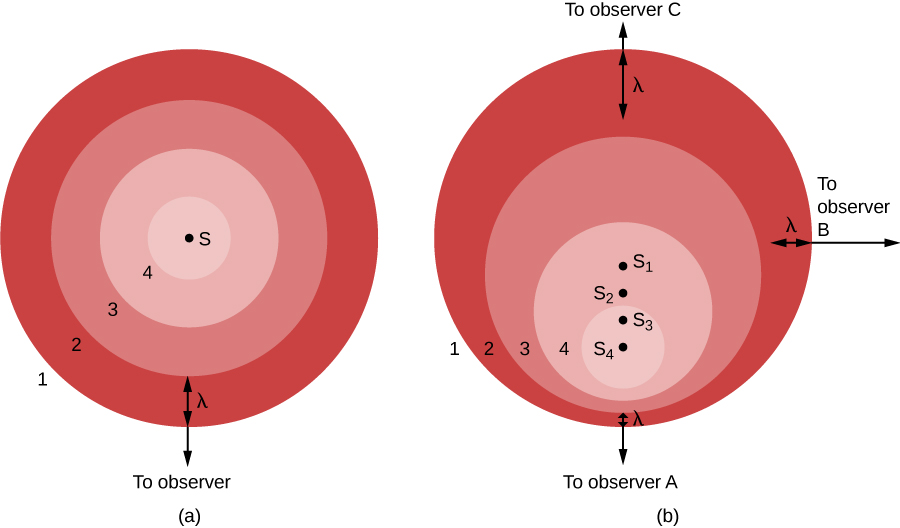
На\(\PageIndex{1a}\) малюнку джерело світла (S) знаходиться в спокої щодо спостерігача. Джерело видає ряд хвиль, гребені яких ми позначили 1, 2, 3 і 4. Світлові хвилі розподіляються рівномірно у всіх напрямках, як брижі від сплеску у водоймі. Гребені розділені відстанню, λ, де λ - довжина хвилі. Спостерігач, який виявляється розташований у напрямку нижньої частини зображення, бачить світлові хвилі, що йдуть красиво і рівномірно, одна довжина хвилі один від одного. Спостерігачі, розташовані в іншому місці, побачать те ж саме.

З іншого боку, якщо джерело світла рухається по відношенню до спостерігача, як видно на малюнку\(\PageIndex{1b}\), ситуація складніша. Між тим часом, коли один гребінь випромінюється, а наступний готовий вийти, джерело трохи перемістився, до нижньої частини сторінки. З точки зору спостерігача А, цей рух джерела зменшив відстань між гребенями - це стискання гребенів разом, може сказати цей спостерігач.

На малюнку\(\PageIndex{1b}\) ми показуємо ситуацію з точки зору трьох спостерігачів. Джерело видно в чотирьох положеннях,\(S_1\),\(S_2\)\(S_3\), і\(S_4\), кожна з яких відповідає випромінюванню одного гребеня хвилі. Спостерігач А, хвилі, здається, слідують один за одним більш уважно, при зменшеній довжині хвилі і, таким чином, збільшеній частоті. (Пам'ятайте, всі світлові хвилі рухаються зі швидкістю світла через порожній простір, незважаючи ні на що. Це означає, що рух не може впливати на швидкість, а лише на довжину хвилі та частоту. У міру зменшення довжини хвилі частота повинна збільшуватися. Якщо хвилі будуть коротшими, більше зможе рухатися повз протягом кожної секунди.)

Ситуація не така для інших спостерігачів. Давайте розглянемо ситуацію з точки зору спостерігача С, розташованого навпроти спостерігача А на малюнку\(\PageIndex{1}\). Для неї джерело віддаляється від свого місця розташування. В результаті хвилі не стискаються разом, а натомість поширюються рухом джерела. Гребені надходять зі збільшеною довжиною хвилі і зниженою частотою. До спостерігача Б, в напрямку під прямим кутом до руху джерела ніякого ефекту не спостерігається. Довжина хвилі і частота залишаються такими ж, як вони були в частині (а) фігури.

З цієї ілюстрації видно, що ефект Допплера створюється лише рухом до спостерігача або від нього, рух називається радіальною швидкістю. Боковий рух такого ефекту не виробляє. Спостерігачі між А і В спостерігали б деяке скорочення світлових хвиль для тієї частини руху джерела, яка знаходиться уздовж їх прямої видимості. Спостерігачі між B і C спостерігали б подовження світлових хвиль, які знаходяться уздовж їх прямої видимості.

Можливо, ви чули ефект Допплера зі звуковими хвилями. Коли до вас наближається свисток поїзда або поліцейська сирена, а потім віддаляється, ви помітите зменшення висоти тону (саме так людські почуття інтерпретують частоту звукових хвиль) звукових хвиль. Порівняно з хвилями в спокої, вони змінилися від трохи більш частих при наближенні до вас, до трохи менш частих, коли віддаляєтеся від вас.

Приємний приклад такої зміни звучання свистка поїзда можна почути в кінці класичної пісні Beach Boys «Caroline, No» на їх альбомі Pet Sounds. Щоб почути цей звук, перейдіть до цієї версії пісні YouTube. Звук поїзда починається приблизно о 2:20.

Кольорові зрушення

Коли джерело хвиль рухається до вас, довжина хвилі трохи зменшується. Якщо задіяні хвилі є видимим світлом, то кольори світла трохи змінюються. Коли довжина хвилі зменшується, вони зміщуються до синього кінця спектра: астрономи називають це синім зрушенням (оскільки кінець спектра дійсно фіолетовий, термін, ймовірно, повинен бути фіолетовим зсувом, але синій - більш поширений колір). Коли джерело віддаляється від вас і довжина хвилі стає довшою, ми називаємо зміну кольорів червоним зсувом. Оскільки ефект Допплера вперше був використаний з видимим світлом в астрономії, терміни «blueshift» і «redshift» стали добре усталеними. Сьогодні астрономи використовують ці слова для опису змін довжин хвиль радіохвиль або рентгенівських променів так само зручно, як вони використовують їх для опису змін у видимому світлі.

Чим більше рух у напрямку або від нас, тим більший доплерівський зсув. Якщо відносний рух повністю йде уздовж прямої видимості, формула доплерівського зсуву світла дорівнює

\[\dfrac{\Delta λ}{λ}= \frac{v}{c} \nonumber\]

де\(\lambda\) - довжина хвилі, що випромінюється джерелом,\(\Delta \lambda\) - різниця між\(\lambda\) і довжиною хвилі,\(c\) виміряна спостерігачем,\(v\) це швидкість світла, і відносна швидкість спостерігача і джерела в прямому видимості. Змінна\(v\) вважається позитивною, якщо швидкість є спадом, і негативною, якщо вона є одним із підходів. Вирішуючи це рівняння для швидкості, знаходимо

\[ v = c \times \dfrac{\Delta \lambda}{\lambda}. \nonumber\]

Якщо зірка наближається або відступає від нас, довжини хвиль світла в її безперервному спектрі здаються скороченими або подовженими відповідно, як і темні лінії. Однак, якщо його швидкість не становить десятки тисяч кілометрів в секунду, зірка не здається помітно синішою або червонішою, ніж зазвичай. Таким чином, доплерівський зсув не легко виявляється в безперервному спектрі і не може бути точно виміряний в такому спектрі. Однак довжини хвиль ліній поглинання можна точно виміряти, і їх доплерівський зсув відносно просто виявити.

Приклад\(\PageIndex{1}\): Ефект Допплера

Ми можемо використовувати рівняння ефекту Доплера для обчислення радіальної швидкості об'єкта, якщо ми знаємо три речі: швидкість світла, вихідну (незміщену) довжину хвилі випромінюваного світла та різницю між довжиною хвилі випромінюваного світла та довжиною хвилі, яку ми спостерігаємо. Для конкретних ліній поглинання або випромінювання ми зазвичай точно знаємо, яку довжину хвилі має лінія в наших лабораторіях на Землі, де джерело світла не рухається. Ми можемо виміряти нову довжину хвилі за допомогою наших приладів у телескопі, і тому ми знаємо різницю в довжині хвилі через доплерівське зсув. Оскільки швидкість світла є універсальною константою, то ми можемо обчислити радіальну швидкість зірки.

Особлива емісійна лінія водню спочатку випромінюється з довжиною хвилі 656,3 нм з газової хмари. У нашому телескопі ми спостерігаємо, що довжина хвилі лінії випромінювання повинна бути 656,6 нм. Як швидко ця газова хмара рухається до Землі або подалі від неї?

Рішення

Оскільки світло зміщується на довшу довжину хвилі (червоне зміщення), ми знаємо, що ця газова хмара віддаляється від нас. Швидкість можна розрахувати за формулою доплерівського зсуву:

\[ν=c×\dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left( \dfrac{0.3 ~ \text{nm}}{656.3 ~ \text{nm}} \right)= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.3 \times 10^{–9} ~ \text{m}}{656.3 \times 10^{–9} ~ \text{m}} \right)=140,000 ~ \text{m/s} =140 ~ \text{km/s} \nonumber\]

Вправа\(\PageIndex{1}\)

Припустимо, спектральна лінія водню, в нормі при 500 нм, спостерігається в спектрі зірки на рівні 500.1 нм. Як швидко зірка рухається до Землі або від неї?

Відповідь

Оскільки світло зміщується на довшу довжину хвилі, зірка віддаляється від нас:

\[ν=c \times \dfrac{\Delta \lambda}{\lambda}= \left(3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 ~ \text{nm}}{500 ~ \text{nm}} \right)=\left( 3.0 \times 10^8 ~ \text{m/s} \right) \left(\dfrac{0.1 \times 10^{–9} ~ \text{m}}{500 \times 10^{–9} ~ \text{m}} \right)=60,000 ~ \text{m/s}\]

Його швидкість становить 60 000 м/с.

Тепер ви можете запитати: якщо всі зірки рухаються, а рух змінює довжину хвилі кожної спектральної лінії, чи не стане це катастрофою для астрономів, які намагаються з'ясувати, які елементи присутні в зірках? Зрештою, саме точна довжина хвилі (або колір) говорить астрономам, які лінії належать до якого елемента. І ми спочатку вимірюємо ці довжини хвиль у контейнерах з газом у наших лабораторіях, які не рухаються. Якщо кожна лінія в спектрі зірки тепер зміщена своїм рухом на іншу довжину хвилі (колір), як ми можемо бути впевнені, які лінії і які елементи ми дивимося в зірці, швидкість якої ми не знаємо?

Візьміть серце. Ця ситуація звучить гірше, ніж є насправді. Астрономи рідко судять про наявність елемента в астрономічному об'єкті по одній лінії. Саме візерунок ліній, унікальний для водню або кальцію, дозволяє нам визначити, що ці елементи є частиною зірки чи галактики, яку ми спостерігаємо. Ефект Допплера не змінює візерунок ліній від заданого елемента - він лише трохи зміщує весь візерунок у бік червонішої або синьої довжини хвиль. Зміщений візерунок все ще досить легко розпізнати. Найкраще, коли ми розпізнаємо звичний шаблон елемента, ми отримуємо бонус: сума, на яку зсувається візерунок, може дати нам можливість визначити швидкість об'єктів у нашій прямої видимості.

Навчання астрономів включає в себе велику роботу по навчанню декодування світла (і іншого електромагнітного випромінювання). Умілий «декодер» може дізнатися температуру зірки, які елементи в ній знаходяться, і навіть її швидкість в напрямку до нас або від нас. Це дійсно вражаюча кількість інформації для зірок, які знаходяться на відстані світлових років.

Резюме

Якщо атом рухається до нас, коли електрон змінює орбіти і виробляє спектральну лінію, ми бачимо, що лінія трохи зміщена до синього кольору своєї нормальної довжини хвилі в спектрі. Якщо атом віддаляється, ми бачимо лінію, зміщену до червоного. Цей зсув відомий як ефект Доплера і може бути використаний для вимірювання радіальних швидкостей віддалених об'єктів.

Глосарій

Допплерівський ефект: видима зміна довжини хвилі або частоти випромінювання від джерела через його відносного руху від або до спостерігача

радіальна швидкість: рух у напрямку або від спостерігача; складова відносної швидкості, яка лежить у прямому видимості