Skip to main content
LibreTexts - Ukrayinska

3: Експоненціальна інтегральна функція

  1. Last updated
  2. Save as PDF
  • Page ID
    77737

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Рано чи пізно (зокрема в наступному розділі) при вивченні зоряних атмосфер нам потрібна експоненціальна інтегральна функція. Цей короткий розділ не містить нічого про зоряні атмосфери або навіть астрономії, але він описує стільки, скільки нам потрібно знати про експоненціальну інтегральну функцію. Він не призначений як ретельне виклад всього, що можна було б написати про функцію.

    Експоненціальна інтегральна функція порядку\(n\), записана як функція змінної\(a\), визначається як

    \[E_n(a) = \int_1^\infty x^{-n} e^{-ax} dx. \label{3.1}\]

    Я обмежуся випадками, коли\(n\) є невід'ємним цілим числом і\(a\) є невід'ємною дійсною змінною. Для теорії зоряної атмосфери в наступному розділі нам буде потрібно\(n\) до 3 включно.

    Почнемо з того, що побачимо, які значення функцій коли\(a = 0\). У нас є

    \[E_n (0) = \int_1^\infty x^{-n} dx \label{3.2}\]

    і це нескінченно для\(n = 0\) і для\(n = 1\). Для більшого\(n\) він є\(1/(n − 1)\).

    Таким чином\(E_0(0) = \infty\)\(E_1 (0) = \infty\),\(E_2 (0) = 1\),,\(E_3(0) = \frac{1}{2}\)\(E_4(0) = \frac{1}{3}\), і т.д.

    Після цього функції (будь-якого порядку) монотонно зменшуються зі\(a\) збільшенням, наближаючись до нуля асимптотично для великих\(a\).

    \(E_0(a)\)Функцію легко оцінити. Це

    \[E_0(a) = \int_1^\infty e^{-ax} dx = \frac{e^{-a}}{a}. \label{3.3}\]

    Оцінка експоненціальної інтегральної функції для менш проста, але\(n > 0\) це може бути зроблено за допомогою числової (наприклад, Сімпсона) інтеграції. Верхня межа інтеграла в рівнянні 3.1 нескінченна, але цю складність можна подолати за допомогою підстановки\(y = 1/x\), з якої рівняння стає

    \[E_n(0) = \int_0^1 y^{n-2} e^{-a/y} dy. \label{3.4}\]

    Оскільки обидві межі є кінцевими, це тепер в принципі може бути інтегровано чисельно простим способом, наприклад, правилом Сімпсона або подібним алгоритмом, за винятком того, що на нижній межі\(a/y\) нескінченно, і спочатку необхідно визначити межу integrand as\(y → 0\), яка дорівнює нулю.

    Існує, однак, спосіб оцінки експоненціальної інтегральної функції\(n ≥ 2\) без необхідності чисельного інтегрування. Розглянемо, наприклад,

    \[E_{n+1}(a) = \int_1^\infty x^{-(n+1)} e^{-ax} dx. \label{3.5}\]

    Якщо це інтегровано (дуже обережно!) по частинам, ми приходимо до

    \[E_{n+1}(a) = \frac{1}{n} \left[ e^{-a} - aE_n (a) \right]. \label{3.6}\]

    Таким чином, з цього відношення повторення, як тільки ми оцінили\(E_1(a)\), ми можемо оцінити\(E_2(a)\) і, отже,\(E_3(a)\) і так далі.

    Відношення повторення\(\ref{3.6}\), однак, тримається лише для\(n ≥ 1\) (як стане очевидним під час ретельної часткової інтеграції), тому немає можливості обійти числове інтегрування для\(n = 1\). Крім того, для малих значень\(a\) функцій для\(n = 0\) або\(1\) стають дуже великими, стають нескінченними як\(a → 0\), що робить їх дуже чутливими при спробі обчислити наступну функцію вгору. Таким чином, для малого\(a\) або для побудови таблиці може в кінцевому підсумку бути менше проблем взяти бика за роги і інтегрувати їх усіх чисельно.

    Це дозволить собі хорошу практику програмування, щоб підготувати таблицю\(E_n(a)\) для\(a = 0\)\(2\), в кроках\(0.01\), для\(n = 0, 1, 2, 3\). Таблиця в ідеалі повинна мати п'ять стовпців, перший -\(201\) значення\(a\), а решта чотири\(E_n(a)\) -\(n = 1\) до\(4\). Графік цих функцій показаний на малюнку\(\text{III.1}\).

    На практиці, виконуючи розрахунки по фігурі\(\text{III.1}\), це те, що я знайшов. Функція для\(n = 0\) була легкою; вона задається просто рівнянням\(\ref{3.3}\). Для\(n = 1\), я інтегрований за правилом Сімпсона;\(100\)\(y\) інтервали в були достатніми для обчислення функції до дев'яти знаків після коми. Функція для\(n = 2\) була несподівано складною. Відношення повторення не\(\ref{3.6}\) було корисним в малих\(a\) випадках, як обговорювалося вище. Тому я спробував інтегрувати його за допомогою правила Сімпсона, але, хоча функція, на перший погляд, дуже проста:

    \[E_2(a) = \int_0^1 e^{-a/y} dy, \label{3.7} \]

    Правило Сімпсона здавалося неадекватним для обчислення функції точно навіть з такою кількістю\(1000\) інтервалів в\(y\). Ні рекуррентне відношення, ні числове інтегрування не було без проблем! У мене не було ніяких труднощів, однак, з інтеграцією функції з\(n = 3\), і тому я потім використовував повторення відношення назад, щоб обчислити функцію для\(n = 2\) і все було добре.

    альт
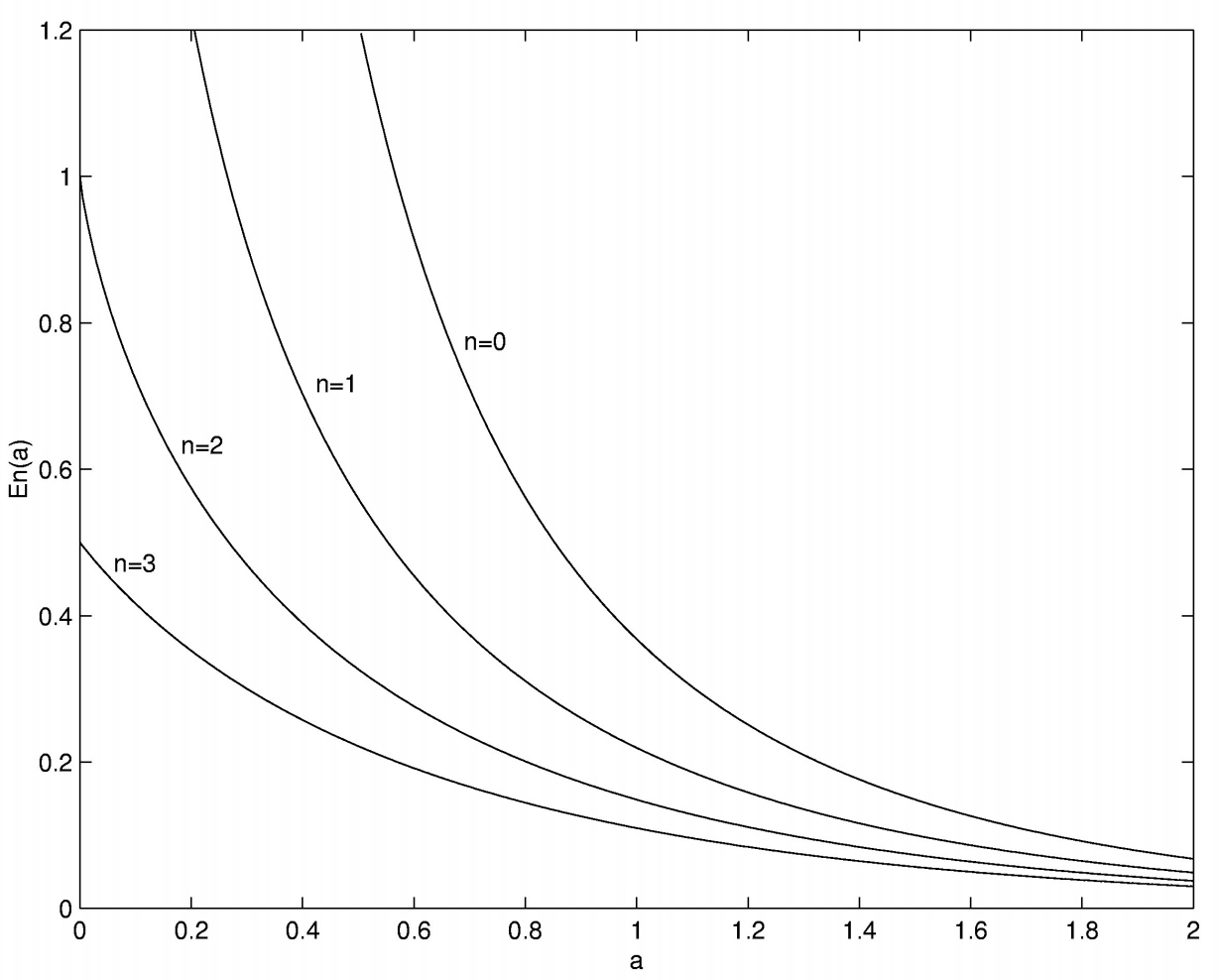
    \(\text{FIGURE III.1}\)
    Експоненціальна інтегральна функція