13.7: Принцип Франка-Кондона

Принцип Франка-Кондона описує інтенсивності вібронічних переходів, або поглинання або випромінювання фотона. Він стверджує, що коли молекула зазнає електронний перехід, такий як іонізація, ядерна конфігурація молекули не зазнає значних змін. Це пов'язано з тим, що ядра набагато масивніше електронів і електронний перехід відбувається швидше, ніж можуть реагувати ядра. Коли ядро перебудовується з новою електронною конфігурацією, теорія стверджує, що воно повинно зазнати вібрації.

Якщо уявити вертикальний перехід від наземного до збудженого електронного стану як відбувається з коливальної хвильової функції, що дає розподіл ймовірностей знаходження ядер у заданій області простору, то можна визначити ймовірність заданого коливального рівня з інтеграла перекриття,$S_{v’,v}$ який. дає перекриття коливальної хвильової функції в грунті і збудженому стані. $v’$Квантові числа відносяться до основного стану, а$v$ квантові числа відносяться до збудженого стану. Імовірність переходу може бути розділена на електронну та ядерну частини за допомогою наближення Кондона.

Рисунок Template:index: Енергетична діаграма Франка — Кондона. Оскільки електронні переходи дуже швидкі в порівнянні з ядерними рухами, вібраційні рівні сприятливі, коли вони відповідають мінімальній зміні ядерних координат. Показані потенційні свердловини, що сприяють переходам між$v = 0$ and $v' = 2$. ( CC-SA-BY-3.0; Samoza).

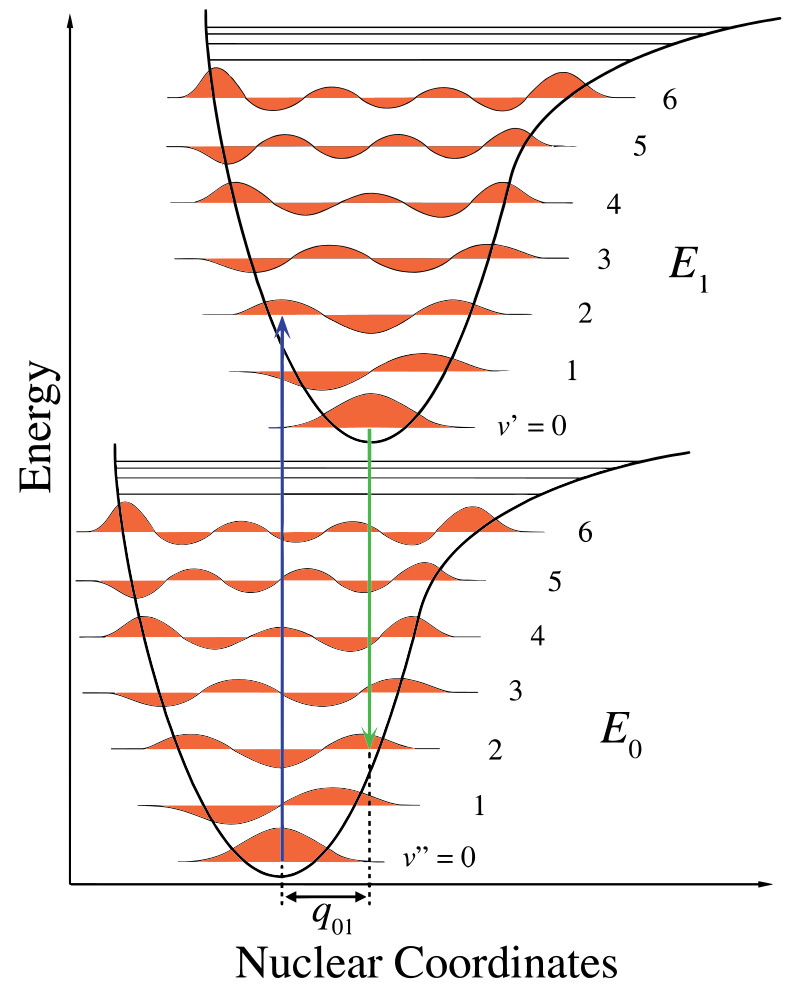
На малюнку Template:index ядерна вісь показує наслідок міжядерного поділу, а вібронічний перехід позначається синьою та зеленою вертикальними стрілками. Ця цифра демонструє три речі:

1. Поглинання призводить до більш високого енергетичного стану,
2. флуоресценція призводить до більш низького енергетичного стану, і
3. зсув ядерних координат між землею і збудженим станом свідчить про нове положення рівноваги потенціалу ядерної взаємодії. Той факт, що стрілка флуоресценції коротше поглинання, вказує на те, що у неї менше енергії, або що довжина хвилі її довша.

Класичне наближення Кондона

Апроксимація Кондона - це припущення, що електронний перехід відбувається за короткою шкалою часу порівняно з ядерним рухом, так що ймовірність переходу може бути розрахована при фіксованому ядерному положенні.

Ця зміна вібрації зберігається під час стану, що називається швидким електронним збудженням. Отримані кулонівські сили виробляють рівновагу, як показано на малюнку для ядер, які називаються поворотною точкою. Поворотну точку можна зіставити, провівши вертикальну лінію від мінімуму нижньої кривої до перетину вищого електронного стану. Ця процедура називається вертикальним переходом і обговорювалася раніше в контексті фотоелектронної спектроскопії (інша електронна спектроскопія).

Принцип Франка-Кондона пояснює відносні інтенсивності вібронічних переходів, пов'язуючи ймовірність коливального переходу з перекриттям коливальних хвильових функцій. Він стверджує, що ймовірність виникнення коливального переходу зважується інтегралом перекриття Франка-Кондона:

$$P_{i \rightarrow f} = | \langle \psi^*_{final} | \boldsymbol{\mu} | \psi_{initial} \rangle | ^2 = | \int \psi^*_{final} \boldsymbol{\mu} \psi_{initial} d\tau | ^2 \nonumber$$

У межах наближення Франка-Кондона ядра вважаються «фіксованими» під час електронних переходів. Таким чином, електронні переходи можна вважати вертикальними переходами на електронних кривих потенційної енергії (вієричні переходи на рисунку Template:index).

Квантовий принцип Франка-Кондона

Принцип Франка-Кондона має як класичне, так і квантове застосування. Класично принцип Франка-Кондона - це наближення того, що електронний перехід, швидше за все, відбудеться без змін положень ядер у молекулярній сутності та її середовищі. Отриманий стан називається державою Франка-Кондона, а перехід, який бере участь, вертикальним переходом. Квантова механічна формулювання цього принципу полягає в тому, що інтенсивність вібронічного переходу пропорційна квадрату інтеграла перекриття між коливальними хвильовими функціями двох станів, які беруть участь в переході.

Принцип Франка-Кондона заснований на наближенні Борна-Оппенгеймера, що дозволяє розділити електронні$q$ та ядерні$Q$ хвильові функції з урахуванням загальної хвильової функції.

$$| \psi_{total}(Q,q) = | \psi_{nuc}(Q) \rangle \psi_{el} (Q;q) \rangle \nonumber$$

Оскільки оператор переходу,$\hat{\mu}(q)$, залежить тільки від електронної складової, то ядерні компоненти можуть бути відокремлені від інтеграла перехідного моменту, який диктує ймовірність виникнення переходу:

$$\begin{align} \langle \psi^{*}_{total, f} | \hat{\mu} | \psi_{total, i} \rangle &= \langle \psi^*_{nuc, f} | \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle | \psi_{nuc, i} \rangle \\[4pt] &= \underbrace{ \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle}_{\text{nuclear overlap}} \langle \psi^{*}_{el, f} | {\boldsymbol{\mu}} | \psi_{el, i} \rangle \end{align} \nonumber$$

Якщо інтеграл ядерного перекриття дорівнює нулю для цього переходу, то перехід спостерігатися не буде, незалежно від величини електронного фактора.

$S_{00}$Перехід оцінюється в моделі гармонічного осцилятора

Ядерне перекриття для переходу нуль-нуль$S_{00}$ можна обчислити досить просто, використовуючи визначення гаусової форми хвильових функцій гармонічного осцилятора.

Хвильова функція нульової точки в наземному електронному стані дорівнює

$$| \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber$$

Хвильова функція нульової точки в збудженому електронному стані дорівнює

$$| \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber$$

де

• $\alpha = \dfrac{\sqrt{mk}}{\hbar}$
• $R_e$- рівноважна довжина зв'язку в наземному електронному стані
• $Q_e$довжина рівноважної зв'язку в збудженому електронному стані

Інтеграл ядерного перекриття є

$$S_{00}= \langle \psi^*_{nuc, f} | \psi_{nuc, i} \rangle = \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(R-R_e)^2/2} e ^{-\alpha(R-Q_e)^2/2} dR \label{FC1}$$

Показник у рівнянні$\ref{FC1}$ можна розширити як

$$S_{00}= \sqrt{\dfrac{\alpha}{\pi}} \int_{\infty}^{\infty} e ^{-\alpha(2R^2-RR_e - 2RQ_e+ R^2_e + Q_e^2)/2} dR \label{FC2}$$

і ми використовуємо

$$(R_e + Q_e)^2 = R_e^2 + Q_e^2 + 2R_eQ_e \nonumber$$

і

$$(R_e - Q_e)^2 = R_e^2 + Q_e^2 - 2R_eQ_e \nonumber$$

підставити і завершити квадрат всередині інтеграла. Ми можемо висловити

$$R_e^2 + Q_e^2 = \dfrac{1}{2}[(R_e + Q_e)^2 + (R_e - Q_e)^2]. \nonumber$$

Таким чином, інтеграл у рівнянні$\ref{FC2}$ є

$$S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \int_{-\infty}^{\infty} e ^{-\alpha\{R- 1/2(R_e+Q_e)\}^2} dR \nonumber$$

Інтеграл є гауссовим інтегралом. Ви можете показати, що якщо ми дозволимо,$z = \sqrt{\alpha}\{R-1/2(R_e + Q_e)\}$ то$dz = \sqrt{\alpha} dR$ і інтеграл стає

$$S_{00}= \sqrt{\dfrac{\alpha}{\pi}} e^{-\alpha(R_e -Q_e)^2/4} \dfrac{1}{\sqrt{\alpha}} \int_{-\infty}^{\infty} e^{z^2} dz \label{FC3}$$

цей інтеграл вже вирішено, з таблиці інтегралів, Рівняння$\ref{FC3}$ стає

$$S_{00} = e^{-\alpha(R_e-Q_e)^2/4} \nonumber$$

Ми б дотримувалися тієї ж процедури, щоб розрахувати, що перекриття нульового рівня вібрації в землі до першого збудженого коливального рівня збудженого стану:$S_{01}$.

$S_{01}$Перехід оцінюється в моделі гармонічного осцилятора

Для обчислення перекриття нульового рівня ґрунтового стану ($v=0$) з першим рівнем збудженого стану ($v'=1$) ми використовуємо поліном Ерміта$H_1(x) =2x$ для опису хвильової функції збудженого стану (див. тут огляд хвильових функцій гармонічного осцилятора). Ось$x = \sqrt{\alpha}(R - Q_e)$.

$$S_{01}= \langle \psi^{*}_{nuc, f} | \psi_{nuc, i} \rangle \label{FC01}$$

з нульовою точкою хвильової функції в наземному електронному стані

$$| \psi(R) \rangle = \big| \left(\dfrac{\alpha}{\pi} \right)^{1/4} e ^{-\alpha(R-R_e)^2/2} \big\rangle \nonumber$$

Першою хвилевою функцією збудженого стану в збудженому електронному стані є

$$| \psi(R) \rangle = \big | \left(\dfrac{\alpha}{\pi} \right)^{1/4} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \big\rangle \nonumber$$

Потім перекриття нульового рівня стану землі з першим рівнем збудженого стану (рівняння$\ref{FC01}$)

$$S_{01} = \dfrac{1}{\sqrt{2}} \sqrt{\dfrac{\alpha}{\pi}} \int_{-\infty}^{\infty} e^{-\alpha(R-R_e)^2/2} \sqrt{\alpha}2 (R-Q_e) e^{-\alpha(R-Q_e)^2/2} \nonumber$$

і

$$S_{01} = \sqrt{\dfrac{2 \alpha^2}{\pi}} e^{-\alpha(R_e-Q_e)^2/4} \int_{-\infty}^{\infty} (R-Q_e) e^{-\alpha \{R- 1/2 (R_e+Q_e)^2\}} \nonumber$$

Такі ж заміни можуть бути зроблені, як і вище, так що інтеграл може бути записаний як (не показаний і бути продемонстрований в домашніх вправах) і кінцевий результат

$$S_{01} = \sqrt{\dfrac{\alpha^2}{2}} (R_e-Q_e) e^{-\alpha(R_e-Q_e)^2/4} \nonumber$$

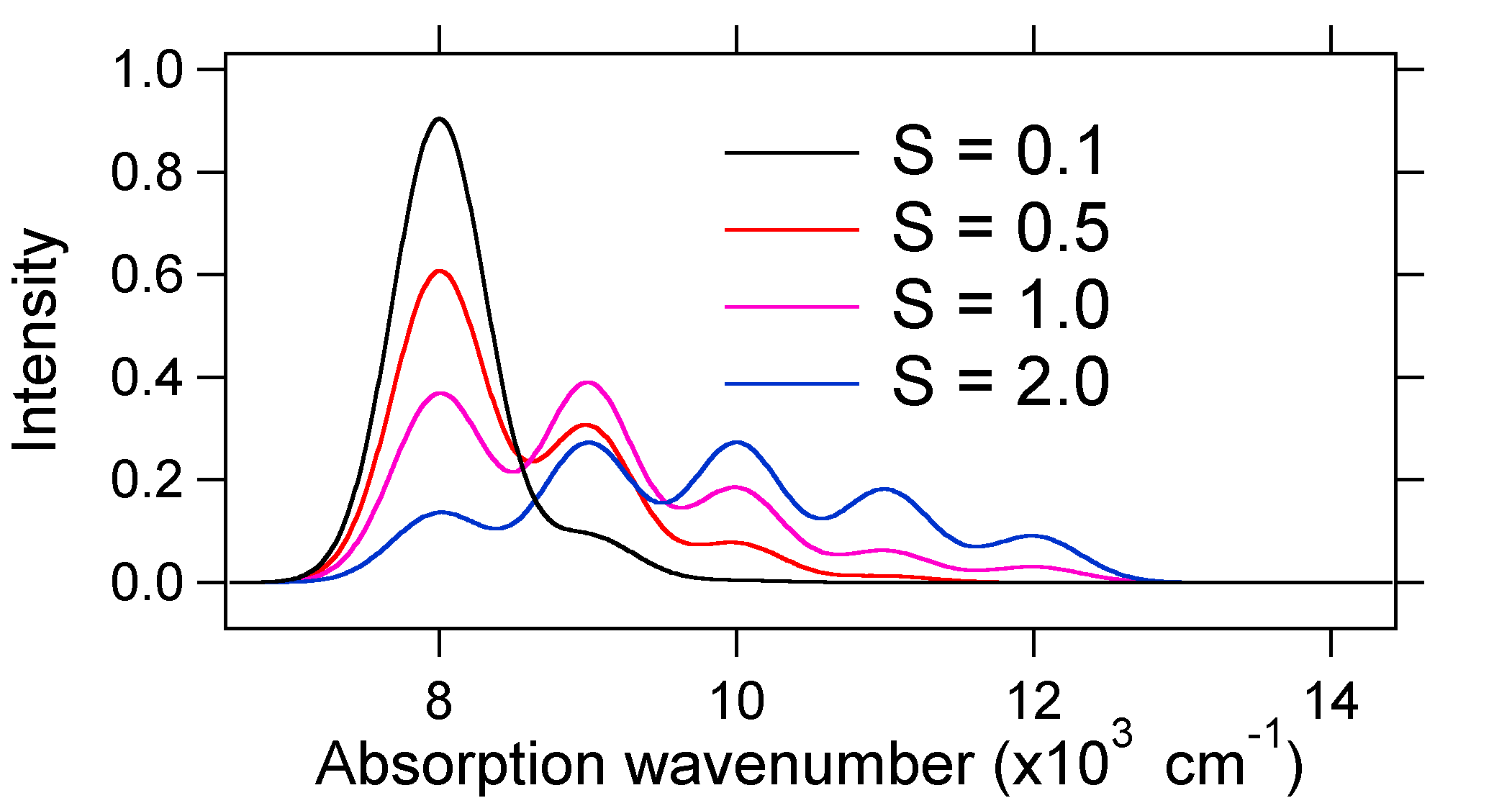
Ми могли б продовжити і обчислити, що перекриття нульового рівня в наземному стані з усіма вищими коливальними рівнями світла:$S_{02}$$S_{03}$, і т.д. кожен термін відповідає переходу з різною енергією, оскільки коливальні рівні мають різні енергії. Потім смуга поглинання має вигляд прогресії (прогресія Франка-Кондона) переходів між різними рівнями кожен зі своєю ймовірністю.

Франк-Кондон прогресії

Щоб зрозуміти значення наведеної вище формули для коефіцієнта ФК, дослідимо ґрунтовий і збуджений стан потенційної енергетичної поверхні при$T = 0$ Кельвіні. Нижче наведено два стани, розділені енергією 8000 см ^-1. Це поділ енергії між днищами їх потенційних свердловин, а також між відповідними рівнями енергії з нульовою точкою. Припустимо, що хвильове число коливального режиму дорівнює 1 000 см ^-1 і що довжина зв'язку збільшується за рахунок того, що електрон видаляється з орбіти зв'язку і поміщається в антисклеювальную орбіталь при електронному збудженні.

Рисунок Template:index: Переходи хвилевих функцій для системи моделей гармонійних осциляторів з помірним зміщенням (S=1).

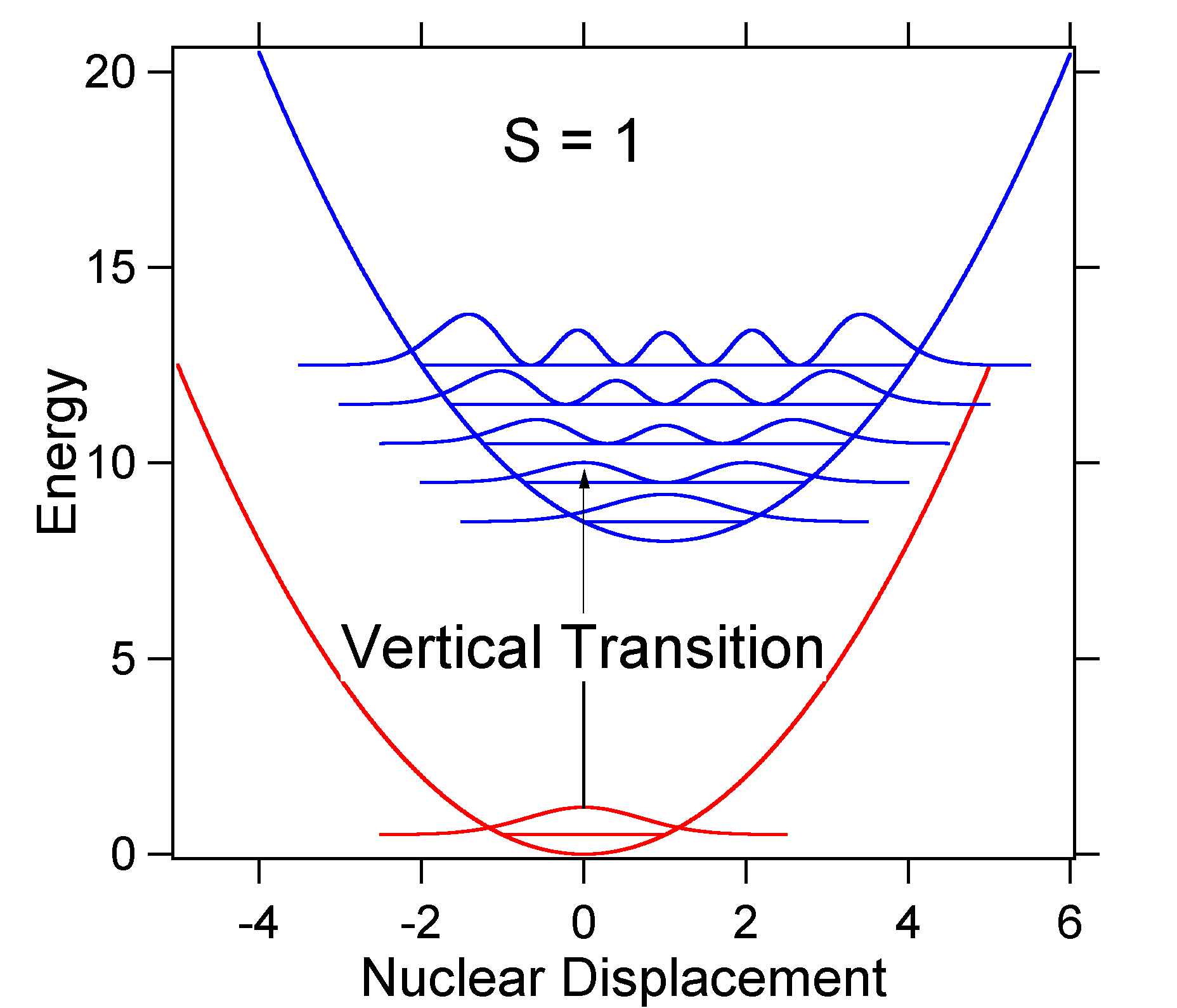
Відповідно до наведеної вище моделі для фактора Франка-Кондона ми створили б спектр «палиці» (рис. Template:index), де кожен коливальний перехід нескінченно вузький і перехід може відбуватися лише тоді, коли$E = h\nu$ саме. Наприклад, поверхні потенційної енергії були задані для S = 1, а ймовірність переходу на кожному рівні задається палицями (чорними) на малюнку нижче.

Рисунок Template:index: Спектр палиці, одягнений гаусами, для системи гармонічних осциляторів помірного зміщення (S=1) з Figure Template:index.

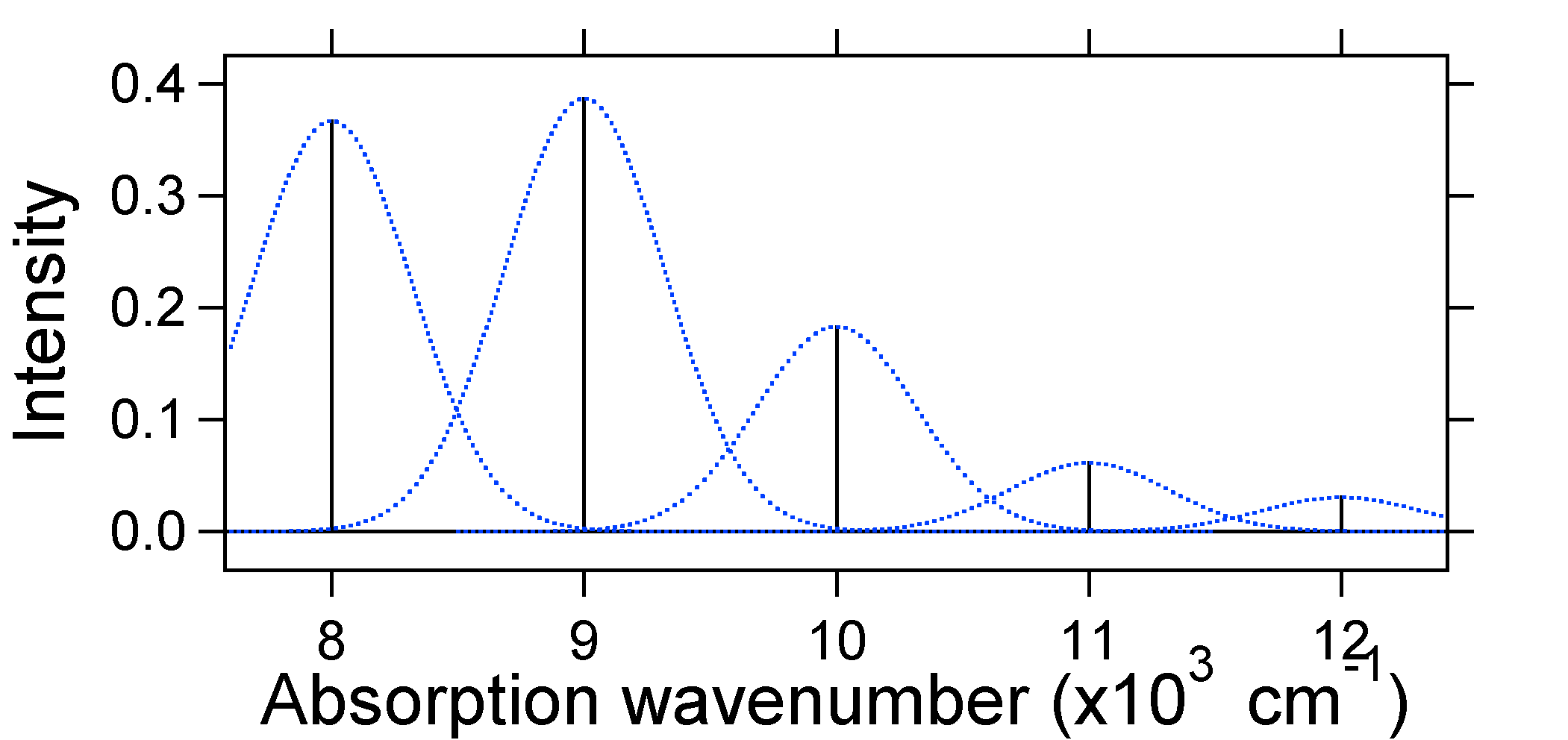
Пунктирні гауси, які оточують кожну палицю, дають більш реалістичну картину того, як повинен виглядати спектр поглинання. В першу чергу кожному енергетичному рівню (палиці) буде надаватися деяку ширину за рахунок того, що стан має кінцевий термін служби. Таке розширення називається однорідним розширенням, оскільки воно впливає на всі молекули в ансамблі аналогічним чином. Відбувається також розширення через невеликі відмінності в середовищі кожної молекули. Такий вид уширення називається неоднорідним розширенням. Незалежно від походження, модель вище була створена за допомогою гаусового розширення.

Ядерне зміщення між землею і збудженим станом визначає форму спектра поглинання. Розглянемо як менший, так і великий збуджений стан зміщення. Якщо$S = ½$ і потенційні енергетичні поверхні в цьому випадку є:

Рисунок Template:index: Переходи хвилевих функцій для системи моделей гармонійних осциляторів з малим зміщенням (S=1/2).

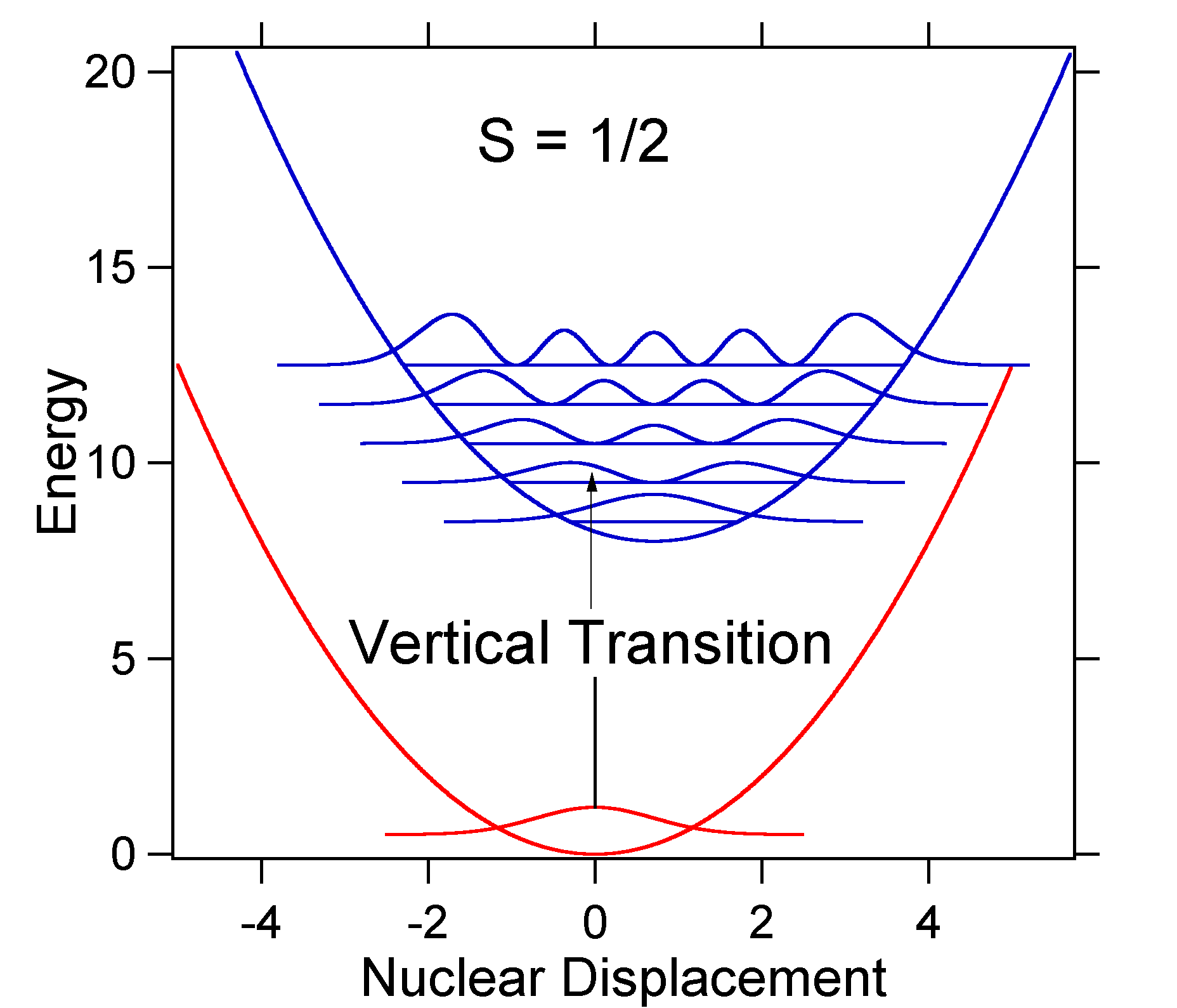
У цьому випадку спектр «палиці» має вигляд на рисунку Template:index

Рисунок Template:index: Спектр палиці, одягнений гаусами, для системи гармонічних осциляторів малого зміщення (S = 1/2) з рисунка Template:index.

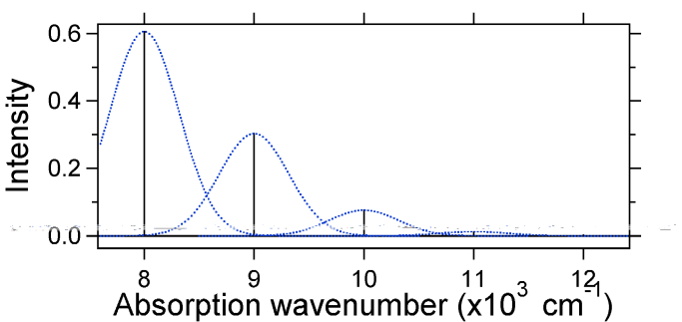
Зверніть увагу, що нуль-нуль або$S_{0,0}$ коливальний перехід набагато великий в тому випадку, коли зміщення невелике.

Як правило,$S$ константа дає відношення інтенсивності$v = 2$ переходу до$v = 1$ переходу. У цьому випадку з$S = 0.5$,$v=2$ перехід дорівнює 0,5 інтенсивності$v=1$ переходу.

Як приклад більшого зміщення, розташування поверхонь потенційної енергії для S = 2 показано нижче.

Рисунок Template:index: Переходи хвилевих функцій для системи моделей гармонійних осциляторів з сильним зміщенням (S=2).

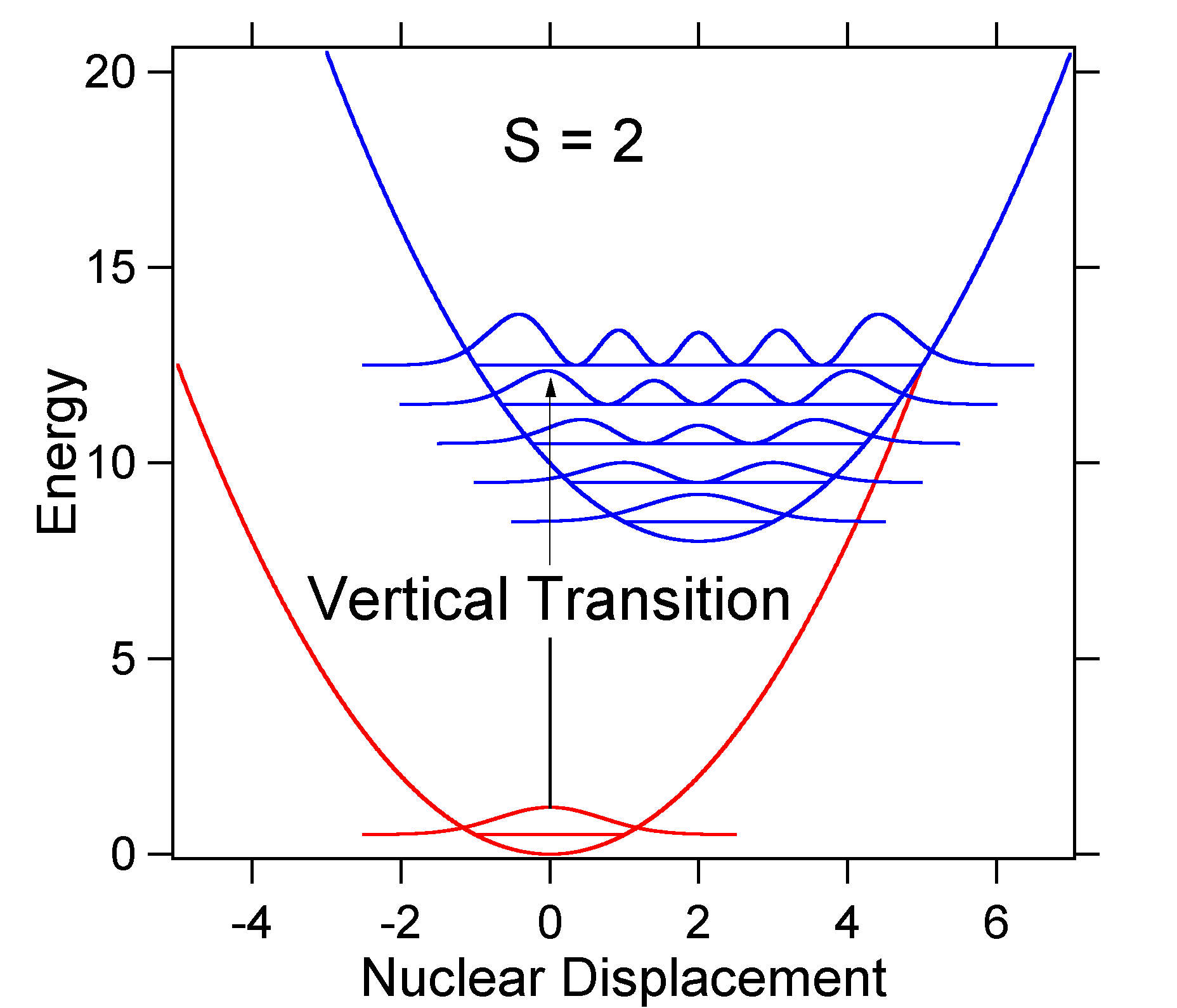
Більший зсув призводить до зменшення перекриття рівня стану землі з рівнем v = 0 збудженого стану. Максимальна інтенсивність буде досягнута при більш високих коливальних рівнях, як показано в спектрі палиці.

Рисунок Template:index: Спектр палиці, одягнений гаусами, для системи гармонічних осциляторів великого зміщення (S=2) з Figure Template:index.

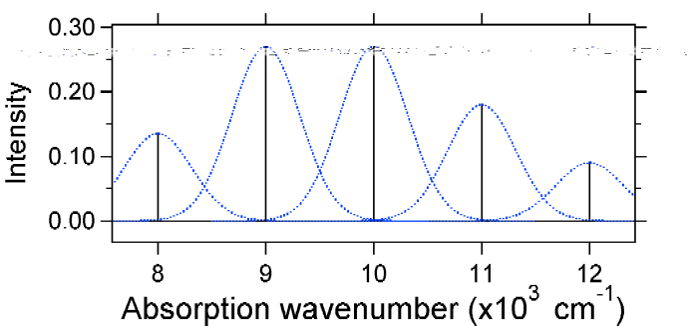
Спектри поглинання, нанесені нижче, мають однакову інтегровану інтенсивність, однак їх форми змінюються через різну ступінь зміщення збудженого стану потенційної енергетичної поверхні.

Рисунок Template:index: Спектри палиці, одягнені гаусами, для малих і великих переміщень в системі гармонічних осциляторів, описаних вище.

Тож природа відносної інтенсивності вібронічної смуги може сказати нам, чи є зміщення рівноважної ядерної координати, що супроводжувало перехід. Коли відбудеться збільшення довжини зв'язку (тобто$Q_e > R_e$)? Це відбувається, коли електрон просувається від склеювальної молекулярної орбіталі до незв'язуючої або антизв'язкової молекулярних орбіталів (тобто, коли порядок зв'язку менше в збудженому стані, ніж основний стан).

• Незв'язуючий молекулярно-орбітальний$\rightarrow$ зв'язок молекулярної орбітальної
• Молекулярна орбітальна$\rightarrow$ зв'язок проти склеювання молекулярної орбіти
• Молекулярна орбітальна$\rightarrow$ антисклеювальна молекулярна орбітальна

Коротше кажучи, коли порядок зв'язку нижче в збудженому стані, ніж у наземному стані, тоді$Q_e > R_e$; збільшення довжини зв'язку відбудеться, коли це станеться.

Посилання

1. J.M Луїс, Д.М. єпископ, Б.Кіртман. Інший підхід до обчислення факторів Франка-Кондона, включаючи ангармонічність. Дж. Хем. Фіз.С., 120 (2004), сс. 813—822.
2. Аткінс, Пітер і Хуліо де Паула. Фізична хімія для наук про життя. 2006 р. Нью-Йорк, Нью-Йорк: W.H Фрімен і компанія. стор. 563-564
3. Принцип Франка-Кондона. 1996, 68, 2243. Збірник хімічної термінології IUPAC 2-е видання (1997). www.iupac.org/Goldbook/F02510.pdf
4. Е. Рабінович і Говінджі. Поглинання світла і доля збудження енергії. 1969 р. Принцип Франка-Кондона. http://www.life.uiuc.edu/govindjee/b...em494/Abs.html