13.5: Вібраційні обертони

Last updated
Save as PDF

Page ID: 26879

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Хоча гармонічний генератор виявляється корисним при більш низьких рівнях енергії, наприклад\(v=1\), він виходить з ладу при більших числах\(v\), не тільки правильно моделювати атомні зв'язки та дисоціації, але й не в змозі відповідати спектрам, що показують додаткові лінії, ніж враховується в моделі гармонічного осцилятора.

Ангармонійність

До цього моменту ми використовували гармонічний генератор для опису міжядерної потенційної енергії коливального руху. Фундаментальні коливальні частоти молекули відповідають переходу від\(\Delta v= \pm 1\). Хоча це гідне наближення, облігації не поводяться так, як вони роблять у наближенні Гармонічний осцилятор (Рисунок Template:index). Наприклад, на відміну від параболи, наведеної в наближенні Гармонічний осцилятор, атоми, які знаходяться занадто далеко один від одного, будуть дисоціювати.

альт — Рисунок Template:index: На фото вище наведено наближення Гармонічного осцилятора (зелена парабола), накладена на ангармонічний осцилятор (синя крива) на діаграмі потенційної енергії. V (R) - потенційна енергія двоатомної молекули, а R - радіус між центрами двох атомів. До лівого - стиснення зв'язку, до правого - розширення. (CC BY-SA 3.0; Створено Марком Сомосою 26 березня 2006 р.).

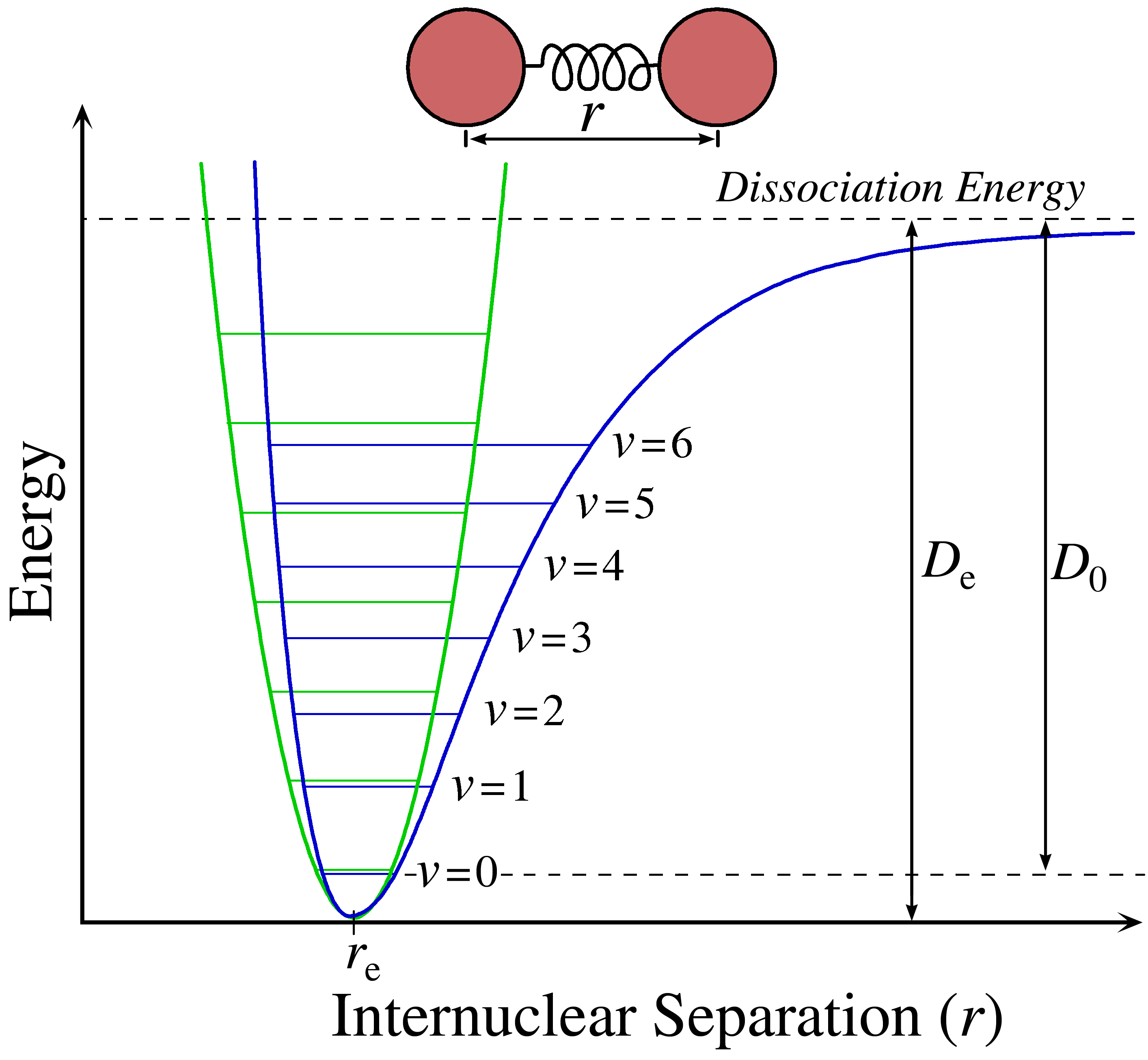
Як ви можете бачити на малюнку Template:index, потенціал гармонічного осцилятора (зеленим кольором) добре підходить лише приблизно над більш точним ангармонічним осцилятором (синім кольором). Суцільна лінія припадає на дисоціацію при великих значеннях R, які пунктирні лінії навіть віддалено не охоплюють. Однак це лише одна важлива відмінність між гармонійними та ангармонічними (реальними) осциляторами.

Реальну потенційну енергію можна розширити в серії Тейлора.

\[ V(R) = V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 + \dfrac{1}{3!}\left(\dfrac{d^3V}{dR^3}\right)_{R=R_e} (R-R_e)^3 + \dfrac{1}{4!}\left(\dfrac{d^4V}{dR^4}\right)_{R=R_e} (R-R_e)^4 + ... \label{taylor} \]

Це розширення було детально розглянуто раніше. Перший член в розширенні ігнорується, так як похідна потенціалу при\(R_e\) дорівнює нулю (тобто на дні свердловини). Наближення гармонічного осцилятора використовує лише наступний термін, квадратичний термін, у серії

\[V_{HO}(R) \approx V(R_e) + \dfrac{1}{2!}\left(\dfrac{d^2V}{dR^2}\right)_{R=R_e} (R-R_e)^2 \nonumber \]

або в терміні постійної пружини (і ігнорувати абсолютний енергетичний термін) і визначаючи\(r\) рівним зміщення від рівноваги (\(r=R-R_e\)), то отримуємо «стандартний» потенціал гармонічного осцилятора:

\[V_{HO}(R) = \dfrac {1}{2} kr^2 \nonumber \]

Крім того, розширення в рівнянні\(\ref{taylor}\) можна скоротити до кубічного члена

\[V(x) = \dfrac {1}{2} kr^2 + \dfrac {1}{6} \gamma r^3 \label{cubic} \]

де

\(V(x_0) = 0\), і\(r = R - R_0\).
\(k\)є постійною гармонійної сили, і
\(\gamma\)перший (тобто кубічний) ангармонічний термін

Важливо відзначити, що таке наближення добре тільки для\(R\) ближнього\(R_0\).

5.3.2-1.свг — Рисунок Template:index: (ліворуч) Відхилення від простого гармонічного потенціалу наближення (червона крива) істинного/точного потенціалу (синя крива) з кубічним членом (зелений). (праворуч) Розширення з позитивними або негативними квартичними термінами. (CC BY-NC; Перейти через LibreTexts)

5.3.2-2.свг — Рисунок Template:index: (ліворуч) Відхилення від простого гармонічного потенціалу наближення (червона крива) істинного/точного потенціалу (синя крива) з кубічним членом (зелений). (праворуч) Розширення з позитивними або негативними квартичними термінами. (CC BY-NC; Перейти через LibreTexts)

Гармонічний осцилятор наближення і дає наступними енергіями:

\[ E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) \nonumber \]

Коли включаються кубічні члени в розширення (Equation\(\ref{cubic}\)), тоді рівняння Шредінгера розв'язане, використовуючи теорію збурень, дає:

\[ E_{v} = \tilde{\nu} \left (v + \dfrac{1}{2} \right) - \tilde{\chi_e} \tilde{\nu} \left (v + \dfrac{1}{2} \right)^2 \nonumber \]

де\( \tilde{\chi_e}\) - константа ангармонічності. Він набагато менше 1, що має сенс, оскільки терміни в серії Тейлора наближаються до нуля. Ось чому, хоча\(G(n)\) технічно включає всі серії Тейлора, ми стосуємось лише першого та другого термінів. Решта настільки малі і ледь додають до загальної кількості і, таким чином, їх можна ігнорувати. Щоб отримати більш точне наближення, можна включити більше термінів, але в іншому випадку можна ігнорувати. Майже всі діатоміки експериментально визначені\(\frac {d^2 V}{d x^2}\) для їх найнижчих енергетичних станів. \(\ce{H2}\),\(\ce{Li2}\),\(\ce{O2}\)\(\ce{N2}\), і\(\ce{F2}\) мали терміни до\(n < 10\) визначеного рівняння\(\ref{taylor}\).

обертони

Наближення гармонічного осцилятора передбачає, що буде лише одна лінія спектру двоатомної молекули, і хоча експериментальні дані показують, що насправді є одна домінуюча лінія - фундаментальна - є також інші, слабші лінії. Як ми можемо врахувати ці додаткові рядки?

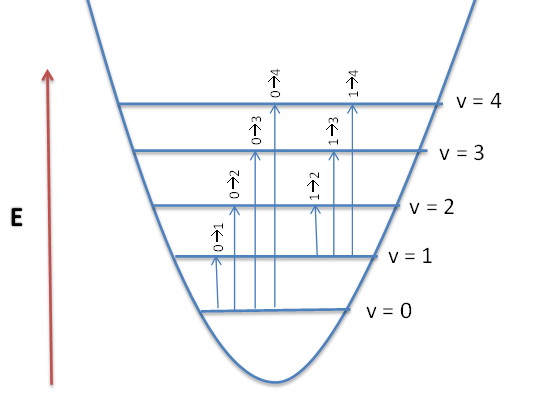
Будь-яка резонансна частота вище основної частоти називається обертоном. У ІЧ-спектрі смуги обертонів кратні основній частоті поглинання. Як ви можете згадати, рівні енергії в наближенні гармонічного осцилятора рівномірно розташовані один від одного. Енергія пропорційна поглинутій частоті, яка в свою чергу пропорційна хвильовому числу, перший обертон, який з'являється в спектрі, буде в два рази більше хвильового числа фундаментального. Тобто перший обертон\(v = 1 \rightarrow 2\) є (приблизно) вдвічі більшою енергією фундаментальної,\(v = 0 \rightarrow 1\).

Рівні не однаково розташовані, як у гармонічному осциляторі, але зменшуються зі\(v\) збільшенням, поки він в кінцевому підсумку не сходиться, мається на увазі Figure Template:index. Також в результаті ангармонії правило\(\Delta v= \pm 1\) вибору більше не діє і\(v\) може бути будь-яким числом. Це призводить до спостереження переходів вищого порядку, або обертонів, які виникають в результаті переходу основного стану на більш високі енергетичні рівні.

Правила вибору ангармонічного осцилятора

Для ангармонічного осцилятора правило вибору є\(\Delta V= \text{any number}\). Тобто немає правил вибору (для переходів від стану до стану)

Овертони виникають при порушенні коливального режиму від\(v=0\) до\(v=2\) (перший обертон) або\(v=0\) до\(v=3\) (другий обертон). Фундаментальні\(v=\pm 1\) переходи є найбільш поширеними, і ймовірність швидкого обертонів зменшується, коли\( \Delta v > \pm 1\) стає більшою. Виходячи з наближення гармонічного осцилятора, енергія переходу обертонів буде приблизно в\(v\) рази основною, пов'язаною з цим конкретним переходом. Розрахунки ангармонічного осцилятора показують, що обертони зазвичай менше, ніж кратні основній частоті. Обертони, як правило, не виявляються в більших молекулах.

Це продемонстровано коливаннями двоатомної\(\ce{HCl}\) в газовій фазі:

Таблиця Template:index: коливальний спектр HCl.
Перехід	_обс [см ^-1]	_obs Гармонічний [см ^-1]	_obs Ангармонічний [см ^-1]
\( 0 \rightarrow 1 \)(фундаментальний)	2885.9	2885.9	2 885.3
\( 0 \rightarrow 2 \)(перший обертон)	5668.0	5771.8	5 665.0
\( 0 \rightarrow 3 \)(другий обертон)	8347,0	8657,7	8 339,0
\( 0 \rightarrow 4\)(третій обертон)	10 923,1	11 543,6	10 907,4
\( 0 \rightarrow 5\)(четвертий обертон)	13 396,5	14 429,5	13 370

З таблиці Template:index видно, що ангармонічні частоти набагато краще відповідають спостережуваним частотам, особливо зі збільшенням коливальних рівнів. Оскільки енергетичні рівні та обертони ближче один до одного в ангармонічній моделі, вони також легше досягаються. Це означає, що існує більша ймовірність того, що цей рівень може бути зайнятий, тобто він може відображатися як додаткові, хоча і слабші лінії інтенсивності (слабша інтенсивність вказує на меншу ймовірність переходу).

Вправа Template:index

\(\ce{HCl}\)має основну смугу на 2885,9 см ⁻¹ і обертон на 5668,1 см ⁻¹ Обчислити\(\tilde{\nu}\) і\( \tilde{\chi_e} \).

Вправа Template:index

Випишіть серію Тейлора та прокоментуйте тенденцію у зростаючому вираженні. Використовуючи тестовий номер\(x\), будь ласка, додайте терміни 3, 4 та 5, а потім порівняйте це з терміном 2. Як вони порівнюють? Ми бачили, що ангармонічні терміни підвищують точність наближення нашого осцилятора. Чому б нам не так піклуватися про терміни, що минули другий?

Посилання

Інфрачервоний і рамановий спектри неорганічних і координаційних сполук. Частина A: Теорія та застосування в неорганічній хімії; Частина B: Застосування в координації, металоорганічної та біонеорганічної хімії, 5-е видання (Накамото, Казуо)
Лайл МакАфі Журнал хімічної освіти 2000 77 (9), 1122
Стюарт, Барбара. Інфрачервона спектроскопія: основи та застосування. Вілі, 2004. Друк.