12.4: Операції симетрії як матриці

Матриці можуть бути використані для відображення одного набору координат або функцій на інший набір. Матриці, що використовуються для цієї мети, називаються матрицями перетворення. У теорії груп ми можемо використовувати матриці перетворення для виконання різних операцій симетрії, розглянутих раніше. Як простий приклад, ми дослідимо матриці, які ми використовували б для виконання деяких з цих операцій симетрії над вектором у 2D-просторі.\(\begin{pmatrix} x, y \end{pmatrix}\).

Матриця перетворення для будь-якої операції в групі має форму, унікальну з матриць інших членів тієї ж групи; однак характер матриці перетворення для заданої операції такий же, як і для будь-якої іншої операції в тому ж класі.

Кожна операція симетрії нижче буде працювати на довільному векторі:

\[ \bf{u} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}\]

Операція ідентичності,\(E\)

Оператор ідентичності,\(E\), leaves the vector unchanged, and as you may already suspect, the appropriate matrix is the identity matrix:

\[ E\bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ z \end{pmatrix} \label{9.1} \]

Операція відображення,\(\sigma\)

Операція відображення відображає вектор\(\bf{u}\) над площиною. Це може бути\(xy\),\(xz\), або\(yz\) літак. Матриця аналогічна матриці ідентичності, за винятком того, що є зміна знака для відповідного елемента. Матриця відображення в\(xy\) площині:

\[ \sigma \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ y \\ -z \end{pmatrix} \label{9.2} \]

Зверніть увагу, що елемент для виміру відображається є на, який є негативним. У наведеному вище випадку, оскільки\(z\) відбивається над\(xy\) площиною,\(z\) елемент в матриці негативний. Якби ми повинні були відображати над\(xz\) площиною замість цього,\(y\) елемент був би негативним:

\[ \sigma \bf{u} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x \\ -y \\ z \end{pmatrix} \]

Ми також можемо говорити про роздуми у 2 вимірах. Найпростіший приклад матриці відображення відповідає відображенню вектора\(\begin{pmatrix} x, y \end{pmatrix}\) in either the \(x\) or \(y\) axes. Reflection in the \(x\) axis maps \(y\) to \(-y\), while reflection in the \(y\) axis maps \(x\) to \(-x\). The appropriate matrix is very like the identity matrix but with a change in sign for the appropriate element. Reflection in the \(x\) axis transforms the vector \(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} x, -y \end{pmatrix}\), and the appropriate matrix is

\[  \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \\ -y \end{pmatrix} \]

Рисунок Template:index: Відображення по осі x у двовимірному просторі.

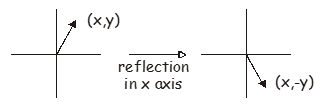
Відображення по осі y перетворює вектор\(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, y \end{pmatrix}\), and the appropriate matrix is:

\[ \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ y \end{pmatrix} \label{9.3} \]

Рисунок Template:index: Відображення по осі Y у двовимірному просторі.

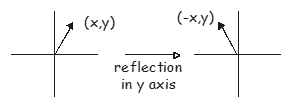
Більш загально матриці можуть використовуватися для представлення відображень у будь-якій площині (або лінії в 2D). Наприклад, відображення по осі 45°, показане під картами\(\begin{pmatrix} x, y \end{pmatrix}\) onto \(\begin{pmatrix} -y, -x \end{pmatrix}\).

\[ \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -y \\ -x \end{pmatrix} \label{9.4} \]

Рисунок Template:index: Відображення поперек осі, яка повернута на 45 ° відносно осі x у 2D-просторі.

Операція обертання\(n\) -fold,\(C_n\)

Обертання проти годинникової стрілки\(z\) приблизно:

\ [C_n\ bf {u} =\ почати {pmatrix}\ cos {\ frac {2\ pi} {n}} & -\ sin {\ frac {2\ пі} {n}} & 0\\ sin {\ frac {2\ pi} {\ frac {2\ pi} {n}} & 0\ 0 & 0 & 1\ кінець {pmatrix}\ почати {pmatrix} х
\\ y\\ z\ кінець {pmatrix} =
\ почати {pmatrix} x '\\ y'\\ z\ end {pmatrix}\]

Для обертання за годинниковою стрілкою знак на\(\sin{\theta}\) умовах буде змінений. Ця матриця значно спрощує\(C_2\) обертання:

\ [C_2\ bf {u} =\ почати {pmatrix} -1 & 0 & 0\ 0 & -1 & 0\ 0 & 0 & 0 & 1\ кінець {pmatrix}
\ почати {pmatrix} х\ y\\ z\ кінець {pmatrix} =
\ почати {pmatrix} -х\\ -y\\ z\ кінець {pmatrix}\

обертань про\(x\), \(y\) and \(z\) axes acting on a vector \(\begin{pmatrix} x, y, z \end{pmatrix}\) are represented by the following matrices.

\[R_{x}(\theta) = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix} \label{9.6a} \]

\[R_{y}(\theta) = \begin{pmatrix} \cos\theta & 0 & -\sin\theta \\ 0 & 1 & 0 \\ \sin\theta & 0 & \cos\theta \end{pmatrix} \label{9.6b} \]

\[R_{z}(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \label{9.6c} \]

Операція обертання також може виконуватися в двох вимірах. У двох вимірах відповідна матриця для представлення повороту на кут\(\theta\) щодо початку

\[R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \label{9.5} \]

Операція інверсії,\(I\)

Операція інверсії інвертує кожну точку:

\ [I\ bf {u} =\ почати {pmatrix} -1 & 0 & 0\ 0 & -1 & 0\ 0 & 0 & -1\ кінець {pmatrix}
\ почати {pmatrix} х\ y\\ z\ кінець {pmatrix} =
\ почати {pmatrix} -х\\ -y\\ -z\ кінець {pmatrix}\]

Інверсія 2D вектора\(\begin{pmatrix} x, y \end{pmatrix}\) to \(\begin{pmatrix} -x, -y \end{pmatrix}\), and the appropriate matrix is:

\[ \begin{pmatrix} -1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -x \\ -y \end{pmatrix} \]

\(C_{2v}\)Точкова група

Тепер, коли ми побачили матричну форму наших операторів, ми можемо побачити, як множення кожного оператора призводить до інших операцій в групі. Таблиця\(C_{2v}\) множення така:

\(C_{2v}\)	\(E\)	\(C_2\)	\(\sigma_v\)	\(\sigma_v'\)
\(E\)	\(E\)	\(C_2\)	\(\sigma_v\)	\(\sigma_v'\)
\(C_2\)	\(C_2\)	\(E\)	\(\sigma_v'\)	\(\sigma_v\)
\(\sigma_v\)	\(\sigma_v\)	\(\sigma_v'\)	\(E\)	\(C_2\)
\(\sigma_v'\)	\(\sigma_v'\)	\(\sigma_v\)	\(C_2\)	\(E\)

Давайте розглянемо\(C_2 \sigma_v\) множення, де\(\sigma_v\) є відображення по\(xz\) площині:

\ [C_2\ sigma_v =\ почати {pmatrix} -1 & 0 & 0\ 0 & -1 & 0\ 0 & 0 & 0 & 1\ кінець {pmatrix}\ почати {pmatrix} 1 & 0\ 0 & 0\ 0 & 0 & 0\ 1\ кінець {pmatrix}
=\ почати {pmatrix} -1 & 0\ 0\ 0 & 0\ 0\ 0\ 0\ 0\ 0\ 0\\ 0\ 0\ 0\\ 0\ 0\\ 0\ 0\\ 0\\ 0\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\ 0 & 0 & 1\ кінець {pmatrix} =\ сигма_в'\]

де\(\sigma_v'\) - відображення поперек\(yz\) площини.

Представлення матриці

Операції симетрії в групі можуть бути представлені набором матриць перетворення\(\Gamma\)\((g)\), по одній для кожного елемента симетрії\(g\). Кожна окрема матриця називається представником відповідної операції симетрії, а повний набір матриць називається матричним представленням групи. Представники матриць діють на деякому обраному базовому наборі функцій, а фактичні матриці, що складають дане уявлення, залежатимуть від обраної основи. Тоді подання, як кажуть, охоплює обрану основу. У наведених вище прикладах ми розглядали вплив деяких простих матриць перетворення на довільний вектор\(\begin{pmatrix} x, y \end{pmatrix}\). Таким чином, основою є пара одиничних векторів, що вказують в\(y\) напрямках\(x\) і. У тривимірному просторі основою є набір одиничних векторів, що вказують на\(x\)\(y\), і\(z\) напрямки. У більшості прикладів, які ми розглянемо в цьому курсі, ми будемо використовувати набори атомних орбіталів як базові функції для матричних уявлень. Перш ніж продовжувати далі, ми повинні перевірити, чи матричне представлення групи відповідає всім правилам, викладеним у формальному математичному визначенні групи.

1. Ідентичність. Перше правило полягає в тому, що група повинна включати операцію ідентичності\(E\) (операція «нічого не робити»). Вище ми показали, що матричний представник операції ідентичності - це просто матриця ідентичності. Як наслідок, кожне представлення матриці включає відповідну матрицю ідентичності.
2. Закриття. Друге правило полягає в тому, що комбінація будь-якої пари елементів також повинна бути елементом групи (властивістю group). Якщо помножити разом будь-які два представника матриці, ми повинні отримати нову матрицю, яка є представником іншої операції симетрії групи. Фактично, матричні представники розмножуються разом, щоб дати нових представників точно так само, як операції симетрії об'єднуються відповідно до таблиці множення груп. Наприклад, у\(C_{2v}\) точковій групі ми показали, що комбінована операція симетрії\(C_2\)\(\sigma_v\) еквівалентна \(\sigma_v'\). У матричному поданні групи, якщо матричні представники\(C_2\) і \(\sigma_v\)множаться разом, то результат буде представником \(\sigma_v'\).
3. Асоціативність. Третє правило говорить, що правило поєднання елементів симетрії в групі має бути асоціативним. Це автоматично задовольняється правилами множення матриць.
3. Взаємність. Заключне правило стверджує, що кожна операція повинна мати зворотну, яка також є членом групи. Комбінований ефект від проведення операції та її зворотний такий же, як і операція ідентичності. Досить легко показати, що матричні представники задовольняють цьому критерію. Наприклад, зворотне відображення - це інше відображення, ідентичне першому. Отже, у матричному терміні ми очікуємо, що матриця відображення є власною зворотною, і що дві однакові матриці відображення, помножені разом, дадуть матрицю ідентичності. Це виявляється правдою, і можна перевірити, використовуючи будь-яку з матриць відображення в прикладах вище. Обернена матриця обертання - це інша матриця обертання, що відповідає обертанню протилежного сенсу до першої.

Приклад Template:index: Матричне представлення\(C_{2v}\) Point Group (the allyl radical)

У цьому прикладі ми візьмемо за основу\(p\) orbital on each carbon atom \(\begin{pmatrix} p_1, p_2, p_3 \end{pmatrix}\).

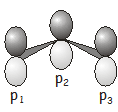
Зверніть увагу, що\(p\) orbitals are perpendicular to the plane of the carbon atoms (this may seem obvious, but if you’re visualizing the basis incorrectly it will shortly cause you a not inconsiderable amount of confusion). The symmetry operations in the \(C_{2v}\) point group, and their effect on the three \(p\) orbitals, are as follows:

\ [\ почати {масив} {ll} E &\ begin {pmatrix} p_1\\ p_2\\ p_3\ кінець {pmatrix}\ праворуч\ почати {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\\
c_2\ end {C_2\\ p_3\\ кінець {pmatrix}\ стрілка вправо\ почати {pmatrix} -p_3\\ -p_2\\ -p_1\ кінець {pmatrix}\
\ sigma_v &\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець {pmatrix}\ праворуч\ почати {pmatrix} -p_1\\ -p_2\\ -p_3\ кінець {pmatrix}\
\ sigma_v' &\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець {pmatrix}\ правий рядок\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець {pmatrix}\ кінець {масив}\ nonumber\]

Матриці, які здійснюють перетворення, є

\ [\ почати {масив} {ll}\ Гамма (E) &\ почати {pmatrix} 1 & 0\ 0 & 0\ 0 & 0\ 0 & 0 & 1\ 1\ кінець {pmatrix}\ почати {pmatrix}\ p_1\\ p_2\\ p_3\ кінець {pmatrix} =\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець {p_3\ {pmatrix}
\\ Гамма (C_2) &\ почати {pmatrix} 0 & -1\\ 0 & -1 & 0\\ -1 & 0\ кінець {pmatrix}\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець {pmatrix} =\ почати {pmatrix} -p_2\\ -p_1\ end {pmatrix}\\\
\ Гамма (\ сигма_v) і почати\ {pmatrix} -1 & 0\\ & -1 & 0\\ 0 & 0 & 0 & -1\ кінець {pmatrix}\ почати {pmatrix} p_1\\ p_2\\ p_3\ кінець { pmatrix} =\ почати {pmatrix} -p_1\\ -p_2\\ -p_3\ кінець {pmatrix}
\\ Гамма (\ сигма_v') &\ почати {pmatrix} 0 & 0 & 0\\ 1 & 0 & 0\ кінець {pmatrix}\ почати {pmatrix} p_1\\ p_2\\ p_2\\ p_3\ кінець {pmatrix} =\ почати {pmatrix} p_1\\ p_2\\ p_3\ end {pmatrix}\ кінець {масив}\ nonumber \]

Ми написали вектори, що представляють нашу основу у вигляді рядкових векторів. Це важливо. Якби ми писали їх як вектори стовпців, відповідні матриці перетворення були б транспозами матриць вище, і не відтворювали б таблицю групового множення (спробуйте це як вправу, якщо вам потрібно переконати себе).