2.3: Кінетична молекулярна теорія газів

Теоретичні моделі, які намагаються описати природу газів, датуються найбільш ранніми науковими запитами про природу речовини і навіть раніше! Приблизно в 50 році до н.е. Лукрецій, римський філософ, запропонував, щоб макроскопічні тіла були складені з атомів, які постійно стикаються один з одним і знаходяться в постійному русі, незважаючи на спостережувану реальність, що саме тіло є як спокій. Однак ідеї Лукреція значною мірою ігнорувалися, оскільки вони відхилялися від поглядів Аристотеля, погляди якого були більш широко прийняті в той час.

У 1738 році Даніель Бернуллі (Bernoulli, 1738) опублікував модель, яка містить основні рамки сучасної кінетичної молекулярної теорії. Рудольф Клаузіус продовжив модель у 1857 році, (серед іншого) запровадивши концепцію середнього вільного шляху (Клаузіус, 1857). Ці ідеї були надалі розвинені Максвеллом (Maxwell, Molecules, 1873). Але, оскільки атомна теорія не була повністю охоплена на початку ^20-го століття, лише Альберт Ейнштейн не опублікував одну зі своїх насіннєвих праць, що описує броунівський рух (Ейнштейн, 1905), в якій він моделював речовину, використовуючи кінетичну теорію молекул, що ідея атомного (або молекулярного) картина дійсно затрималася в науковому співтоваристві.

У своєму сучасному вигляді Кінетична молекулярна теорія газів заснована на п'яти основних постулатах.

1. Частинки газу підкоряються законам руху Ньютона і рухаються прямими лініями, якщо вони не стикаються з іншими частинками або стінками контейнера.
2. Частинки газу дуже малі в порівнянні з середніми показниками відстаней між ними.
3. Молекулярні зіткнення ідеально еластичні, так що кінетична енергія зберігається.
4. Частинки газу так не взаємодіють з іншими частинками хіба що через зіткнення. Між частинками відсутні привабливі або відштовхуючі сили.
5. Середня кінетична енергія частинок у зразку газу пропорційна температурі.

Якісно ця модель прогнозує форму ідеального газового закону.

1. Більше частинок означає більше зіткнень зі стіною (\(p \propto n\))
2. Менший обсяг означає більш часті зіткнення зі стіною (\(p \propto 1/V\))
3. Більш високі молекулярні швидкості означають більш часті зіткнення зі стінками (\(p \propto T\))

Складання всіх цих разом дає

\[ p \propto \dfrac{nT}{V} =k \dfrac{nT}{V}\]

який є саме формою ідеального газового закону! Решта роботи полягає в тому, щоб вивести значення для константи пропорційності (\(k\)), яка узгоджується з експериментальним спостереженням.

Для простоти уявіть собі колекцію частинок газу в контейнері з фіксованим об'ємом, де всі частинки рухаються з однаковою швидкістю. Які наслідки матиме кінетична молекулярна теорія для такого зразка? Один з підходів до відповіді на це питання полягає в тому, щоб вивести вираз для тиску газу.

Тиск буде визначатися, розглядаючи зіткнення молекул газу зі стінкою ємності. Кожне зіткнення буде надавати якусь силу. Так чим більше число зіткнень, тим більше буде тиск. Крім того, чим більша сила надається за зіткнення, тим більшим буде тиск. І нарешті, чим більше площа, по якій поширюються зіткнення, тим менше буде тиск.

\[ p \propto \dfrac{ (\text{number of collisions}) \times (\text{force imparted per collision})}{area}\]

Малюнок\(\PageIndex{1}\): «Об'єм зіткнення» - це підмножина загального об'єму, який містить молекули, які фактично зіткнуться з площею\(A\) в часовому інтервалі\(\Delta t\).

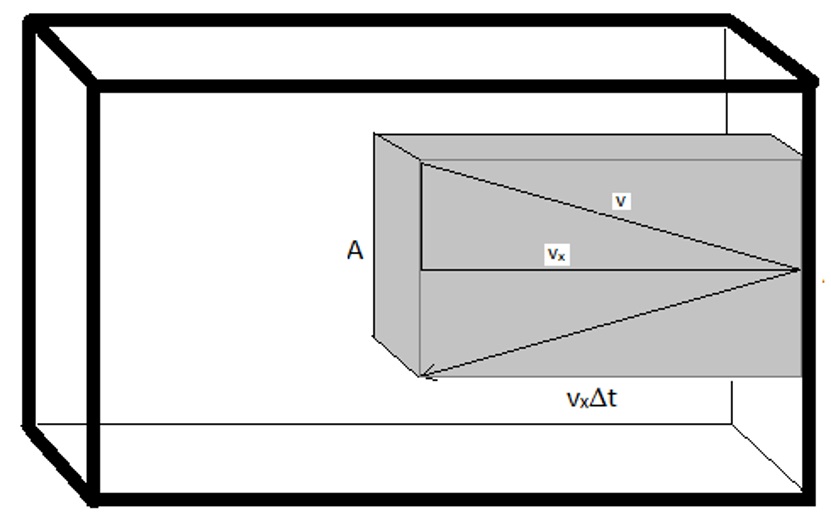
По-перше, тиск, який газ чинить на стінки контейнера, буде повністю обумовлений силою, що надається кожен раз, коли молекула стикається з внутрішньою поверхнею контейнера. Ця сила буде масштабуватися за кількістю молекул, які потрапили в область стінки за даний час. З цієї причини зручно визначати «об'єм зіткнення».

\[ V_{col}= (v_x \cdot \Delta t) \cdot A\]

де\(v_x\) - швидкість руху молекул в напрямку х,\(\Delta t\) - часовий інтервал (твір\(v_x·\Delta T\) дає довжину коробці об'єму зіткнення) і A - площа стінки, з якою молекули будуть стикатися. Половина молекул в цьому об'ємі зіткнеться зі стіною, оскільки половина буде рухатися до неї, а половина буде віддалятися від неї. Кількість молекул в цьому об'ємі зіткнення буде задаватися загальною кількістю молекул у зразку і часткою загального об'єму, який є об'ємом зіткнення. І таким чином, кількість молекул, які будуть стикатися зі стінкою, задається

\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{V_{col}}{V}\]

І таким чином кількість молекул, що зіткнулися зі стінкою, буде

\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{(v_x \cdot \Delta t) \cdot A}{V}\]

Величина цієї сили, що надається за зіткнення, буде визначатися часовою швидкістю зміни імпульсу кожної частинки, коли вона потрапляє на поверхню. Його можна розрахувати, визначивши загальну зміну імпульсу і розділивши на загальний час, необхідний для події. Оскільки кожна стикається молекула змінить свою швидкість від v _x до —v _x, величина зміни імпульсу становить 2 (mv _x). Таким чином, сила, що надається за зіткнення, задається

\[ F = \dfrac{2(mv_x)}{\Delta t}\]

і загальна сила, що надається, є

\[\begin{align} F_{tot} &= N_{col} \dfrac{2 (mv_x)}{\Delta t} \\[4pt] &= \dfrac{1}{2} N_{tot} \left[ \dfrac{(v_x\Delta t)A}{V} \right] \left[ \dfrac{2(m v_x)}{\Delta t} \right] \\[4pt] &= N_{tot} \left(\dfrac{mv_x^2}{V} \right) A \end{align}\]

Оскільки тиск задається як загальна сила, що чиниться на одиницю площі, тиск задається

\[p = \dfrac{F_{tot}}{A} = N_{tot} \left( \dfrac{mv_x^2}{V} \right) = \dfrac{N_{tot}m}{V} v_x^2\]

Тоді постає питання, як боротися з терміном швидкості. Спочатку передбачалося, що всі молекули мали однакову швидкість, і тому величина швидкості в напрямку x була лише функцією траєкторії. Однак реальні зразки газів містять молекули з цілим розподілом молекулярних швидкостей і траєкторій. Щоб розібратися з цим розподілом значень, ми замінюємо (\(v_x^2\)) на квадрат середнє значення швидкості в напрямку x\(\langle v_x \rangle ^2\).

\[p = \dfrac{N_{tot}m}{V} \langle v_x \rangle ^2 \label{press}\]

Функція розподілу швидкостей у напрямку x, відома як розподіл Максвелла-Больцмана, задається:

\[f(v_x) = \underbrace{\sqrt{ \dfrac{m}{2\pi k_BT} }}_{\text{normalization term}} \underbrace{\exp \left(\dfrac{-mv_x^2}{2k_BT} \right)}_{\text{exponential term}}\]

Ця функція має дві частини: константу нормалізації і експоненціальний термін. Константа нормалізації виводиться, зазначивши, що

\[\int _{-\infty}^{\infty} f(v_x) dv_x =1 \label{prob}\]

Нормалізація розподілу Максвелла-Больцмана

Розподіл Максвелла-Больцмана повинен бути нормалізований, оскільки це безперервний розподіл ймовірностей. Таким чином, сума ймовірностей для всіх можливих значень v _x повинна бути одиницею. І оскільки\(v_­x\) може приймати будь-яке значення між -∞ і ∞, то рівняння\ ref {prob} має бути істинним. Отже, якщо\(f(v_x)\) передбачається, що форма

\[f(v_x) = N \exp - \left(\dfrac{mv_x^2}{2k_BT} \right)\]

Постійну нормалізації\(N\) можна дізнатися з

\[ \int_{-\infty}^{\infty} f(v_x) dv_x = \int_{-\infty}^{\infty} N \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1\]

Вираз можна спростити, дозволивши\(\alpha = m/2k_BT\). Це тоді більш просто написано.

\[ N \int_{-\infty}^{\infty} \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1\]

Таблиця певних інтегралів говорить про те, що

\[ \int_{-\infty}^{\infty} e^{- a x^2} dx = \sqrt{\dfrac{\pi}{a}}\]

Так

\[ N \sqrt{\dfrac{\pi}{\alpha}} = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2}\]

І таким чином нормована функція розподілу задається

\[ f(v_x) = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \text{exp} \left( \dfrac{m v_x^2}{2 k_BT} \right) \label{MB}\]

Обчислення середнього значення за розподілом ймовірностей

Обчислити середнє значення для кінцевого набору даних досить легко. Середнє значення обчислюється по

\[ \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i\]

Але як діяти, коли набір даних нескінченний? Або як діяти, коли всі знають, чи є ймовірності для кожного можливого виміряного результату? Виявляється, що це теж досить просто!

\[ \bar{x} = \sum_{i=1}^N x_i P_i\]

де\(P_i\) - ймовірність вимірювання величини\(x_i\). Це також може бути поширене на проблеми, де вимірювані властивості не дискретні (наприклад, числа, що виникають в результаті прокатки пари кубиків), а походять від безперервної батьківської популяції. При цьому, якщо ймовірність вимірювання конкретного результату, то середнє значення потім можна визначити по

\[\bar{x} = \int x P(x) dx\]

де\(P(x)\) - функція, що описує розподіл ймовірностей, і з інтеграцією відбувається по всіх можливих значеннях, які може приймати x.

Розрахунок середнього значення\(v_x\)

Значення, яке є корисним (і буде використовуватися в подальших розробках) - це середня швидкість в напрямку x. Це можна отримати за допомогою розподілу ймовірностей, як показано у полі математичного розвитку вище. Середнє значення\(v_x\) задається

\[ \langle v_x \rangle = \int _{-\infty}^{\infty} v_x (f(v_x) dx\]

Цей інтеграл буде, за необхідністю, дорівнювати нулю. Це має бути так, оскільки розподіл симетричний, так що половина молекул рухається у напрямку +x, а половина - у напрямку —x. Ці клопоти доведеться скасувати. Отже, більш задовольняє результат буде дано при розгляді величини\(v_x\), яка дає швидкість в напрямку х. Оскільки це не може бути негативним, а з огляду на симетрію розподілу, проблема стає

\[ \langle |v_x |\rangle = 2 \int _{0}^{\infty} v_x (f(v_x) dx\]

Іншими словами, ми розглянемо лише половину розподілу, а потім подвоїмо результат, щоб врахувати половину, яку ми проігнорували.

Для простоти запишемо функцію розподілу як

\[ f(v_x) = N \exp(-\alpha v_x^2)\]

де

\[ N= \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \]

і

\[\alpha = \dfrac{m}{2k_BT}.\]

Таблиця визначених інтегралів показує

\[ \int_{0}^{\infty} x e^{- a x^2} dx = \dfrac{1}{2a}\]

тому

\[ \langle v_x \rangle = 2N \left( \dfrac{1}{2\alpha}\right) = \dfrac{N}{\alpha}\]

Підставляючи наші визначення\(N\) і\(\alpha\) виробляє

\[ \langle v_x \rangle = \left( \dfrac{m}{2\pi k_BT} \right)^{1/2} \left( \dfrac{2 k_BT}{m} \right) = \left( \dfrac{2\pi k_BT}{ \pi m} \right)^{1/2} \]

Цей вислів вказує на середню швидкість руху в одному напрямку.

Однак реальні зразки газу мають молекули не тільки з розподілом молекулярних швидкостей, а й випадковим розподілом напрямків. Використовуючи властивості нормальної величини вектора (або просто використовуючи теорему Піфагора), видно, що

\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2\]

Оскільки напрямок руху є випадковим, швидкість може мати будь-яку складову в напрямках x, y або z з однаковою ймовірністю. Таким чином, середнє значення x, y або z складових швидкості має бути однаковим. І так

\[ \langle v \rangle^2 = 3 \langle v_x \rangle^2\]

Підставляючи це у вираз для тиску (Equation\ ref {press}) дає

\[ p =\dfrac{ N_{tot}m}{3V} \langle v \rangle^2\]

Залишається лише визначити форму розподілу швидкісних величин, які можуть приймати молекули газу. Одним з перших людей, які звернулися до цього розподілу, був Джеймс Клерк Максвелл (1831-1879). У своїй роботі 1860 р. (Максвелл, Ілюстрації динамічної теорії газів. Частина 1. Про рухи та зіткнення ідеально пружних сфер, 1860 р.) запропоновано форму такого розподілу швидкостей, яка виявилася узгодженою із спостережуваними властивостями газів (такими як їх в'язкість). Він вивів цей вираз на основі перетворення системи координат з декартових координат (\(x\),\(y\),\(z\)) до сферичних полярних координат (\(v\),\(\theta\),\(\phi\)). У цій новій системі координат v представляє величину швидкості (або швидкості), і всі дані спрямованості переносяться в кутах\(\theta\) і\(\phi\). Нескінченно мала одиниця об'єму стає

\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi\]

Застосування цього перетворення координат і ігнорування кутової частини (так як його цікавила тільки швидкість) розподіл Максвелла (Equation\ ref {MB}) прийняв наступний вигляд

\[ f(v) = N v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFullN}\]

Ця функція має три основні частини: константу нормалізації (\(N\)), залежність від швидкості (\(v^2\)) та експоненціальний термін, який містить кінетичну енергію (\(½ mv^2\)). Оскільки функція являє собою частку молекул зі швидкістю\(v\), сума дробів для всіх можливих швидкостей повинна бути одиницею. Цю суму можна обчислити як інтеграл. Константа нормалізації гарантує, що

\[ \int_0^{\infty} f(v) dv = 1\]

Вибір константи нормалізації як

\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 }\]

дає остаточну форму розподілу Максвелла молекулярних швидкостей.

\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFull}\]

При низьких швидкостях\(v^2\) термін змушує функцію збільшуватися зі збільшенням\(v\), але потім при більших\(v\) значеннях експоненціальний термін змушує його знижуватися асимптотично до нуля. Розподіл буде поширюватися в більшому діапазоні швидкостей при більш високих температурах, але руйнується до меншого діапазону значень при більш низьких температурах (табл. 2.3.1).

Малюнок 2.3.1: Розподіл Максвелла швидкостей для молекул водню при різних температурах.

Розрахунок середньої швидкості

Використовуючи розподіл Максвелла як розподіл ймовірностей, можна визначити середню молекулярну швидкість у зразку молекул газу.

\[ \begin{align} \langle v \rangle & = \int _{-\infty}^{\infty} v \,f(v) dv \\ & = \int _{-\infty}^{\infty} v\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^3 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align}\]

У таблиці інтегралів можна знайти наступне:

\[ \int_0^{\infty} x^{2n+1} e^{-ax^2} dx = \dfrac{n!}{2a^{n+1}}\]

Так

\[\langle v \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1}{2 \left( \dfrac{m}{2 k_B T} \right) ^2 } \right]\]

Що спрощує

\[\langle v \rangle = \left( \dfrac{8 k_BT}{\pi m} \right) ^{1/2} \]

Примітка: значення\(\langle v \rangle \) в два рази більше, ніж було виведено в попередньому прикладі!\(\langle v_x \rangle \)

\[\langle v \rangle = 2\langle v_x \rangle \]

Приклад\(\PageIndex{1}\):

Яке середнє значення швидкості в квадраті згідно із законом розподілу Максвелла?

Рішення:

\[ \begin{align} \langle v^2 \rangle & = \int _{-\infty}^{\infty} v^2 \,f(v) dv \\ & = \int _{-\infty}^{\infty} v^2\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^4 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align}\]

Таблиця інтегралів вказує на те, що

\[ \int_0^{\infty} x^{2n} e^{-ax^2} dx = \dfrac{1 \cdot 3 \,cdot 5 \dots (2n-1)}{2^{n+1}a^n} \sqrt{\dfrac{\pi}{a}}\]

Заміна (зазначивши, що\(n = 2\)) врожайність

\[\langle v^2 \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1 \cdot 3}{2^3 \left( \dfrac{m}{2 k_BT} \right) ^2 } \sqrt{\dfrac{\pi}{\left( \dfrac{m}{2 k_BT} \right)}} \right]\]

що спрощує

\[\langle v^2 \rangle = \dfrac{3 k_BT}{ m} \]

Примітка: Квадратний корінь цієї середньої квадратної швидкості називається середньоквадратичною швидкістю (RMS) і має значення

\[v_{rms} = \sqrt{ \langle v^2 \rangle } = \left( \dfrac{3 k_BT}{ m} \right)^{1/2}\]

На весь розподіл впливає і молекулярна маса. Для більш легких молекул розподіл поширюється в більш широкому діапазоні швидкостей при заданій температурі, але руйнується в меншому діапазоні для більш важких молекул (табл. 2.3.2).

Малюнок 2.3.2: Розподіл Максвелла швидкостей при 800 К для різних газів різної молекулярної маси.

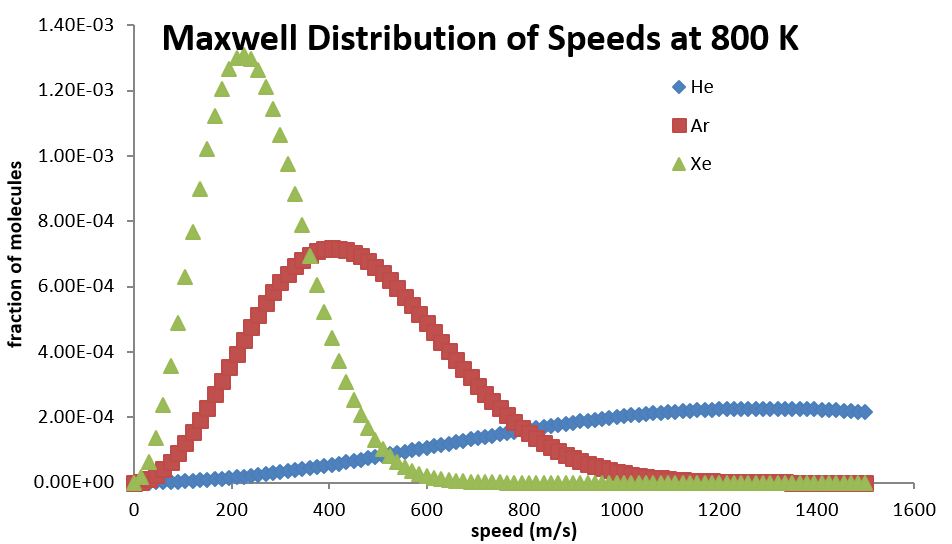
Функція розподілу ймовірностей також може бути використана для отримання виразу для найбільш ймовірної швидкості (\(v_{mp}\)\(v_{ave}\)), середньої () та середньоквадратичної (\(v_{rms}\)) швидкостей як функції температури та маси молекул у зразку. Найімовірніша швидкість - та з максимальною ймовірністю. Це буде швидкість, яка дає максимальне значення\(f(v)\). Він знаходить, вирішуючи вираз

\[ \dfrac{d}{dv} f(v) = 0\]

за цінність\(v\) того, що робить це правдою. Це буде величина, яка дає максимальне значення\(f(v)\) для даної температури. Аналогічно, середнє значення можна знайти за допомогою розподілу наступним чином

\[ v_{ave} = \langle v \rangle \]

і середньоквадратичної (середньоквадратичної) швидкості шляхом знаходження квадратного кореня середнього значення\(v^2\). Обидва продемонстровані вище.

\[ v_{rms} = \sqrt{ \langle v^2 \rangle} \]