1.5: Робота та енергія

Температура, тиск і об'єм є важливими змінними в описі фізичних систем. Вони також будуть важливі для опису того, як енергія перетікає з однієї системи в іншу. Як правило, енергія може протікати в двох важливих формах: 1) робота і 2) тепло. Бухгалтерія, необхідна для відстеження потоку енергії, - це те, що стосується термодинаміки, тому ці теми будуть детально розглянуті в наступних розділах. Однак трохи рецензії є для того, щоб просто закласти основу для майбутніх дискусій.

Енергія

Енергетика є важливою сутністю в сучасному світі. Ми використовуємо енергію для освітлення наших будинків, керування нашими автомобілями та живлення наших електронних пристроїв. За словами Річарда Смоллі, співлауреата Нобелівської премії 1996 року з хімії, енергія є одним з (якщо не найбільший) виклик, з яким ми стикаємося, рухаючись у ^21-му столітті (energy.senate.gov, 2004):

Енергія лежить в основі практично кожної проблеми, з якою стикається людство. Ми не можемо дозволити собі помилитися... Якимось чином ми повинні знайти основу для енергетичного процвітання для себе та решти людства на XXI століття. До середини цього століття ми повинні припустити, що нам потрібно буде принаймні подвоїти світове виробництво енергії від його нинішнього рівня, причому більша частина цього надходить від якогось чистого, стійкого, вільного від CO ₂ джерела. Для миру та процвітання у всьому світі він повинен бути дешевим.- Річард Смоллі, Свідчення Комітету Сенату з питань енергетики та природних ресурсів, 26 квітня 2004 р.

Енергія може вимірюватися в безлічі різних одиниць, включаючи джоулі (J), кілоджоулі (кДж), калорії (кал), кілокалорії (ккал), а також кілька інших наборів одиниць, таких як кДж/моль або ккал/моль.

Калорійність (кал) колись була визначена як кількість енергії, необхідної для підвищення температури 1 г води на 1 °С, це визначення передбачає зручну властивість води, яка називається питомою теплотою:

\[C = \dfrac{1\,cal}{g\, °C}\]

Сучасне визначення калорії - 4,184 джоуля,

\[ 1 \,J = 1\,N \cdot m = \dfrac{1 \,kg \, m^2}{s^2}\]

де джоуль - енергія, необхідна для переміщення маси на відстань 1 м проти сили опору 1 Н.

Дієтична калорійність (Кал) дорівнює 1000 кал, або 1 ккал, і часто вказана на етикетках харчових контейнерів для позначення енергетичної вмісту їжі всередині.

Енергія може приймати форму потенційної енергії (накопиченої енергії) і кінетичної енергії (реалізованої енергії) форм. Кінетична енергія - це енергія руху. З іншого боку, потенційну енергію можна визначити як енергію, що зберігається в системі, яка може бути перетворена в кінетичну енергію десь у Всесвіті. Кінетична енергія частинки може бути виражена у вигляді

\[E_{kin} = \dfrac{1}{2} mv^2 \label{transKE}\]

де\(m\) - маса частки, і\(v\) - величина її швидкості (або швидкості). Рівняння\ ref {TransKe} описує кінетичну енергію, пов'язану з перекладом; інші вирази існують для різних рухів (наприклад, обертання або вібрації).

Прикладом системи, в якій енергія перетворюється між кінетичною енергією та потенційною енергією, є генератор закону Гука. Згідно із Законом Гука, сила, що діє на об'єкт, пропорційна за величиною зміщенню об'єкта з положення рівноваги, і протилежна за знаком.

\[ F = -kx \label{hook}\]

У цьому рівнянні,\(F\) є сила,\(x\) є зміщення від рівноваги, і\(k\) є константою пропорційності. Негативний знак необхідний для того, щоб гарантувати, що сила, що діє на об'єкт, є тією, яка буде прагнути відновити його до положення рівноваги (\(x = 0\)) незалежно від того, позитивна чи\(x\) негативна.

Коли об'єкт, який слідує Закону Гука, рухається з положення рівноваги, кінетична енергія його руху перетворюється в потенційну енергію, поки не залишиться більше кінетичної енергії. У цей момент зміна зміщення змінить напрямок, повертаючи об'єкт в положення рівноваги шляхом перетворення потенційної енергії назад в кінетичну енергію.

Малюнок 1.5.1: Приклад гармонічного осцилятора.

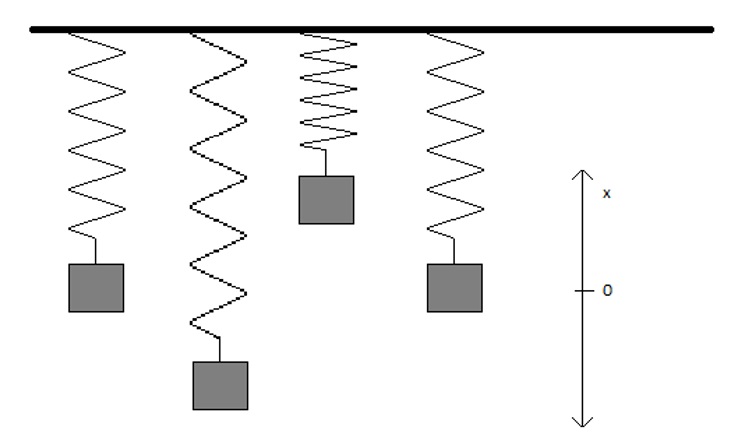
У міру зміщення об'єкта вздовж осі x (у випадку, показаному на малюнку 1.5.1, це було б досягнуто шляхом розтягування або стиснення пружини) потенційна енергія збільшується. Сила, що діє на об'єкт, також буде збільшуватися при зміщенні об'єкта і буде спрямована навпроти напрямку переміщення (Equation\ ref {hook}). Згідно з ньютонівською фізикою, потенційна енергія\(U(x)\) задається негативним інтегралом сили щодо положення:

\[U (x) = - \int F(x) dx \label{energy}\]

Підстановка рівняння\ ref {хук} у рівнянні\ ref {energy} дає

\[U(x) = - \int (-k x)dx\]

\[ = \dfrac{1}{2} kx^2 + constant\]

При правильному виборі системи координат та інших визначень константу інтеграції можна довільно зробити нульовою (наприклад, вибравши її для зміщення будь-яких інших сил, що діють на об'єкт, наприклад, сили, обумовленої гравітацією). Кінетична енергія потім дається повною енергією мінус потенційна енергія (оскільки загальна енергія повинна бути постійною через збереження енергії в системі!)

\[ E_{kin} = E_{tot} -U(x)\]

Робота

Робота визначається як кількість енергії, витраченої на переміщення маси проти сили опору. Для маси, що рухається вздовж поверхні, кількість витраченої енергії повинна бути достатньою для подолання сили опору (можливо, через тертя), а також достатньою для сприяння руху по всьому шляху.

Малюнок 1.5.2: Робота зміщення.

Енергія, витрачена в якості роботи в цьому випадку (якщо сила не залежить від положення переміщається об'єкта) дається

\[w= - F \,\Delta x\]

де F - величина сили опору, а D x - зміщення об'єкта. Негативний знак необхідний, так як сила діє в протилежному напрямку руху. Більш загальний вираз, і той, який можна використовувати, якщо сила не є постійною протягом усього руху, є

\[ dw = -F \,dx\]

Цей вираз може бути інтегрований, включаючи будь-яку залежність, яка\(F\) може мати від необхідної для даної системи.\(x\)

Ще один важливий спосіб, який можна визначити роботу, включає розширення зразка газу проти зовнішнього тиску. При цьому зміщення визначається зміною обсягу для зразка:

\[dw = -p_{ext} dV\]

Це дуже зручний вислів і буде використовуватися досить часто при обговоренні роботи, витраченої на розширення газу.

Перетворення потенційної енергії в кінетичну енергію, як правило, здійснюється за допомогою роботи, яка виконується десь у Всесвіті. Як такі поняття енергії і роботи невблаганно переплітаються. Вони займуть центральне місце у вивченні термодинаміки.

Робота «оборотного» розширення

Важливим випадком обмеження ідеальної поведінки [1] є оборотне розширення. Щоб зміна була оборотною, не може бути чистої сили, що штовхає зміну в тому чи іншому напрямку. Для того, щоб це було так, внутрішній тиск (тиск системи) та зовнішній тиск (тиск оточення) повинні бути однаковими.

\[p_{int} = p_{ext} = p\]

При цьому роботу розширення можна обчислити, інтегруючи вираз для dw.

\[w = \int dw = -\int p dV\]

Робимо просту заміну з ідеального закону газу

\[p=\dfrac{nRT}{V} \label{IGL}\]

дозволяє вираження за обсягом і температурою. Якщо температура постійна (щоб її можна було поставити перед інтегралом) вираз стає

\[w= - nRT \int_{V_1}^{V_2} \dfrac{dV}{V} = -nRT \ln \left( \dfrac{V_2}{V_1} \right) \label{workIG}\]

де\(V_1\) і\(V_2\) є початковим і кінцевим обсягами розширення відповідно.

Приклад\(\PageIndex{1}\):

Розглянемо 1,00 моль ідеального газу, що розширюється ізотермічно при 273 К, від початкового об'єму 11,2 л до кінцевого обсягу 22,4 л. Що таке кінцевий тиск газу? Розрахуйте роботу розширення, якщо воно відбувається

1. проти постійного зовнішнього тиску, рівного кінцевому тиску, який ви розрахували.
2. оборотно.

Рішення:

Спочатку розрахуємо кінцевий тиск за допомогою Equation\ ref {IGL}:

\[ p = \dfrac{nRT}{V} = \dfrac{(1.00\,mole)(0.08206\, atm\,L\,mol^{-1} K^{-1})(273\,K)}{22.4\, L} = 1.00 \, atm\]

(Це може бути зв'язок, який ви пам'ятаєте із загальної хімії - що 1 моль ідеального газу займає 22,4 л при 0 ^o C!)

Гаразд — тепер для незворотного розширення проти постійного зовнішнього тиску:

\[dw = -p_{ext}dV\]

тому

\[w = -p_{exp} \int _{V_1}^{V_2} dV = -p_{ext} \Delta V\]

\[ w = -(1.00 \, atm)(22.4 \, L- 11.2\,L) =-11.2 \,atm\,L\]

Але що за біса це атм L? Це насправді досить проста річ, щоб перетворити з одиниць атм L в J за допомогою ідеальної константи закону газу.

\[w = -(11.2 \,atm\,L) \left( \dfrac{8.314\, \frac{J}{mol\, K}}{0.08206\, \frac{atm\, L}{mol\, K}} \right) = -11.30 \,J\]

Зверніть увагу, що негативний знак вказував на те, що система витрачає енергію, виконуючи роботу над оточенням. (Ця концепція буде життєво важливою в главі 3!)

Тепер про оборотний шлях. Роботу, виконану системою, можна обчислити для цієї зміни за допомогою Equation\ ref {WorkiG}:

\[w= -(1.00\, mol) (8.314 J\, mol^{-1} K^{-1}) (273 \,K) \ln \left( \dfrac{22.4\,L}{11.2\,L} \right) = -1570\,J\]

Примітки:

• Спочатку зверніть увагу, як значення константи закону газу, R, було обрано для того, щоб відповідати одиницям, необхідним у задачі. (Прочитайте і декламуйте це попереднє речення собі кілька разів. Неправильний вибір значення R - одна з найпоширеніших помилок, допущених учнями фізичної хімії! Дізнавшись, як одиниці будуть диктувати ваш вибір R, ви заощадите собі значну кількість головних болів, коли ви вивчаєте фізичну хімію!)
• По-друге, Ви можете відзначити, що величина роботи, виконаної системою в реверсивному розширенні, більше, ніж у незворотного розширення. Так буде завжди!

---

[1] Існує багато випадків «обмеження ідеальної поведінки», які ми використовуємо для отримання та/або вивчення природи хімічних систем. Найбільш очевидним випадком, мабуть, є Закон про ідеальний газ.