4.6: Теорія збурень залежної від часу
- Page ID
- 18888
При роботі з ефектами зовнішніх збурень (наприклад, прикладних полів, зіткнень з іншими видами) потрібно мати спосіб оцінки ймовірностей і швидкостей переходів між станами системи інтересів, індукованих цими збуреннями. Зазалежна від часу теорія збурень (TDPT) пропонує рамки, в яких такі оцінки можуть бути досягнуті.
деривація
При отриманні робочих рівнянь TDPT починається з залежного від часу рівняння Шредінгера
\[i\hbar \frac{\partial \Psi}{\partial t}=[H_0+V(t)]\Psi \label{1}\]
в якому\(H_0\) є гамільтоном для системи, переходи якої повинні бути досліджені, і\(V(t)\) є збуренням, викликаним зовнішнім полем або зіткненням. Хвильова функція, яка вирішує це рівняння, розширюється в порядку порядку, як у звичайній теорії збурень
\[\Psi=\psi^{(0)}(r)\exp\Big(-it\frac{E^{(0)}}{\hbar}\Big)+\psi^{(1)}+\cdots \label{2}\]
\(\psi_0\)Ось своя функція,\(H_0\) від якої розглядаються переходи в інші власні стани (\(H_0\)позначаються). Оскільки, за відсутності зовнішнього збурень, стани\(V(t)\), як відомо,\(H_0\) змінюються з часом, оскільки ця складова часової залежності загальної хвильової функції включена в вищезгадане розширення. Потім корекція першого порядку\(\psi^{(1)}\) розширюється за рахунок повної множини станів {}, після чого коефіцієнти розширення {} стають невідомими для розв'язання
\[\psi^{(1)}=\sum_f \psi^{(0)}_f(r)\exp\bigg(-it\frac{E^{(0)}_f}{\hbar}\bigg)C^{(1)}_f(t). \label{3}\]
Слід зазначити, що ця деривація розглядає стани нульового порядку {\(\psi^{(0)}\)і\(\psi^{(0)}_f\)} як власні функції\(H_0\). Однак у більшості практичних застосувань TDPT {\(\psi^{(0)}\)і\(\psi^{(0)}_f\)} точно не відомі і, по суті, зазвичай наближаються за допомогою варіаційних або збуренних методів (наприклад, для лікування відмінностей між середнім полем ВЧ і справжніми куломбічними взаємодіями між електронами). Отже, виведення TDPT, яке ми переслідуємо, передбачає, що {\(\psi^{(0)}\)і\(\psi^{(0)}_f\)} є точними власними функціями. Коли таким чином отримані кінцеві робочі рівняння ТДПТ, зазвичай підставляють збурені або варіаційні наближення до {\(\psi^{(0)}\)і\(\psi^{(0)}_f\)} в ці рівняння.
Підставляючи розширення порядку за порядком у рівняння Шредінгера, для лівої та правої сторін,
\ [i\ hbar\ frac {\ частковий\ Psi} {\ частковий t} = E^ {(0)}\ psi^ {(0)} (r)\ exp\ Великий (-it\ frac {E^ {(0)}} {\ hbar}\ великий)\\
+\ sum_f\ лівий [E^ {(0)} _f\ psi^ {(0)} _f (r)\ exp\ bigg (-it\ frac {E^ {(0)} _f} {\ бар}\ великий) C^ {(1)} _f (t)
-i\ бар\ псі^ {(0)} _f (r)\ exp\ великий (-це\ frac {E^ {(0)} _f} {\ hбар}\ великий)\ розрив {C^ {(1)} _f (t)} {dt}\ право]\ мітка {4a}\]
і
\ [[H_0+V (t)]\ Псі = Е^ {(0)}\ psi^ {(0)} (r)\ exp\ Великий (-це\ frac {E^ {(0)}} {\ hbar}\ великий)\\\
sum_f E^ {(0)} _f\ psi^ {(0)} _f (0)} _f (r)\ exp\ великий (-це\ frac {E^ {(0)} _f} {\ hbar}\ великий) C^ {(1)} _f (t)
+V (t)\ psi^ {(0)} (r)\ exp\ великий (-це\ frac {E^ {(0)}} {\ бар}\ великий),\ етикетка {4b}\]
відповідно, через першого порядку. Множення кожного з цих рівнянь зліва на комплексний сполучений конкретний\(\psi_f^0\) та інтегрування над змінними, що\(H_0\) залежить від, дає наступне рівняння для невідомих коефіцієнтів першого порядку:
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}_f \rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{5}\]
Стани і можуть бути різними електронними станами, коливальними станами або обертальними станами. У розділі 15 моєї книги «Квантова механіка в хімії», про яку йдеться в главі 1, я детально розглядаю кожен із цих типів переходів. У цій дискусії я обмежуся загальною картиною TDPT, а не зосереджуюся на будь-якій з цих конкретних форм спектроскопічних переходів.
Щоб продовжити далі, потрібно щось сказати про те, як\(V(t)\) залежить збуреність від часу. У найбільш поширеному застосуванні TDPT передбачається, що збуреність складається з терміна, який залежить від просторових змінних (позначаються\(v(r)\)), помножених на залежний від часу коефіцієнт синусоїдального характеру. Приклад такого збурень наводиться електричним дипольним потенціалом.
\[V(t)=\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\cos(\omega t)\]
характеризують фотони частоти, що\(\omega\) взаємодіють з ядрами і електронами молекули. \(\textbf{E}\cdot [ e\sum_n Z_n \textbf{R}_n - e \sum_i \textbf{r}_i ]\)є просторовою частиною\(v(\textbf{r})\) і\(\cos(\omega t)\) є залежністю від часу.
Щоб забезпечити можливість того, що фотони в діапазоні частот можуть впливати на молекули, ми можемо приступити до виведення фотонів заданої\(\omega\) частоти і, отримавши наш кінцевий результат, усереднити розподіл частот, що характеризується функцією,\(f(\omega)\) що дає кількість фотонів з частотами між\(\omega\) і\(\omega+d\omega\). Для збурень, які не змінюються синусоїдальним способом (наприклад, збуренням, що виникає внаслідок зіткнення з іншою молекулою), похідне відбувається іншим шляхом у цій точці (додаток 3 нижче). Оскільки спектроскопічні залежні від часу збурень надзвичайно поширені в хімії, ми зосередимо більшу частину нашої уваги на цьому класі збурень у цій главі.
Щоб продовжити виведення робочих рівнянь TDPT, вищевказаний вираз для\(V(t)\) вставляється в диференціальне рівняння для коефіцієнтів розширення, і рівняння інтегрується від початкового часу\(t_i\) до кінцевого часу\(t_f\). Ці часи описують, коли зовнішнє збурення вперше включається і коли воно відключено відповідно. Наприклад, лазер, чий профіль інтенсивності фотонів описується\(f(\omega)\) може бути імпульсний від\(t_i\) до\(t_f\), і хтось хоче знати, яка частка молекул спочатку в\(\psi_0\) зазнали переходів до кожного з. Крім того, молекули можуть протікати в потоці, який проходить через лазерне джерело світла, який постійно включений, потрапляючи в лазерний промінь\(t_i\) і виходячи з лазерного променя в\(t_f\). У будь-якому випадку молекули будуть піддаватися впливу фотонів з\(t_i\) до\(t_f\). Результат інтегрування диференціального рівняння
\ [\ почати {спліт} C^ {(1)} _f (t) &=\ розрив {-1} {2i\ hbar}\ int_ {t_i} ^ {t_f}\ ланголь\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон
[\ exp (я\ омега т) +\ exp (-i\ омега т)]\ exp\ bigg (-це\ frac {(E^ {(0)} -Е^ {(0)} _f)} {\ hbar}\ bigg)\\
&=\ frac {-1} {2i\ hbar}\ int_ {t_i} ^ {t_f}\ лангл\ psi^ {0)} _f|v (r) |\ псі^ {(0)} _f (r)\ діапазон
[\ exp (i (\ омега+\ омега_ {f,0}) t) +\ exp (-i (\ омега-\ омега_ {f,0}) t)]\
&=\ frac {-1} {2i\ hbar}\ лангель\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон\\
&\ раз\ ліворуч [\ frac {\ exp (i (\ омега+\ омега_ {f,0}) t_f-\ exp (i (\ омега+\ омега_ {f,0}) t_i))} {i (\ омега+\ омега_ {f,0}))} {i (\ омега+\ омега_ {f,0} })}
+\ frac {\ exp (-i (\ омега-\ омега_ {f,0}) t_f-\ exp (-i (\ омега-\ омега_ {f,0}) t_i))} {i (\ омега-\ омега_ {f,0})}
\ праворуч]\ кінець {спліт}\ етикетка {6}\]
де частоти переходу\(\omega_{f,0}\) визначаються
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar} \label{7}\]
і\(t\) є часовим інтервалом\(t_f –t_i\).
Тепер, якщо частота\(\omega\) близька до однієї з частот переходу, термін з\((\omega-\omega_{f,0})\) в знаменнику буде більше, ніж термін, що містить\((\omega-\omega_{f,0})\). Звичайно, якщо має більш високу енергію, ніж, тому вивчає стимулювати емісійну спектроскопію,\(\omega_{f,0}\) буде негативним, і в цьому випадку термін, що містить,\((\omega+\omega_{f,0})\) буде домінувати. В умовах он-резонансної абсорбційної спектроскопії вищевказаний вираз для коефіцієнтів першого порядку зводиться до
\ [C^ {(1)} _f (t) =\ frac {-1} {2i\ hбар}\ ланголь\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон\ frac {
\ exp (-i (\ омега-\ омега_ {f,0}) _f (r)\ діапазон\ frac {\ exp (-i (\ омега-\ омега_ {f,0}) t_i))} {i (\ омега-\ омега_ {f,0})}. \ етикетка {8}\]
Модуль пружності в квадраті цієї величини дає міру ймовірності спостереження системи в стані після того, як її піддавали фотонам частоти\(\omega\) протягом певного часу\(t\).
\ [|C^ {(1)} _f (t) |^2=\ розрив {|\ ланголь\ псі^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон|^2} {4\ hbar ^ 2}
\ frac {2 [1-\ cos (\ омега-\ омега_ {f,0}) t)]} {(\ омега-\ омега_ {f,0}) ^2}\\
=\ розрив {|\ ланголь\ псі ^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон|^2} {4\ hbar ^ 2}\ frac {\ sin^2 (1/2 (\ омега-\ омега_ {f,0}) т)} {(\ омега-\ омега_ {f,0}) ^2}
. \ етикетка {9}\]
Функція\(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) побудована на малюнку 4.4 для заданого значення\(t\) як функції\(\omega\). Він різко досяг максимуму навколо\(\omega = \omega_{f,0}\), швидко розпадається зі\(|(\omega - \omega_{f,0})|\) збільшенням, і відображає рецидиви меншої та меншої інтенсивності, коли\((\omega - \omega_{f,0})t\) проходить через кратні\(\pi\).
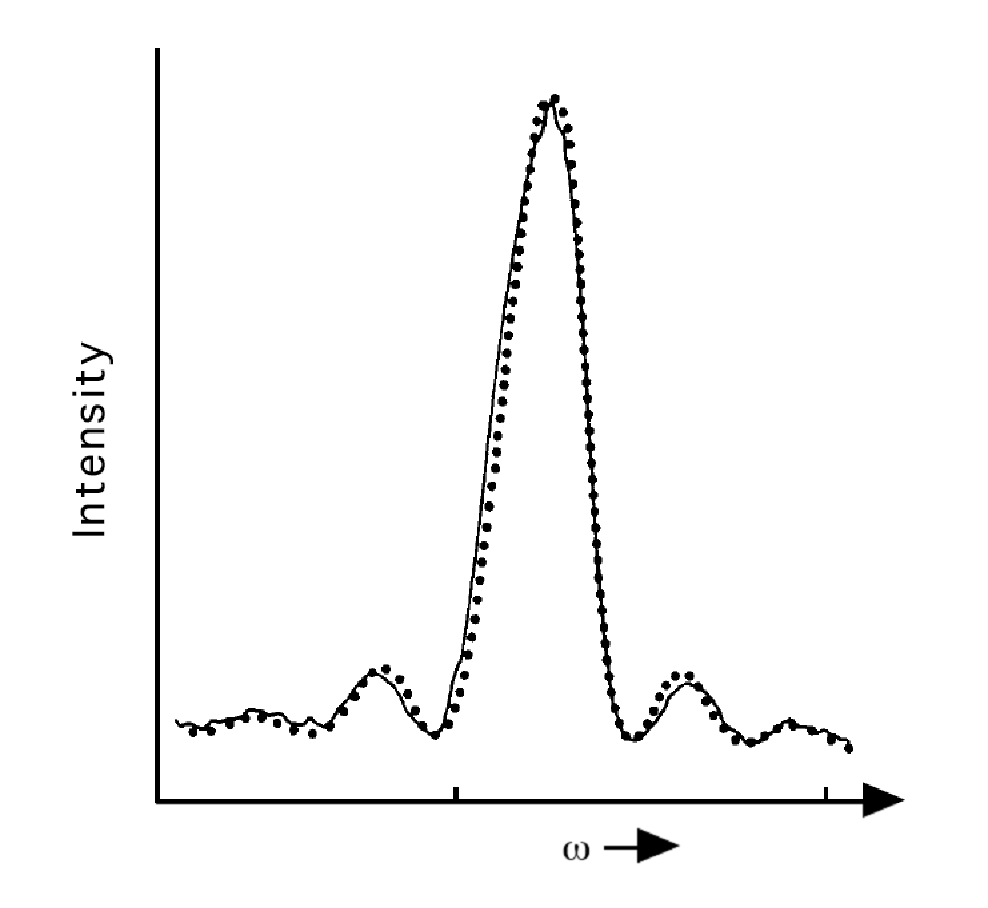
При більших значеннях\(t\), основний пік на графіку цієї функції стає більш вузьким і вищим таким, що в\(t \rightarrow \infty\) межі площа під цією ділянкою наближається\(t\pi/2\):
\[{\rm Area}=\int\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}d\omega=t\frac{\pi}{2}. \label{10}\]
Важливість цього спостереження про площі під сюжетом, показаним на малюнку 4.4, можна оцінити, повернувшись до нашого результату.
\[|C^{(1)}_f(t)|^2= \frac{|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2} \frac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2} \label{11}\]
і введення того факту, що джерело фотонів, що використовується для індукування досліджуваних переходів, швидше за все, не зовсім однотонний. Якщо він характеризується, як було запропоновано раніше, розподілом частот,\(f(\omega)\) який є ширшим, ніж ширина великого центрального піку на малюнку 4.4 (n.b., це буде вірно, якщо тривалість часу\(t\) досить велика), то, коли ми усереднюємо більше,\(f(\omega)\) щоб отримати результат, який безпосередньо відноситься до такого роду експерименту, отримуємо
\ [\ int_ {-\ infty} ^\ infty f (\ омега) |C^ {(1)} _f (t) |^2d\ омега
=\ frac {|\ ланґль\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон|^2} {4\ hbar^2}\ int_ {-\ infty} ^\ infty f (\ омега)\ frac {\ sin^2 (1/2 (\ омега-\ омега_ {f,0}) t)} {(\ омега-\ омега_ {f,0}) ^2} д\ омега\\
\ фрак {\ pi|\ лангель\ psi^ {(0)} _f|v (r) |\ psi^ {(0)} _f ( r)\ діапазон |^2t} {4\ hbar ^ 2} f (\ omega_ {f,0}) =\ лангове |C^ {(1)} _f (t) |^2\ діапазон
\ мітка {12}\]
Нам дозволено писати інтеграл, починаючи від\(-\infty\) до\(\omega\),\(+\infty\) тому що функція, показана на малюнку 4.4, настільки різко досягла максимуму,\(\omega_{f,0}\) що розширення діапазону інтеграції не має ніякого значення. Нам дозволяється фактор\(f(\omega)\) виходу з інтеграла як f (\(\omega_{f,0}\)), припускаючи, що функція\(f(\omega)\) розподілу джерела світла дуже плавно змінюється (тобто не сильно змінюється) у вузькому діапазоні частот навколо,\(\omega_{f,0}\) де функція на малюнку 4.4 різко досягла максимуму.
Результатом такого виведення TDPT є вищевказаний вираз для середньої ймовірності спостереження переходу від стану\(\psi_0\) до стану. Видно, що ця ймовірність лінійно зростає з тривалістю часу, протягом якого система піддається впливу джерела світла. Оскільки ми проводили цю деривацію в теорії збурень першого порядку, ми повинні довіряти цьому результату лише в умовах, коли ефекти збурень невеликі. У контексті розглянутого тут прикладу це означає лише короткий час. Тобто ми повинні розглядати
\[\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2t}{4\hbar^2}f(\omega_{f,0})=\langle |C^{(1)}_f(t)|^2 \rangle \label{13}\]
як виражає короткочасну оцінку ймовірності переходу від\(\psi_0\) до і
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\]
(отримано як\(\dfrac{d\langle |C^{(1)}_f(t)|^2 \rangle}{dt}\)) як вираження початкової швидкості таких переходів в межах наближення TDPT першого порядку.
Слід зазначити, що вираз швидкості, наведене вище, не буде дійсним, якщо тривалість часу t збурень не підкоряється\(\omega_{f,o} t \gg p\); тільки коли ця умова виконана і функція, показана на малюнку 4.4, буде інтегрована для створення прогнозу ймовірності, яке зростає лінійно з часом. Отже, потрібно бути обережним при використанні імпульсних лазерів дуже короткої тривалості, щоб не використовувати спрощене вираження швидкості, наведене вище (наприклад, 1 еВ відповідає частоті приблизно 2.4 x10 14 с -1, тому для вивчення електронного переходу цієї енергії потрібно використовувати джерело світла тривалість значно більше, ніж\(10^{-14}\) s, щоб скористатися спрощеним результатом).
Робочі рівняння ТДПТ, наведені вище, дозволяють оцінити (оскільки це теорія першого порядку) швидкості переходів з одного квантового стану в інший, індукованих збуренням, просторова залежність якого характеризується\(v(r)\) і чия залежність від часу синусоїдальна. Той самий вид елементів матриці зв'язку,\(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) як ми відчували в незалежних від часу PT регулюють правила вибору та інтенсивності для цих переходів, тому немає необхідності повторювати, як симетрія може бути використана для аналізу цих інтегралів.
Перш ніж закрити це лікування ТДПТ, корисно вирішити кілька питань, які були обійти при виведенні, представленому вище.
Застосування 1: Зчеплення з континуумом
У деяких випадках цікавить переходи з певного початкового стану\(\psi^{(0)}(r)\) в різноманіття станів, які існують в континуумі, що мають енергії між\(E^{(0)}_f\) і\(E^{(0)}_f+dE^{(0)}_f\). Це відбувається, наприклад, при лікуванні фотоіонізації нейтралі або фотовідшарування аніона; тут викинутий електрон існує в хвильовій функції континууму, щільність станів якої\(\rho(E^{(0)}_f)\) задається формулами, розглянутими в главі 2. У таких випадках вираз, наведений вище для швидкості, модифікується шляхом підсумовування всіх кінцевих станів, що мають енергії всередині\(E^{(0)}_f\) і\(E^{(0)}_f+dE^{(0)}_f\). Повернення до попереднього виразу
\ [\ int\ rho (E^ {(0)} _f)\ frac {\ pi |\ ланголь\ псі^ {(0)} _f|v (r) |\ psi^ {(0)} _f (r)\ діапазон|^2} {4\ hbar^2}
\ int_ {-\ infty} ^\ інфти} (\ омега)\ frac {\ sin^2 (1/2 (\ омега-\ омега_ {f,0}) t)} {(\ омега-\ омега_ {f,0}) ^2} д\ омега де^ {(0)} _f\ етикетка {14}\]
використовуючи\( dE^{(0)}_f=\hbar\omega_{f,0}\), і припускаючи, що елементи матриці\(\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle\) не суттєво змінюються у вузькому діапазоні між і, один приходить з вираженням швидкості
\[{\rm Rate}=\frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,0})\rho(E^{(0)}_f) \label{15}\]
який так само, як ми отримали раніше, але тепер містить щільність станів\(\rho(E^{(0)}_f)\). У деяких експериментах може не бути тільки єдиного стану,\(\psi^{(0)}_f(r)\) здатного поглинати світло заданої частоти w; в такій ситуації загасання джерела світла на цій частоті може відбуватися через поглинання з багатьох початкових станів\(\psi^{(0)}_f(r)\) у всі можливі кінцеві стани, енергія яких відрізняється від що початкового стану по. При цьому правильне вираз для сумарної швидкості поглинання фотонів енергії виходить усереднення вищевказаного результату над ймовірностями\(P_i\) знаходження системи в різних початкових станах (які ми позначаємо\(\psi^{(0)}_i\)):
\[{\rm Rate}=\sum_i P_i \frac{\pi|\langle \psi^{(0)}_f|v(r)|\psi^{(0)}_f(r)\rangle|^2}{4\hbar^2}f(\omega_{f,i})\rho(E^{(0)}_f)\delta(\omega-\omega_{f,i}). \label{16}\]
Тут\(\delta(\omega-\omega_{f,i})\) функція гарантує, що в суму дозволяється вводити тільки держави\(\psi^{(0)}_i\) і енергії\(\psi^{(0)}_f\) яких відрізняються. Характер ймовірності початкового стану\(P_i\) залежить від того, який саме експеримент проводиться. \(P_i\)може бути розподілом Больцмана, якщо початкові стани знаходяться в тепловій рівновазі, наприклад.
Застосування 2: Експериментальні коливання
На малюнку 4.4 функція\(\dfrac{\sin^2(1/2(\omega-\omega_{f,0})t)}{(\omega-\omega_{f,0})^2}\) побудована для одного значення\(t\) як функції\(\omega\). На цьому малюнку також з'являються точки, які представляють експериментальні дані. Ці дані були отримані, дозволяючи потоку\(HCN\) молекул протікати через лазерний промінь ширини\(L\) з налаштуванням частоти лазера\(\omega\). За швидкістю\(v\) потоку\(HCN\) потоку і ширині лазерного променя можна визначити тривалість\(L\), протягом якої молекули піддавалися впливу джерела світла\(t = \dfrac{L}{v}\). Після того як молекули вийшли з лазерного променя, їх промацували, щоб визначити, чи знаходяться вони в збудженому стані. Цей експеримент повторювався для різних значень частоти\(\omega\). Потім популяція збуджених станів була побудована як функція\(\omega\) отримання даних, побудованих на малюнку 4.4. Цей експеримент описаний у тексті Молекули та випромінювання, Дж. Штайнфельд, MIT Press, Кембридж, Массачусетс (1981). Цей експеримент дав прямий доказ коливальної частотної залежності, що спостерігається в популяції збуджених станів, як це передбачалося при нашому виведенні ТДПТ.
Застосування 3: Зіткнення індукованих переходів
Щоб навести приклад того, як протікає в ТДПТ, коли збурень не є коливальним за часом, розглянемо атом, розташований біля початку нашої системи координат, який відчуває зіткнення з іоном заряду c, траєкторія якого описана на малюнку 4.5.
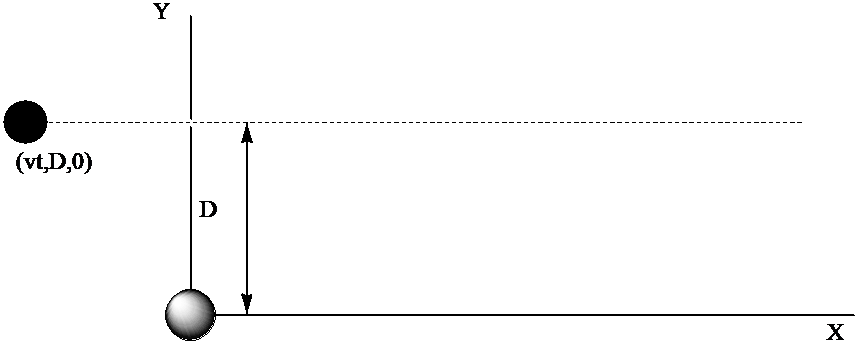
Як наближення припускаємо
- що іон рухається по прямій лінії:\(= vt, Y = D, Z = 0\), характеризується параметром удару\(D\) і швидкістю\(v\) (це було б доречно, якби іон рухався настільки швидко, що він не відхилявся б взаємодіями з атомом),
- що збурень, викликане іоном на електрони атома біля початку, може бути представлено
\[-\sum_{i=1}^N\frac{\chi}{|\textbf{r}_i-\textbf{R}|} \label{17}\]
де\(\textbf{r}_i\) - положення i-го електрона в атомі і\(\textbf{R} = (vt, D, 0)\) - положення іона. Часова залежність збурень виникає від руху іона уздовж\(X\) -осі.
Запис відстані\(|\textbf{r}_i-\textbf{R}|\) як
\[|\textbf{r}_i-\textbf{R}|=\sqrt{(x_i-vt)^2+(y_i-D)^2+z_i^2} \label{18}\]
і розширюючись у обернених потужностях,\(\sqrt{D^2+(vt)^2}\) ми можемо висловити потенціал взаємодії іон-атомів як
\[-\sum_{i=1}^N\frac{\chi}{|r_i-R|}=\sum_i^N\left[\frac{-\chi}{\sqrt{D^2+(vt)^2}}+\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}+\cdots\right]. \label{19}\]
Перший термін не містить факторів, залежних від електронних координат атома, тому він не грає ніякої ролі у викликанні електронних переходів. У другому семестрі фактором\(r_i^2\) можна знехтувати\(vtx_i+Dy_i\) порівняно з термінами, оскільки іон вважається дещо віддаленим від валентних електронів атома.
Щоб вивести рівняння ймовірності того, що атом зазнає перехід від\(\psi^{(0)}(r)\) до\(\psi^{(0)}_f(r)\), повертається до виразу TDPT
\[-i\hbar\frac{dC^{(1)}_f(t)}{dt}=\langle \psi^{(0)}_f|V(t)|\psi^{(0)}(r)\rangle\exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg) \label{20}\]
і підставляє вищевказаний вираз для збурень для отримання
\[\frac{dC^{(1)}_f(t)}{dt}=\frac{-1}{i\hbar} \langle \psi^{(0)}_f|\sum_{i=1}^N \frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle \exp\bigg(-it\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg). \label{21}\]
Це рівняння, яке необхідно вирішити для оцінки шляхом інтеграції від\(t = -\infty\) до\(t = +\infty\) (представляє повне зіткнення з іоном, що починається далеко ліворуч на\(X\) -осі і йде далеко вправо).
Є два обмежувальних випадки, в яких рішення є простим. По-перше, якщо тривалість часу зіткнення (тобто час, протягом якого іон близький до атома)\(\dfrac{D}{v}\) довга в порівнянні з\(\omega_{f,I}\) де
\[\omega_{f,0}=\frac{(E^{(0)}-E^{(0)}_f)}{\hbar}, \label{22}\]
то ціле число буде коливатися неодноразово протягом часу, в\(\dfrac{D}{v}\) результаті чого інтеграл
\[C^{(1)}_f(t)=\int_{-\infty}^\infty \frac{dC^{(1)}_f(t)}{dt}dt \label{23}\]
буде зникаючим маленьким. Так, в цьому так званому адіабатичному випадку (тобто при повільному переміщенні іона щодо частоти коливань\(\omega_{f,0}\)) електронних переходів очікувати не варто. В іншій межі\(\omega_{f,0}\dfrac{D}{v} \ll 1\) коефіцієнт\(\exp\bigg(-it\dfrac{(E^{(0)}-E^{(0)}_f)}{\hbar}\bigg)\) залишиться приблизно рівним єдності, тому необхідна інтеграція зводиться до
\[C^{(1)}_f(t)=\frac{-1}{i\hbar}\int_{-\infty}^\infty\langle\psi^{(0)}_f|\frac{-\chi(vtx_i+Dy_i+r_i^2)}{(D^2+(vt)^2)^{3/2}}|\psi^{(0)}(r)\rangle dt. \label{24}\]
Інтеграл за участю\(vtx_i\)\(vt\) зникає, тому що є непарним, а решта integrand є парною функцією\(t\). Інтеграл за участю\(Dy_i\) може виконуватися шляхом тригонометричної підстановки (\(vt = D \tan\theta\)так знаменник зводиться до\(D^3 \Big(1+\Big(\dfrac{\sin\theta}{\cos\theta}\Big)^2\Big)^{3/2} = \dfrac{D^3}{(\cos\theta)^3}\) і дає
\[C^{(1)}_f(t)=\frac{-2\chi}{i\hbar\nu D}\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle. \label{25}\]
Такий результат говорить про те, що ймовірність переходу
\[|C^{(1)}_f(t)|^2=\frac{4\chi^2}{\hbar^2\nu^2 D^2}|\langle\psi^{(0)}_f|\sum_{i=1}^N y_i|\psi^{(0)}(r)\rangle|^2. \label{26}\]
повинні змінюватися як квадрат заряду іона, так і обернено зі швидкістю зіткнення. Звичайно, такому результату не можна довіряти, якщо швидкість\(v\) занадто низька тому, то умова не\(\omega_{f,0}\dfrac{D}{v} \ll 1\) буде триматися. Цей приклад показує, як потрібно повторно виводити рівняння TDPT при роботі з збуреннями, залежність від часу яких не є синусоїдальною.
Посилання
Для читача, який бажає більш повне і різноманітне лікування TDPT, як застосовується до хімії, я пропоную текст Радіація і шум в квантовій електроніці, WH H. Louisell, R.E. Krieger, Pub., Хантінгтон, Н.Ю. (1977), а також мій текст Квантова механіка в хімії.
